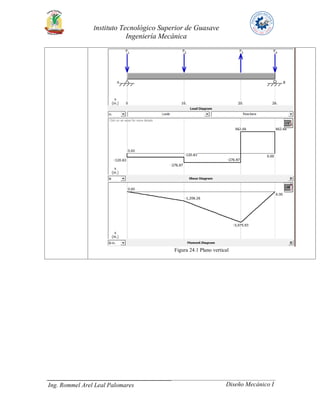
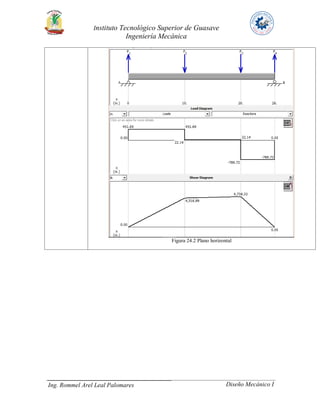
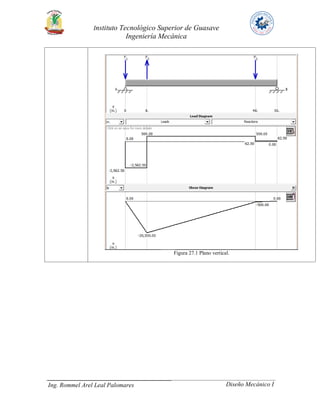
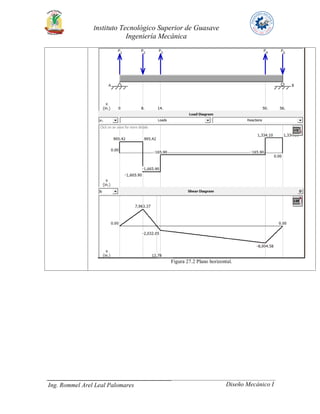
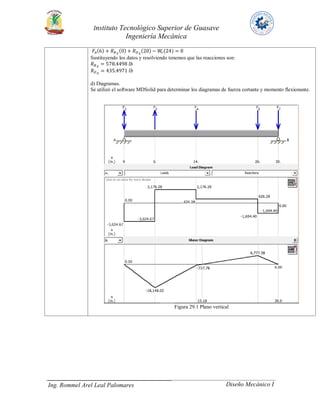
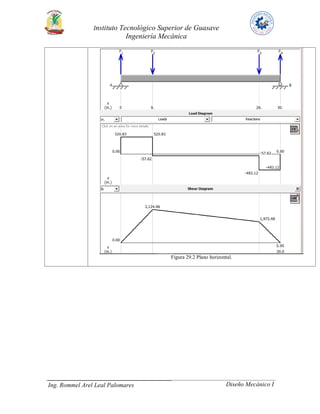
El documento presenta tres problemas de diseño de ejes. En el problema 24, se analiza un eje que transmite 30 HP a través de un engrane y una polea. En el problema 27, se analiza un eje que transmite 40 HP a un engrane y dos catarinas. En ambos problemas se calculan los pares torsionales, fuerzas en los elementos de transmisión, reacciones en los cojinetes y diagramas de carga. El objetivo es determinar los diámetros mínimos para resistir las cargas de manera segura.

1. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
Diseño Mecánico I
Tema IV. Ejes
Ejercicios extra clase: Problemas de diseño de ejes.
Nombre del estudiante: Perea Urías María Isabel Grupo: 601 Matrícula: 1625010403
Objetivo: Analizar y resolver problemas relacionados con los esfuerzos en los ejes sometidos a cargas estáticas
y dinámicas.
Instrucciones:
Resuelve los ejercicios 24, 27 y 29 del Capítulo 12 Diseño de ejes de la bibliografía de Mott, Robert; “Diseño
de Elementos de Máquinas”.
En cada uno de los problemas será necesario realizar lo siguiente:
a) Determine la magnitud del par torsional en el eje en todos los puntos.
b) Calcule las fuerzas que actúan sobre el eje en todos los elementos de transmisión de potencia.
c) Calcule las reacciones en los cojinetes.
d) Trace los diagramas completos de carga, fuerza cortante y momento flexionante.
Ignore el peso de los elementos en los ejes, a menos que
se indique lo contrario.
El objetivo de cada problema sería:
*Diseñar el eje completo, incluyendo la especificación de la geometría en general y la consideración de
factores de concentración de esfuerzos. El análisis indicaría el diámetro mínimo aceptable en cada punto
del eje, para que sea seguro desde el punto de vista de resistencia.
Nota: Puede utilizar MDSolid para determinar los diagramas de fuerza cortante y momento flexionante.
24 El eje de la figura P12-1 es parte de una transmisión para un sistema de transferencia automática en una
planta de estampado de metal. El engrane Q entrega 30 HP al engrane B. La polea D entrega la potencia a
su polea acoplada, como se indica. El eje que sostiene a B y D gira a 550 rpm. Use acero AISI 1040 estirado
en frío.
Figura P12-1. Problema 24

2. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
Objetivo Diseñar el eje completo, incluyendo la especificación de la geometría en general y la consideración de
factores de concentración de esfuerzos. El análisis indicaría el diámetro mínimo aceptable en cada punto
del eje, para que sea seguro desde el punto de vista de resistencia.
Datos 𝑃 = 30 𝐻𝑃
𝑛 = 550 𝑟𝑝𝑚
𝑠 𝑢 = 80 𝑘𝑠𝑖
𝑠 𝑦 = 71 𝑘𝑠𝑖
Tablas y/o
gráficas
Apéndice 3. Propiedades de diseño para los aceros al carbón y aleados.
Figura 5-8 Resistencia a la fatiga en función de la resistencia a la tensión, para el acero forjado con varias
condiciones de superficie.
Tabla 5-1 Factores de confiabilidad aproximados.
Figura 5-9 Factor por tamaño.
Fórmulas 𝑆´ 𝑛 = 𝑠 𝑛 𝐶𝑠 𝐶 𝑅
𝑇 =
63000 𝑃
𝑛
𝑊𝑡 = 𝑇/(𝐷/2)
𝑊𝑟 = 𝑊𝑡 𝑡𝑎𝑛Φ
𝐹 𝑁 = 𝐹1 − 𝐹2 = 𝑇/(𝐷/2)
𝐹 𝐷 = 1.5𝐹 𝑁
Operaciones
matemáticas,
diagramas y/o
dibujos y/o
representaciones
gráficas y
resultados
Primero se determinan las propiedades del acero para el eje. Del apéndice 3 AISI 1040 acero estirado en
frío, 𝑠 𝑢 = 80 𝑘𝑠𝑖, 𝑠 𝑦 = 71 𝑘𝑠𝑖 y el porcentaje de elongación es de 12%. Entonces el material tiene buena
ductilidad.
a) Par torsional.
De la figura 5-8 se puede estimar que 𝑠 𝑛 = 30 𝑘𝑠𝑖.
Se debe aplicar un factor por tamaño a la resistencia de fatiga, el diámetro estimado es 𝐷 = 5 𝑖𝑛, entonces
𝐶𝑠 = 0.859 − 0.02125(5) = 0.75275.
También se debe especificar un factor de confiabilidad aproximado de la tabla 5-1. Para este problema, se
diseñará con una confiabilidad de 0.99 y se anejará 𝐶 𝑅 = 0.81. Ya se puede calcular la resistencia a la fatiga
modificada.
𝑆´ 𝑛 = 𝑠 𝑛 𝐶𝑠 𝐶 𝑅 = (30 000)(0.75275)(0.81) = 18 291.825 𝑝𝑠𝑖
Se supondrá un factor de diseño de 𝑁 = 2.
Ahora se pasa a calcular el par torsional en el eje, con la ecuación:
𝑇 =
63000 𝑃
𝑛
=
63000 (30 𝐻𝑃)
(550 𝑟𝑝𝑚)
= 3 436.3636 𝑙𝑏 ∙ 𝑝𝑢𝑙𝑔
b) Fuerzas sobre los engranes. Engranes rectos (Q impulsa a B).
La fuerza tangencial se obtiene con la ecuación:
𝑊𝑡 =
𝑇
𝐷
2
=
3 436.3636 𝑙𝑏 ∙ 𝑝𝑢𝑙𝑔
16 𝑝𝑢𝑙𝑔
2
= 429.5454 𝑙𝑏 ←
La fuerza radial se obtiene mediante la ecuación:
𝑊𝑟 = 𝑊𝑡 𝑡𝑎𝑛Φ = (429.5454 𝑙𝑏)tan(20°) = 156.3417 𝑙𝑏 ↓
Fuerza para bandas V (polea D)

3. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
La fuerza impulsora neta se obtiene mediante la ecuación:
𝐹 𝑁 = 𝐹1 − 𝐹2 =
3 436.3636 𝑙𝑏 ∙ 𝑝𝑢𝑙𝑔
10 𝑝𝑢𝑙𝑔
2
= 687.2727 𝑙𝑏
La fuerza flexionante sobre el eje para transmisiones con bandas V se obtiene:
𝐹 𝐷 = 1.5𝐹 𝑁 = 1.5(687.2727 𝑙𝑏) = 1 030.9090 𝑙𝑏
La fuerza de flexión actúa hacia abajo y hacia la derecha formando un ángulo de 40° con la horizontal.
Como se ve en la figura P12-1, los componentes de la fuerza flexionante son:
𝐹 𝐷 𝑥
= 𝐹 𝐷 𝐶𝑜𝑠 40° = (1 030.9090 𝑙𝑏) 𝐶𝑜𝑠 40° = 789.7221 𝑙𝑏 →
𝐹 𝐷 𝑦
= 𝐹 𝐷 𝑆𝑒𝑛 40° = (1 030.9090 𝑙𝑏) 𝑆𝑖𝑛 40° = 662.6555 𝑙𝑏 ↓
c) Reacciones es los cojinetes.
Mediante las ecuaciones de estática determinamos las reacciones de los cojinetes.
Plano vertical:
∑ 𝐹𝑦 = 0
𝐹𝐴 + 𝐹𝐶 𝑦
− 𝑊𝑟 − 𝐹 𝐷 𝑦
= 0
∑ 𝑀𝐴 = 0
𝐹𝐴(0) + 𝐹𝐶 𝑦
(20) − 𝑊𝑟(10) − 𝐹 𝐷 𝑦
(26) = 0
Sustituyendo los datos y resolviendo tenemos que las reacciones son:
𝐹𝐶 𝑦
= 939.622 𝑙𝑏
𝐹𝐴 = −120.626 𝑙𝑏
Plano horizontal:
∑ 𝐹𝑥 = 0
𝐹𝐴 − 𝑊𝑡 − 𝐹𝐶 𝑥
+ 𝐹 𝐷 𝑥
= 0
∑ 𝑀𝐴 = 0
𝐹𝐴(0) − 𝑊𝑡(10) − 𝐹𝐶 𝑥
(20) + 𝐹 𝐷 𝑦
(26) = 0
Sustituyendo los datos y resolviendo tenemos que las reacciones son:
𝐹𝐶 𝑥
= 811.8659 𝑙𝑏
𝐹𝐴 = 451.6893 𝑙𝑏
d) Diagramas.
Se utilizó el software MDSolid para determinar los diagramas de fuerza cortante y momento flexionante.

4. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
Figura 24.1 Plano vertical

5. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
Figura 24.2 Plano horizontal

6. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
27 El eje de la figura P12-4 impulsa un transportador grande, de material a granel. El engrane recibe 40 HP y
gira a 120 rpm. Cada catarina entrega 20 HP a un lado del transportador. Use acero AISI 1020 estirado en
frío.
Figura P12-4. Problema 27
Objetivo Diseñar el eje completo, incluyendo la especificación de la geometría en general y la consideración de
factores de concentración de esfuerzos. El análisis indicaría el diámetro mínimo aceptable en cada punto
del eje, para que sea seguro desde el punto de vista de resistencia.
Datos 𝑃 = 40 𝐻𝑃
𝑛 = 120 𝑟𝑝𝑚
𝑠 𝑢 = 61 𝑘𝑠𝑖
𝑠 𝑦 = 51 𝑘𝑠𝑖
Tablas y/o
gráficas
Apéndice 3. Propiedades de diseño para los aceros al carbón y aleados.
Figura 5-8 Resistencia a la fatiga en función de la resistencia a la tensión, para el acero forjado con varias
condiciones de superficie.
Tabla 5-1 Factores de confiabilidad aproximados.
Figura 5-9 Factor por tamaño.
Fórmulas 𝑆´ 𝑛 = 𝑠 𝑛 𝐶𝑠 𝐶 𝑅
𝑇 =
63000 𝑃
𝑛
𝑊𝑡 = 𝑇/(𝐷/2)
𝑊𝑟 = 𝑊𝑡 𝑡𝑎𝑛Φ
𝐹𝐶 =
𝑇
𝐷
2
Operaciones
matemáticas,
diagramas y/o
dibujos y/o
representaciones
gráficas y
resultados
Primero se determinan las propiedades del acero para el eje. Del apéndice 3 AISI 1020 acero estirado en
frío, 𝑠 𝑢 = 61 𝑘𝑠𝑖, 𝑠 𝑦 = 51 𝑘𝑠𝑖 y el porcentaje de elongación es de 15%. Entonces el material tiene buena
ductilidad.
a) Par torsional.
De la figura 5-8 se puede estimar que 𝑠 𝑛 = 22 𝑘𝑠𝑖.
Se debe aplicar un factor por tamaño a la resistencia de fatiga, el diámetro estimado es 𝐷 = 6 𝑖𝑛, entonces
𝐶𝑠 = 0.859 − 0.02125(6) = 0.7315.
También se debe especificar un factor de confiabilidad aproximado de la tabla 5-1. Para este problema, se
diseñará con una confiabilidad de 0.99 y se anejará 𝐶 𝑅 = 0.81. Ya se puede calcular la resistencia a la fatiga
modificada.
𝑆´ 𝑛 = 𝑠 𝑛 𝐶𝑠 𝐶 𝑅 = (22 000)(0.7315)(0.81) = 13 035.33 𝑝𝑠𝑖
Se supondrá un factor de diseño de 𝑁 = 2.

7. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
Ahora se pasa a calcular el par torsional en el eje, con la ecuación:
𝑇 =
63000 𝑃
𝑛
=
63000 (40 𝐻𝑃)
(120 𝑟𝑝𝑚)
= 21 000 𝑙𝑏 ∙ 𝑝𝑢𝑙𝑔
Cada Catarina entrega 20 HP de potencia, entonces el par torsional de las catarinas es:
𝑇 =
63000 𝑃
𝑛
=
63000 (20 𝐻𝑃)
(120 𝑟𝑝𝑚)
= 10 500 𝑙𝑏 ∙ 𝑝𝑢𝑙𝑔
b) Fuerzas sobre los engranes. Engranes rectos (P impulsa a A).
La fuerza tangencial se obtiene con la ecuación:
𝑊𝑡 =
𝑇
𝐷
2
=
21 000 𝑙𝑏 ∙ 𝑝𝑢𝑙𝑔
16 𝑝𝑢𝑙𝑔
2
= 2 625 𝑙𝑏 ↓
La fuerza radial se obtiene mediante la ecuación:
𝑊𝑟 = 𝑊𝑡 𝑡𝑎𝑛Φ = (2 625 𝑙𝑏 𝑙𝑏) tan(20°) = 955.4218 𝑙𝑏 →
Fuerzas en las cadenas:
𝐹𝐶 =
𝑇
𝐷
2
=
10 500 𝑙𝑏 ∙ 𝑝𝑢𝑙𝑔
14 𝑝𝑢𝑙𝑔
2
= 1 500 𝑙𝑏 →
c) Reacciones es los cojinetes.
Mediante las ecuaciones de estática determinamos las reacciones de los cojinetes.
Plano vertical:
∑ 𝐹𝑦 = 0
−𝑊𝑡 + 𝑅 𝐵 𝑦
+ 𝑅 𝐸 𝑦
= 0
∑ 𝑀 𝐵 = 0
−𝑊𝑡(8) + 𝑅 𝐵 𝑦
(0) − 𝑅 𝐸 𝑦
(48) = 0
Sustituyendo los datos y resolviendo tenemos que las reacciones son:
𝑅 𝐸 𝑦
= −437.5 𝑙𝑏
𝑅 𝐵 𝑦
= 3 062.5 𝑙𝑏
Plano horizontal:
∑ 𝐹𝑥 = 0
𝑊𝑟 + 𝐹𝐶 𝐶
+ 𝐹𝐶 𝐷
− 𝑅 𝐵 𝑥
− 𝑅 𝐸 𝑥
= 0
∑ 𝑀 𝐸 = 0
𝑊𝑟(56 𝑖𝑛) + 𝐹𝐶 𝐶
(42) + 𝐹𝐶 𝐷
(6) − 𝑅 𝐵 𝑥
(48) − 𝑅 𝐸 𝑥
(0) = 0
Sustituyendo los datos y resolviendo tenemos que las reacciones son:
𝑅 𝐵 𝑥
= 2 661.3254 𝑙𝑏
𝑅 𝐸 𝑥
= 1 334.0964 𝑙𝑏
d) Diagramas.
Se utilizó el software MDSolid para determinar los diagramas de fuerza cortante y momento flexionante.

8. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
Figura 27.1 Plano vertical.

9. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
Figura 27.2 Plano horizontal.

10. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
29 La figura P12-6 ilustra un eje intermedio de una punzonadora que gira a 310 rpm y transmite 20 hp de la
polea para bandas V al engrane. El volante no absorbe ni cede energía en este momento. Considere el peso
de todos los elementos en el análisis.
Figura P12-6. Problema 29
Objetivo Diseñar el eje completo, incluyendo la especificación de la geometría en general y la consideración de
factores de concentración de esfuerzos. El análisis indicaría el diámetro mínimo aceptable en cada punto
del eje, para que sea seguro desde el punto de vista de resistencia.
Datos 𝑃 = 20 𝐻𝑃
𝑛 = 310 𝑟𝑝𝑚
Tablas y/o
gráficas
Apéndice 3. Propiedades de diseño para los aceros al carbón y aleados.
Figura 5-8 Resistencia a la fatiga en función de la resistencia a la tensión, para el acero forjado con varias
condiciones de superficie.
Tabla 5-1 Factores de confiabilidad aproximados.
Figura 5-9 Factor por tamaño.
Fórmulas 𝑆´ 𝑛 = 𝑠 𝑛 𝐶𝑠 𝐶 𝑅
𝑇 =
63000 𝑃
𝑛
𝑊𝑡 = 𝑇/(𝐷/2)
𝑊𝑟 = 𝑊𝑡 𝑡𝑎𝑛Φ
𝐹 𝑁 = 𝐹1 − 𝐹2 = 𝑇/(𝐷/2)
𝐹𝐴 = 1.5𝐹 𝑁
Operaciones
matemáticas,
diagramas y/o
dibujos y/o
representaciones
gráficas y
resultados
Primero se determinan las propiedades del acero para el eje. Del apéndice 3 AISI 1050 acero laminado en
caliente, 𝑠 𝑢 = 90 𝑘𝑠𝑖, 𝑠 𝑦 = 49 𝑘𝑠𝑖 y el porcentaje de elongación es de 15%. Entonces el material tiene
buena ductilidad.
a) Par torsional.
De la figura 5-8 se puede estimar que 𝑠 𝑛 = 26 𝑘𝑠𝑖.
Se debe aplicar un factor por tamaño a la resistencia de fatiga, el diámetro estimado es 𝐷 = 5 𝑖𝑛, entonces
𝐶𝑠 = 0.859 − 0.02125(5) = 0.75275.
También se debe especificar un factor de confiabilidad aproximado de la tabla 5-1. Para este problema, se
diseñará con una confiabilidad de 0.99 y se anejará 𝐶 𝑅 = 0.81. Ya se puede calcular la resistencia a la fatiga
modificada.

11. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
𝑆´ 𝑛 = 𝑠 𝑛 𝐶𝑠 𝐶 𝑅 = (26 000 𝑝𝑠𝑖)(0.75275)(0.81) = 15 852.915 𝑝𝑠𝑖
Se supondrá un factor de diseño de 𝑁 = 2.5 ya que se tiene incertidumbre en las propiedades del material.
Ahora se pasa a calcular el par torsional en el eje, con la ecuación:
𝑇 =
63000 𝑃
𝑛
=
63000 (20 𝐻𝑃)
(310 𝑟𝑝𝑚)
= 4 064.5161 𝑙𝑏 ∙ 𝑝𝑢𝑙𝑔
b) Fuerzas sobre los engranes. Engranes rectos.
La fuerza tangencial se obtiene con la ecuación:
𝑊𝑡 =
𝑇
𝐷
2
=
4 064.5161 𝑙𝑏 ∙ 𝑝𝑢𝑙𝑔
6 𝑝𝑢𝑙𝑔
2
= 1 354.8387 𝑙𝑏 ↓
La fuerza radial se obtiene mediante la ecuación:
𝑊𝑟 = 𝑊𝑡 𝑡𝑎𝑛Φ = (1 354.8387 𝑙𝑏)tan(20°) = 493.1209 𝑙𝑏 →
Fuerza para bandas V.
La fuerza impulsora neta se obtiene mediante la ecuación:
𝐹 𝑁 = 𝐹1 − 𝐹2 =
4 064.5161 𝑙𝑏 ∙ 𝑝𝑢𝑙𝑔
22 𝑝𝑢𝑙𝑔
2
= 369.5014 𝑙𝑏
La fuerza flexionante sobre el eje para transmisiones con bandas V se obtiene:
𝐹𝐴 = 1.5𝐹 𝑁 = 1.5(369.5014 𝑙𝑏) = 554.2522 𝑙𝑏
La fuerza de flexión actúa hacia arriba y hacia la derecha formando un ángulo de 40° con la horizontal.
Como se ve en la figura P12-6, los componentes de la fuerza flexionante son:
𝐹𝐴 𝑥
= 𝐹𝐴 𝐶𝑜𝑠 20° = (554.2522 𝑙𝑏) 𝐶𝑜𝑠 40° = 520.8266 𝑙𝑏 →
𝐹𝐴 𝑦
= 𝐹𝐴 𝑆𝑒𝑛 20° = (554.2522 𝑙𝑏) 𝑆𝑖𝑛 40° = 189.5654 𝑙𝑏 ↑
c) Reacciones es los cojinetes.
Mediante las ecuaciones de estática determinamos las reacciones de los cojinetes.
Plano vertical:
∑ 𝐹𝑦 = 0
𝐹𝐴 − 𝑊𝐴 + 𝑅 𝐵 𝑦
− 𝑊𝐶 + 𝑅 𝐷 𝑦
− 𝑊𝐸 − 𝑊𝑡 = 0
∑ 𝑀 𝐵 = 0
𝐹𝐴(6) − 𝑊𝐴(6) + 𝑅 𝐵 𝑦
(0) + 𝑊𝐶(8) − 𝑅 𝐷 𝑦
(20) + 𝑊𝐸(24) + 𝑊𝑡(24) = 0
Sustituyendo los datos y resolviendo tenemos que las reacciones son:
𝑅 𝐷 𝑦
= −2 320.6760 𝑙𝑏
𝑅 𝐵 𝑦
= 5 200.9493 𝑙𝑏
Plano horizontal:
∑ 𝐹𝑥 = 0
𝐹𝐴 − 𝑅 𝐵 𝑥
− 𝑅 𝐷 𝑥
+ 𝑊𝑟 = 0
∑ 𝑀 𝐵 = 0

12. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
𝐹𝐴(6) + 𝑅 𝐵 𝑥
(0) + 𝑅 𝐷 𝑥
(20) − 𝑊𝑟(24) = 0
Sustituyendo los datos y resolviendo tenemos que las reacciones son:
𝑅 𝐵 𝑥
= 578.4498 𝑙𝑏
𝑅 𝐷 𝑥
= 435.4971 𝑙𝑏
d) Diagramas.
Se utilizó el software MDSolid para determinar los diagramas de fuerza cortante y momento flexionante.
Figura 29.1 Plano vertical

13. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
Figura 29.2 Plano horizontal.

14. Instituto Tecnológico Superior de Guasave
Ingeniería Mecánica
Ing. Rommel Arel Leal Palomares Diseño Mecánico I
Conclusión
El diseño de ejes de transmisión o árboles de transmisión suele ser uno de los procesos más críticos en el diseño
de reductores de velocidad.
En ingeniería mecánica se conoce como eje o árbol de transmisión a todo objeto asimétrico especialmente
diseñado para transmitir potencia. Los ejes sirven para soportar piezas inmóviles, oscilantes o rotatorias de
máquinas, pero no transmiten ningún momento de giro, por lo que generalmente están sometidos a flexión.
Del mismo modo, un árbol de transmisión es un eje que transmite un esfuerzo motor y está sometido a
solicitaciones de torsión. Esto se debe a la transmisión de un par de fuerzas y puede estar sometido a otros tipos
de solicitaciones mecánicas al mismo tiempo.
La configuración típica de un eje es la de un elemento de sección circular escalonado, con mayor sección en el
centro, de manera que los distintos elementos puedan montarse sobre él por los extremos, lo que proporciona
mayor sección resistente en la zona central, donde la flexión ocasiona los mayores esfuerzos.