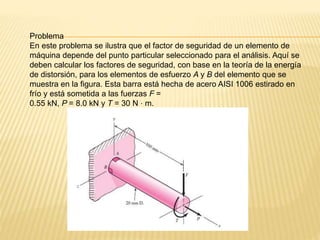
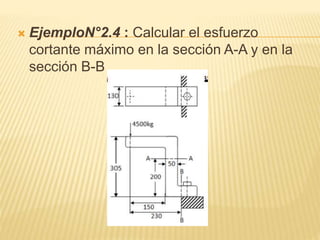
Este documento trata sobre cargas estáticas y fallas. Define una carga estática como una fuerza o par de torsión que no cambia su magnitud, punto de aplicación u orientación. Explica que una falla puede significar que una parte se ha separado, distorsionado permanentemente o comprometido su función. Luego discute varias teorías para predecir fallas como la máxima tensión de corte, energía de distorsión y teorías de Mohr.

1. TORIA DE FALLAS
 Carga Estática

2.  En este capítulo se consideran las relaciones entre la resistencia y la carga estática con
 objeto de tomar decisiones respecto del material y su tratamiento, fabricación y geometría
 para satisfacer los requerimientos de funcionalidad, seguridad, confiabilidad, competitividad,
 facilidad de uso, manufacturabilidad y comerciabilidad.
 CARGA ESTATICA
 Una carga estática es una fuerza estacionaria o un par de torsión que se aplica a un
 elemento. Para ser estacionaria, la fuerza o el par de torsión no deben cambiar su magnitud,
 ni el punto o los puntos de aplicación, ni su dirección. Una carga estática produce tensión o
 compresión axial, una carga cortante, una carga flexionante, una carga torsional o cualquier
 combinación de éstas. Para que se considere estática, la carga no puede cambiar de ninguna
 manera.
 FALLA.
 La falla puede significar que una parte se ha separado en dos o más piezas; se ha
distorsionado permanentemente, arruinando de esta manera su geometría; se ha degradado
su confiabilidad; o se ha comprometido su función, por cualquier razón. Cuando un diseñador
habla de falla puede referirse a cualquiera o todas estas posibilidades.

3. a) Falla de eje estriado de
transmisión de un camión
debida a fatiga por corrosión.
Observe que fue necesario
emplear cinta adhesiva
transparente para sujetar las
piezas. b) Vista directa de la
falla.
Falla por impacto de la masa
de impulsión de la cuchilla de
una podadora de césped. La
cuchilla golpeó un tubo metálico
de marcación de cotas de
topografía.
Figura

4. Falla de un perno de sujeción
de una polea elevada de una
máquina de levantamiento
de pesas. Un error de fabricación
causó una separación
que provocó que el perno
soportara toda la carga de
momento.
Aditamento de ensayo de cadena que falló en un ciclo. Para contrarrestar las quejas de desgaste
excesivo,
el fabricante decidió endurecer el material superficialmente. a) Mitades que presentan la fractura; éste
es un
excelente ejemplo de fractura frágil iniciada por concentración del esfuerzo. b) Vista ampliada de una
parte que
muestra las grietas inducidas por la concentración del esfuerzo en los agujeros del pasador de soporte.

5. CATEGORIAS EN EL DISEÑO DE UN ELEMENTO DE MAQUINA
 1 La falla de la parte pondría en peligro la vida humana, o se
fabrica en cantidades extremadamente grandes; en
consecuencia, se justifica un elaborado programa de ensayos
durante el diseño.
 2 La parte se hace en cantidades lo suficientemente grandes
como para hacer una serie moderada de ensayos.
 3 La parte se hace en cantidades tan pequeñas que los ensayos
no se justifican de ninguna manera, o el diseño se debe
completar tan rápido que no hay tiempo para hacer los ensayos.
 4 La parte ya se ha diseñado, fabricado y ensayado, y se ha
determinado que es insatisfactoria. Se requiere un análisis para
entender por qué la parte es insatisfactoria y lo que se debe
hacer para mejorarla.

6. CONCENTRACION DE TENSIONES
 factor teórico o geométrico de la concentración de esfuerzos Kt o Kts para relacionar el esfuerzo máximo real en
la discontinuidad con el esfuerzo nominal. Los factores se definen por medio de las ecuaciones
Kt =
𝜎max
𝜎𝑜
Kts =
𝜏max
𝜏𝑜
 donde Kt se usa para esfuerzos normales y Kts para esfuerzos cortantes
 Los concentradores de tensión son cualquier discontinuidad en el elemento de maquina, cambio de sección ,
canal chaveteros, agujero, ranura , etc.

7. TEORIAS DE FALLA
Maxima Tension de Corte
Energia de Distorsion
Coulomb Mohr - Ductil
Maxima Tension Normal
Coulomb Mohr – Fragil
Mohr Modificada.

8. Maxima Tension de Corte
La teoría del esfuerzo cortante máximo estipula que la fluencia
comienza cuando el esfuerzo cortante máximo de cualquier
elemento iguala al esfuerzo cortante máximo en una pieza de
ensayo a tensión del mismo material cuando esa pieza comienza a
fluir. La teoría del ECM también se conoce como la teoría de Tresca
o Guest.

9. MAXIMA ENERGIA DE DISTORSION.

12. Teoría de Mohr-Coulomb para materiales dúctiles
No todos los materiales tienen resistencias a la compresión iguales a
sus valores correspondientes en tensión. Por ejemplo, la resistencia
a la fluencia de las aleaciones de magnesio en compresión puede
ser tan pequeña como de 50% de su resistencia a la fluencia en
tensión.

18. MODIFICACIONES DE LA TEORÍA DE MOHR
PARA MATERIALES FRÁGILES

19. Selección de criterios de falla

20. DISEÑO DE EJES: FLEXIÓN Y TORSIÓN
BAJO MUCHAS CONDICIONES LA FUERZA AXIAL F ES CERO O TAN PEQUEÑO QUE SU EFECTO SE
PUEDE IGNORAR , ENTONCES SOLO SE CONSIDERA LA FLEXIÓN Y LA TORSIÓN.
𝜎´
=
16
𝜋𝑑3 (4𝑀2
+ 3𝑇2
)
1
2 𝜏 𝑚𝑎𝑥=
16
𝜋𝑑3 (𝑀2
+ 𝑇2
)
1
2 𝜎´
perm=
𝑆 𝑦
𝑛 𝑑
I =
𝜋𝑑4
64
J =
𝜋𝑑4
32
Según la energía de Distorsion (Von Mises)
d =
16𝑛
𝜋𝑆 𝑦
4𝑀2 + 3𝑇2 1
2
1
3
1
𝑛
=
16𝑛
𝜋𝑑3 𝑆 𝑦
4𝑀2
+ 3𝑇2 1
2
Según el esfuerzo cortante máximo
d =
32𝑛
𝜋𝑆 𝑦
𝑀2 + 𝑇2 1
2
1
3
1
𝑛
=
32𝑛
𝜋𝑑3 𝑆 𝑦
𝑀2
+ 𝑇2 1
2

21. Ejemplo
Considere la llave del ejemplo 5-3, figura 5-16, fabricada con hierro fundido,
maquinada a la dimensión. La fuerza F que se requiere para fracturar esta parte
se puede considerar como la resistencia de la parte componente. Si el material
es una fundición de hierro ASTM grado 30, calcule la fuerza F con:
a) Modelo de falla Mohr-Coulomb.
b) Modelo de falla de Mohr modificado.

24. Problema :
En la figura se muestra una manivela sometida a una fuerza F = 190 lbf la
cual causa torsión y flexión del eje de 34 pulg de diámetro fijado a un soporte
en el origen del sistema de referencia. En realidad, el soporte puede estar en
una situación de inercia que se desea hacer girar, pero para los propósitos de
un análisis de la resistencia se puede considerar que se trata de un problema
de estática. El material del eje AB es acero AISI 1018 laminado en caliente
(tabla A-20). Mediante el empleo de la teoría del esfuerzo cortante máximo,
encuentre el factor de seguridad con base en el esfuerzo en el punto A.

26. Problema
En este problema se ilustra que el factor de seguridad de un elemento de
máquina depende del punto particular seleccionado para el análisis. Aquí se
deben calcular los factores de seguridad, con base en la teoría de la energía
de distorsión, para los elementos de esfuerzo A y B del elemento que se
muestra en la figura. Esta barra está hecha de acero AISI 1006 estirado en
frío y está sometida a las fuerzas F =
0.55 kN, P = 8.0 kN y T = 30 N ⋅ m.

28. Problema
En la figura se muestra un eje montado en cojinetes, en los puntos A y D y
tiene poleas en B y C. Las fuerzas que se muestran actúan en las
superficies de las poleas y representan las tensiones de las bandas. El eje
se hará de una fundición de hierro ASTM grado 25 usando un factor de
diseño nd = 2.8. ¿Qué diámetro se debe usar para el eje? x

31.  EjemploN°2.4 : Calcular el esfuerzo
cortante máximo en la sección A-A y en la
sección B-B

32.  Diagrama del cuerpo libre para la sección A_A

35. EjemploN°2.6 :
El brazo que se muestra en la figura, es parte de un eslabón
en que la fuerza horizontal de 40kg es transferida a F2 que
actúa en forma vertical. La manivela puede pivotar sobre el pin
0.

36.  Solución:
 F2 x 5.5 = 40 x 4
 F2 = 29.09 kg
 La fuerza
descendente F2
provoca un
momento
respecto a la
sección del pin,
existe un momento
de reacción
interna.