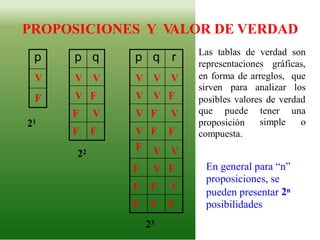
El documento trata sobre las tablas de verdad en lógica proposicional, definiendo sus elementos y cómo se construyen. Explica el valor de verdad de las proposiciones, así como las operaciones lógicas como la conjunción y la disyunción. Además, se presenta un ejercicio para practicar la elaboración de tablas de verdad para diferentes fórmulas lógicas.

1. SISTEMAS INFORMÁTICOS
Matemática para Computadoras
Tema # 2 ….CONTINUACIÓN
TABLAS DE VERDAD
MSc.Ing. María Ivonné Rocha Otondo

2. p
RECORDAR…
Primero recordamos las formulas
que son:
bien formadas
se escribe se lee
P
~P
pΛ q
p
no P
p y q
p o q
si p entonces
p
p
v q
q
q
q
p si y solo si q

3. Valor de verdad de una proposición
El valor de verdad de una
proposición, es la cualidad de
veracidad que describe
adecuadamente la proposición. Esta
puede ser, verdadera (V ó 1) o falsa
(F ó 0)

4. Tabla de verdad
Una tabla de verdad, es la representación
de los posibles valores de verdad que
podría tomar una proposición.
Las tablas de verdad sirven para mostrar
los valores, las relaciones y los resultados
posibles al realizar operaciones lógicas.

5. PROPOSICIONES Y VALOR DE VERDAD
Las tablas de verdad son
representaciones gráficas,
en forma de arreglos, que
sirven para analizar los
posibles valores de verdad
que puede tener
simple
una
o21 proposición
compuesta.
22
En general para “n”
proposiciones, se
2npueden presentar
posibilidades
23
p q r
V V V
V V F
V F V
V F F
F V V
F V F
F F V
F F F
p q
V V
V F
F V
F F
p
V
F

6. Construcción de tablas de verdad
¿Cuántas filas tiene la tabla?



1
2
3
proposición
proposiciones
proposiciones
.........
2 valores (V o F)
4 valores de verdad
8 valores de verdad
 2nn proposiciones valores de verdad.

7. e
a
EJEMPLO:
Vamos a armar nuestra tabla de verdad, primero con
sola proposición, después con dos y tres
una
Si tenemos una proposición y la negamos, tenemos:
p: El perro ladra
~p : no ladra el perro
No olvidemos que la doble negación se convierte
en verdadera o sea: ~ ~p = p
si digo el perro no ladra Su negación será
verdadera:
el perro ladra
si digo el perro ladr
p ~ p
V F
F V
Su negación será falsa:
l perro no ladra

8. ) (p Λ p p V p
V V
F V
F V
F F
(p V p) (
Si tenemos dos proposiciones:
p: el perro ladra
q: el niño llora
podemos unir estas dos proposiciones, mediante la conjunción (v) o la
disyunción(λ), entonces podemos tener:
TAUTOLOGÍA: todo verdad
•
•
(p Λ q): el perro ladra y el niño llora
(p V q): el perro ladra ó el niño llora
p:2 V, 2 F; q:1 V, 1 F intercalado; la Conjunción es V, solo si ambos son V, lo demás
es F; la Disyunción es F si ambos son F lo demás es V, la Condicional es F solo si
el 1º es V y el 2º es F y lo demás es V; la Bicondicional es V si ambos son V ó
ambos son F lo demás es todo F.
p q (p Λ p ) ⇒ p Λ p p V p)
V V V V
V F V F
F V V F
F F V V

9. OTRO EJEMPLO: Trabajamos solo con variables: p, q y r, que
servirán para cualquier tipo de proposiciones.
Evaluar la siguiente fórmula ó esquema molecular:
(p  q)  (p  r)Solución
p q r ( p  q )   ( p   r)
V V V
V V F
V F V
V F F
F V V
F V F
F F V
F F F
V V V
V V V
V F F
V F F
F F V
F F V
F F F
F F F
V
V
V
F
F
F
F
F
V V F F
F V V V
V V F F
F V V V
F F V F
F F V V
F F V F
F F V V

10. EVALUACION de una
FORMULA LOGICA

11. • La característica tabular de una fórmula lógica es
la columna de valores de verdad debajo del
operador de mayor jerarquía. Esta columna puede
presentar los siguientes casos:
1. Cuando todos los valores de verdad son verdaderos,
el esquema es una TAUTOLOGÍA.
2. Cuando todos los valores de verdad son falsos, el
esquema es una CONTRADICCIÓN.
3. Cuando algunos valores de verdad son verdaderos y
otros falsos el esquema es una CONTINGENCIA.

12. PRACTICA
Elaborar las tablas de verdad de las siguientes formulas lógicas
y enviar con su nombre por WhatsAp al celular: 75775151,
junto con las anteriores prácticas
(~P)
⇒
Q
(~P)
⇒
(~Q)
P
⇒
(P v Q)
(P v Q)
⇒
R
(P v Q) ⇒(P
1.
2.
3.
4.
5. V R)