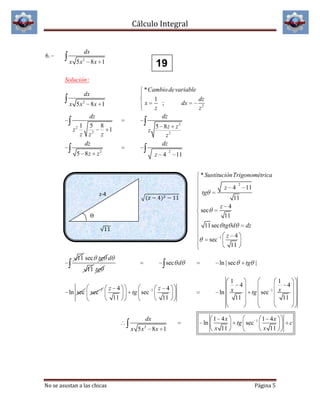
El documento presenta una serie de ejercicios de cálculo integral resueltos. Los ejercicios involucran integrales de funciones racionales, trigonométricas, exponenciales y logarítmicas. Las soluciones utilizan técnicas como sustitución, cambio de variable y propiedades de integrales definidas.

1. Cálculo Integral
EJERCICIOS DE CÁLCULO INTEGRAL
1
1.
3
7x
1
3
dx
4x2
x
Solución :
1
dx
3
1 7 x3
4x2
1
1
x
dz
3
1
1
1
2
1
2
7 1
z
14
1
41
z
1
2
3
4
 
du 
1 1/3 2 z 4dz
2 1 4 z 
z 2  7
4
z
2
1/3
1
4z 7
1
1
ln 2
2
x
4
x
1
2
1
2
4
3
tan
4
7
3
1
ln 4
1
3
1/3
ln 9 12 7
1
ln 4
2
4
1
1
No se asustan a las chicas
3
3
tan
4
3
1/3
1
z
41
z
1
2 z 4 4dz
z2 4z 7
3

tan
tan
a2
1
3
tan
x 3
tan
3
4
3
1
3
1/3
1
4
3
1
1
1 2x
1
1
1
1/3
z 2
ln 1 4 7
4
z 7 1
2
2
z 2
 
 
u2
1/3
dz
2
du

dz
u
1
ln z 2
2
4x 1
dz
4z 7
1/3
1
2
3
1
1
z
2 zdz
2
1
z 4z 7
1/3 2 z
4dz
2
1
z 4z 7
1
x 7x
z2
2
dx
3
1
1
1
tan
4
3
1
3
tan
1
1
3
1
3
1
2
4 2
( )
3 6
Página 1

2. Cálculo Integral
tan xdx
2.
cos 4 x 1
17
Solución :
tan xdx
senxdx
cos 4 x 1
1 2 cos x.
cos x cos 4 x 1
2
cos 2 x
senx .dx
cos 2 x
2
1 1
.
sec
2 cos 2 x
1
tan xdx
cos x 1
2
1
dx
1
2
dx
2
x 1. 2 x
2
1
cos 2 x
c
15
x 1. 2 x
Solución :
2
dx
1
1
dx
2
1
cos 2 x
1
sec
2 cos 2 x
4
3.
1
2
x
3
2
No se asustan a las chicas
3
2
2
3x
1
sin
2
1
dx
2
x2
2 x
1
2
3
2
2
x
1
sin
3
2
2
9
4
2
sin
1
1
1
1
dx
x 1. 2 x
Página 2

3. Cálculo Integral
4.
dx
16
x x5 1
Solución :
Cambio de variable :
x5 1
dx
x x
5
1
x
5
z
x5
dx
x
2
z
1
5 x 4 dx
2 zdz
5
dx
x
1
2 zdz
5 ( z 2 1) z
2 1 2 dz
5 2 z2 1
2 1
tg z
5
2
tg
5
No se asustan a las chicas
1
x5 1
2 zdx
2 zdz
( z 2 1)5
2 dz
5 1 z2
dx
x x
5
1
2
tg
5
1
x5 1
Página 3

4. Cálculo Integral
5.
4
0
sin 2 x.dx
cos 4 x sin 4 x
18
Solución :
1 cos 2 x
2
sin 2 x.dx
4
0 cos 4 x
sin 4 x
cos 2 x
y
4
0
1 cos 2 2 x
2
2
1 2 cos 2 x cos 2 x
4
sin 2 x.dx
4
2 2 cos 2 x
4
1
2
4
0
du

sin 2 x.2.dx
1
2
2
1

a
cot
2
1 cos 2 2 x
2
sin 2 x.dx
4
12
0
cot
1
cot
1
cos 2 x
cos 2 x
cos 2 x
 
 
2
cos
1 2 cos 2 x cos 2 2 x
4
2
2
0
2.
2
sin 2 x.dx
4
0
1 cos 2 x
2
sin 2 x.dx
sin 2 x
2
4
0
u2
2
cot
1
cos 0
4
0
No se asustan a las chicas
0
cot
1
1
sin 2 x.dx
cos 4 x sin 4 x
4
Página 4

5. Cálculo Integral
6.
dx
x 5x2 8x 1
19
Solución :
* Cambio de variable
1
dz
x
;
dx
z
z2
dz
dx
x 5x2 8x 1
dz
1 5 8
z2
1
z z2 z
dz
5 8z z 2
z2
dz
z
5 8z z 2
z 4
2
11
* SustituciónTrigonométrica
tg
z-4
z 4
11
11sec tg d
sec
11 sec tg d
sec d
11
11
sec
ϴ
2
z 4
1
dz
z 4
11
ln | sec
tg |
11 tg
ln sec sec
1
z 4
11
tg sec
1
dx
x 5x
No se asustan a las chicas
2
1
4
ln x
11
z 4
11
ln
8x 1
1 4x
x 11
tg sec
tg sec
1
1
1 4x
x 11
Página 5
1
4
x
11
c

6. Cálculo Integral
7.
x5 1
1
log x3
0
1
x
6
x
2x
6
3
2x
3
x 4 dx
1
20
Solución :
x5 1
1
log x3
0
1
log x3
0
1
1
x
1
2
1
x dx
x5 1
2 x3 1
*u
3
*x 6
4
x5 1
1
x 4 dx
2
0
x5 1
2
x3 1
;
5 x 4 dx
du
1
5
x 4 dx
1
2
0
x5 1
5 x 4 dx
1
x5 1
2
5ln 2
1
22 21
5ln 2
2
5ln 2
0
1
0
22
x5 1
log x3
1
x
6
2x
3
x 4 dx
1
2
5ln 2
dx
a sen x b 2 cos 2 x
8.
2
2
21
Solución :
sec 2 xdx
a 2tg 2 x b 2
dx
2
2
a sen x b 2 cos 2 x
cos 2 x
cos 2 x
dx
a sen x b 2 cos 2 x
2
9.
1
tg
ab
2
2
a.tgx
1
atgx
b
b2
c
dx
e
1
a sec 2 xdx
1
a
x 4 ln 2 x
Solución :
dx
e
x
1
sen
22
1
ln x
1
2
sen
2
sen
1
0
6
1
e
ln x
2
sen
1
ln e
2
sen
1
ln1
2
0
e
1
No se asustan a las chicas
1
dx
x 4 ln 2 x
6
Página 6

7. Cálculo Integral
11.
csc x ctgx
.dx
csc x ctgx
Solución :
csc x ctgx csc x ctgx
csc x ctgx
.dx
csc x ctgx
csc x ctgx
1
2
.dx
csc x ctgx csc x ctgx
.dx
csc x ctgx .dx
csc x ctgx
2
csc 2 x ctg 2 x
csc x.dx
ctgx.dx
2
csc x ctg x
ln csc x ctgx
ln senx
1
cos x
ln senx senx
senx
csc x ctgx
.dx
csc x ctgx
ln
ln
1 cos x
sen 2 x
1 cos x
sen 2 x
24
No se asustan a las chicas
Página 7
.dx

8. Cálculo Integral
6 Integrar
dx
5 x2
du

dx
dx
5 x2
2
5
x2

 u2
a2
sin
7 Integrar
cos x.dx
2 3sin 2 x
1
x
5
C
cos x
dx
2 3sin 2 x
1
3
cos x
dx
2
2
3
sin x
2
3
tan
3 2
1
3 sin x
2
C
dx
8 Integrar
x. 2 x 2 5
du

2.dx
dx
x. 2 x 2 5
2
2x
.
u
2
2x
5
 
u2
a2
5
sec
5
No se asustan a las chicas
1
2x
5
C
Página 8

9. Cálculo Integral
dx
9 Integrar
e2 x 9
du

x
e .dx
dx
e
2x
2
9
2
ex ex
  3

u
a2
u2
1
sec
3
10 Integrar
3x
2
dx
2 x 60
3x
2
1
3
1
ex
3
C
dx
2 x 60
du

dx
2
2
1
179
x
3
   
 3
 
2
u
a2
179
tan
179
11Integrar
1
3x 1
179
C
dx
x 5 x
SOLUCIÓN:
dx
x 5 x
dx
5
2
2
x
5
2
2
2
tan
5
1
2x 5
5
C
cos x.dx
12Integrar
sin x sin 4 x 4
SOLUCIÓN:
No se asustan a las chicas
Página 9

10. Cálculo Integral
cos x
4
dx
sin x sin x 4
du 

2sin x cos x
1
dx
2 sin 2 x sin 2 x 2 22
   
  a2
û
u2
1
sec
4
1
sin 2 x
2
c
Analizamos sin 4 x 4 :
sin 4 x 4 0
sin 4 x
4
4
sin x, no puede ser mayor que 4; porque el rango sin 4 x
cos x
sin x sin 4 x 4
13Integrar
0;1
dx
2 x 7 .dx
x2 2x 5
SOLUCIÓN:
2 x 7 .dx
x2 2x 5
du 

2 x 2 .dx
5
x 22 x 
  5
u
du

dx
2
x 1
22
 
a2
u2
ln x 2 2 x 5
No se asustan a las chicas
5
tan
2
1
x 1
2
C
Página 10

11. Cálculo Integral
18 Integrar
sin 2 x.dx
sin 4 x cos 4 x
SOLUCIÓN:
4
sin 2 x.dx
sin 4 x cos 4 x
0
4
0
4
0
sin 2 x.dx
1 cos 2 x
2
du
 

sin 2 x.2.dx
2
1 cos 2 x
2
2
2
cos 2 x
12
  
  a2
u2
tan
cos 2 x
4
0
tan
No se asustan a las chicas
1
1
0
1
tan
1
o
4
4
Página 11

12. Cálculo Integral
4
23 Integrar
tan x.dx
cos 2 x
0
SOLUCIÓN:
tan x.dx
cos 2 x
4
sin x.dx
4
4
0
cos x 2 cos 2 x 1
sin x.dx
0
0
1
2
cos x 2 cos 2 x
1
2
sin x.dx
4
0
cos x
cos x
1
2
2
2
4
1 1
.
.sec
2 1
2
sec
1
sec
1
1
2 cos
2.
1
2
4
cos x
1
2
0
sec
sec
1
1
2 cos 0
2.0
sec
No se asustan a las chicas
1
1
sec
1
0
Página 12