Tello buque 1

PROBLEMAS RESUELTOS DE TEORIA DE BUQUE I
1- Mencione los efectos que produce en un buque la variación de su eslora.
La variación de la eslora de un buque puede ocasionar que se presente Hogging o Sagging
(Tensión o comprensión) y con ello el buque tiene menos estabilidad, y puede producirse la
ruptura del casco.
2- Que es limitación del calado y cuando se da explique brevemente.
El límite del calado lo dá el disco de plimsoll, lo cual menciona que, al llegar el agua hasta esa
marca, esa sería el límite de carga que puede llevar el buque sin tener percances en la
navegación.
3- Tres ordenadas consecutivas en el plano de agua de un barco, separadas 4 metros,
son 12, 13 y 13,5 m, respectivamente. Encuentra el área entre las dos últimas
ordenadas.
Usando Regla (5-8):
( )
( )
2
5
8
5 8
12
:
4
5 13,5 8(13) 12
12
53,16
s
A p m i
Entonces
A
A m
= + −
= + −
=
 
 
4
4
12 13 13,5

4- Un flotador de 60 x 12 (ver figura planos de flotación constante). Determinar el área del
plano de flotación (utilizar Simpson mínimo 3 ordenadas)
Solución:
:
( )
( ) ( )
( ) ( )
2
2
2
1
2
2 2
1 2
: 1. 4. 1.
3
11 10
1.6 4.6 1.6 1.6 4.3 1.0 192
3 3
21 9
1.6 4.(4,5) 1.3 1.6 4.6 1.6 297
3 3
1 9
92 29 8
7 4
WL
s
Usamos la primera regla de simpson A a b c
A m
A m
A A m
A m m
= + +
= + + + + + =
= + + + + + =
→ = + = + =

5- Un flotador de 60 x 12 x 6 (ver figura sección transversal a proa y popa comenzando
de derecha a izquierda). Determinar el Desplazamiento al calado de 4.5 m (utilizar para
el cálculo del volumen método de integración aproximada por regla de Simpson utilizar
5 ordenadas).
Solución:
( )
,
:
: 1. 4. 1.
3
Dado que nos pide el calculo del volumen por simpson
debemos de hallar las áreas y las areas las podemos
hallar con cualquier método
s
Usamos la primera regla de simpson A a b c
= + +
8

( )
2
1
2
2
2
3
2
4
2
5
1 2 3 4 5
4,5 :
13,5 12 13,5 39
12 10,5 12 34,5
10,5 9 10,5 30
9 7,5 9 25,5
7,5 6 7,5 21
:
1. 4. 2. 4. 1.
3
Las áreas con respecto al calado son
A m
A m
A m
A m
A m
Usamos la primera regla de simpson para volumenes
s
A A A A A
= + + =
= + + =
= + + =
= + + =
= + + =
∇= + + + +
∇ = ( )
3
3
3
15
1.39 4.(34,5) 2.30 4.(25,5) 1.21
3
1800 ; 1,025
.1,025 1800.(1,025
1
) 1485
845
sw
n
ton
m
o
m
ton
m
t
+ + + +
∇
= ρ
=
=
∇ =
=
=



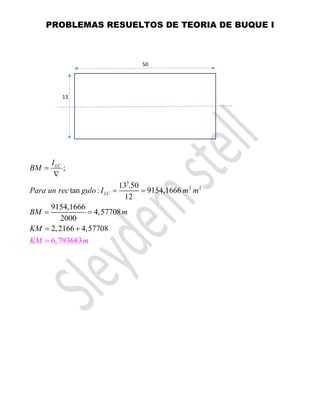
6- Un flotador de 50 x 15 x 6 tiene sección
transversal constante como muestra la figura,
al calado 4 de m determinar altura del
metacentro desde línea base (utilizar para
momentos regla de Simpson).
Solución:
Altura del Metacentro (KM)
( )
( )
( )
[ ]
2
1 3
1 3
1 1 2 3 3
2 2
2
1. . 4. . 1. .
3 2
( )
1 1
1.0.400 4. 1 .400 1.2.400 1.2.550 4.3.600 1.4.650
3 3
2000
4433.333
2,2166
2000
T T
T T
T A A T A
M yz
KB
KB
KB m
+
 
   + 
 
  + +
 
 
 
 
= =
∇ ∇
+ + + + +
 
 
=
= =

3
2 2
;
13 .50
tan : 9154,1666
12
9154,1666
4,57708
2000
2,2166 4,57708
6,793683
LC
LC
I
B
m
M
Para un rec gulo I m m
BM m
M
KM
K
=
∇
= =
= =
=
=
+
50
13

7- El hidroavión de una embarcación tiene las siguientes semiordenadas espaciadas a
15m de distancia comenzando en el perpendicular:
0,50 6,00 12,00 16,00 15,00 9,00 y 0 metros.
Calcule el momento de inercia sobre LCF.
Solución:
LCF (Centro de Flotación)
2 2 2 2 2 2 2
1 1 2 2 3 3 4 4 5 5 6 6 7 7
2 2 2 2 2 2 2
1. . 4. . 2. . 4. . 2. . 4. . 1. . .2
3
2, .
15
1.0,5.0 4.6.15 2.12.30 4.16.45 2.15.60 4.9.75 1.0.90 .2
3
y
y
y
s
I y x y x y x y x y x y x y x
Se está multiplicando por porque se está tomando media manga
I
I
 
= + + + + + +
 
 
= + + + + + +
 
2 2
4671000m m
=

[ ]
[ ]
1 1 2 2 3 3 4 4 5 5 6 6 7 7
1 2 3 4 5 6 7
1. . 4. . 2. . 4. . 2. . 4. . 1. .
3 .2
2, .
1. 4. 2. 4. 2. 4. 1. .2
3
2,
wp
wp
s
y x y x y x y x y x y x y x
x
A
s
A y y y y y y y
Se está multiplicando por porque se está toma
+ + + + + +
=
= + + + + + +
[ ]
[ ]
2 2
2
2
.
15
1.0,5 4.6 2.12 4.16 2.15 4.9 1.0 .2
3
1785
15
1.0,5.0 4.6.15 2.12.30 4.16.45 2.15.60 4.9.75 1.0.0
3 .2
1785
47,394987
4671000 1
3
785(47, 7
661 8 9
39495
6,
)
wp
wp
CF
CF
ndo media manga
A
A
I
m
x
x
m
m
m
I
= + + + + + +
=
+ + + + + +
=
=
= −
=

8- Un flotador de 30 x 10 al calado de 3 m tiene el plano de flotación como muestra la
figura. Calcule centro de flotación longitudinal.
Solución:
[ ] [ ] [ ]
1,5 11 2,5
1.0.25 4.5.(23,5) 1.10.22 1.10.2
.
2 4.8.11 0 0 4.3.(2,5) 0
3 3 3
206
2417,3333
11,7346
20
1,7346 s c
6
e
wp
xy
y
o
A
y
y
LCF a p pa de la ción medi
m
a
=
+ + + + + − + +
=
=
=
=
∫

9- Un buque DD-348 se encuentra al calado de 9’ (KG = 15.5´). A bordo del buque se
efectúa un movimiento de un peso de 25 ton en un compartimiento cuyo centro de
gravedad está a 5’ sobre la quilla, llevándolo a una posición situada a 20’ de altura
respecto de esta. Cuál es la condición de equilibrio en que se encuentra el buque por
este movimiento de peso.
Solución:
1
De las graficas de curvas hidrostaticas a un calado de 9',
tenemos que su =1450ton y KM=17,125' ; KG=15,5'
.
' ; 20' 5' 15'
25.15
' 0.258602'
1450
' ' 15,758
17,125 7
62'
5, 5 62
'
1 8
w d
GG d
GG
KG KG GG
GM KM KG
GM
= = − =
= =
= + =
=
= −
= −



△
△
,3663'( )
equilibrio estable
25
25
5’
20’

10-En un dibujo represente la eslora L según el convenio de Arqueo de 1969. Indique con
simbologías apropiadas en representación.
Solución:
(1). Trazamos una linea de flotación a 0,85D
(2). Trazamos la perpendicular de popa que pasa por la
interseccion de (1) y la roda.
(3)Trazamos la per
96
pend
%
si L=a L=a
icular de proa.
si
L LWL
=
→
∴
L=b L=Lpp
→
11- A qué razones (mencionar 3) puede atribuirse una disminución de la altura
metacéntrica en un buque.
Solución:
1. Aumentar pesos en la cubierta de la embarcación.
2. Subir pesos de la parte más baja de la embarcación hacia la cubierta.
3. Quitar pesos de la parte más baja de la embarcación.

12-El desplazamiento de un barco es de 4500 toneladas y KG = 5 m. Se carga la siguiente
carga: 450 toneladas kg = 7,5 m, 120 toneladas kg = 6,0 m, 650 toneladas kg = 3,0 m.
Encuentre la cantidad de carga a cargar en una cubierta intermedia (Kg = 6 m) de
modo que el barco navegue con un GM = 0.6 m. (La carga KM es de 5,6 m.)
Solución:
1 1 2 2 3 3 4 4
4500 ; 5 ; ' 5,6 ;
0,6 ; 5,6
450 ; 7,5
120 ; 6,0
650 ; 3,0
; 6,0
'
. . . . .
'
4500.5 450.7,5 1
'
ton KG m KM m
GM m KM m
ton Kg m
ton Kg m
Adicionan
ton Kg m
xton Kg m
GM KM KG
KG w Kg w Kg w Kg w Kg
KG
Desplazamiento final
KG
= =
= =
=

 =


=

 =

= −
+ + + +
=
+ +
=
Datos :
△=
△
s
2
n
0.6 650.3 .6
4500 450 120 650
28545 6.
'
5720
Re : '
28545 6.
0,6 5,6 55
5720
La ca tidad de carga es 55 tonelada
x
x
x
KG
x
emplazando los valores en GM KM KG
x
x
x
∴
+ +
+ + + +
+
=
+
= −
+
= − → =
+

13-Un flotador de 50 x 10 (ver figura planos de flotación constante) se encuentra flotando
al calado de 3 m. Se embarcan: 50 ton de lastre en tanques de doble fondo Kg = 0.8 m,
200 ton en Kg = 3.5 m, así mismo se mueven 80 ton desde Kg = 2.5 m hasta Kg = 6 m.
Calcule Altura metacéntrica.
Solución:
2 3
1 1 2 2
: 3 ; 3,8
400 400.3 1200 .1,025 1230
:
50 0,8
200 3,5
var :
. . .
'
1230.3,8 50.0,8 200.3
'
wp
Datos iniciales T m KG m
A m m ton
Se adicionan
ton Kg m
ton Kg m
Debido a la adicion ia el KG
KG w Kg w Kg
KG
KG
= =
= →
= = →
= =
→ =
→ =
+ +
=
+ +
=
▽ △ ▽
△
3
,5
3,658
1230 50 200
var ( ) :
( ') :
'
.
250
' 3
400.1,025
' 3,6097 1443,88 1480
wp
volumen final desplazamiento fina
m
Debido a la adicion de pesos ia el calado T
Calado final T
peso adicionado
T calado inicial
A
T
T m m ton
=
+ +
+
= +
= →
= →
=



ρ
▽' △'
l





80
Debido a este movimiento varia el KG':
KG''=KG'+GG'
peso movido.variacion del KG verticalmente
GG'=
variacion del KG verticalmente 6 2,5 3,5
80.3,5
GG'= 0,1891 KG''=3,8471
1480
Hallando la
Se mueve toneladas
m
m m
=− =
= →
△'
3 3 3
1 2 3
3 3 3
altura metacentrica (GM):
'
- '', ; 1,80485
2
1
; . 1. 4. 1. .2
3 3
2, .
1 5
. 1.0 4.(2,5) 1.5
3 3
LC
LC
LC
T
GM KM KG KM KB BM KB m
I s
BM I y y y
I
= =
+ =
=
 
 
= = + +
 
 
 
 
 
= + +
  
 
▽'
3 3 3 3 3 3
2 2
1 15 1 5
. 1.5 4.5 1.5 . 1.5 4.(2,5) 1.0
3 3 3 3
2916,666
2916,666
2
2,020
1443,88
1,80485 2,02 3
0,0 225
0 ,8471
LC
GM m
I m m BM m
GM
 
   
   
+ + + + + +
    
 
   
   
 
= →
=
= −
=
= + −

14-Un buque DD-348 se encuentra al calado de 9’3” (KG = 14’). Se embarcan 60 ton en
Kg = 14’, 80 ton en Kg = 8’ y se desembarcan 140 ton de Kg = 5’. Determinar el área
bajo la curva de brazos adrizantes hasta 40°.
Solución:
  
 
lg
1 1 2 2 3 3
1' 12'' 9,25'
: 1500 ; 1500
Debido al embarco y desembarco hay una variacon del KG
. . . .
'
pie pu ada inicial
ft in
inicial final
T
Por curvas hidrostaticas tenemos ton ton
KG w Kg w Kg w Kg
KG
K
= → =
= =
+ + −
=
Δ Δ
△
40
40
1500.14 60.14 80.8 14.5
' 14,52' ( ': )
1500
Por curvas cruzadas tenemos: GZ 2,75' 12'
: ' ; '
12 14,52 2,52'
GZ' 2,75 2,52. (40 ) 1,1301'
Para hallar
G KG KG final
con un Kg
Correccion del GZ GZ GZ GGsen GG Kg KG
GG
sen
θ
+ + −
=
= =
=
+ =
−
=
− =
−
= − °
=
el Area bajo la curva de brazos adrizantes hasta 40°,
debemos de encontrar los GZ; por curcas cruzadas de 30°, 20°, 10°, 0° y luego calcular
la corrección.
Angulo GZ '
0 0 0
10 0,85 0,4124
20 1,65 0,7881
30 2,35 1,
GZ
( )
( )
1 2 3 4 5
09
40 2,75 1,1301
:
1. 4. 2. 4. 1.
3
10
1.0 4.(0,4124) 2.(0,7881) 4.(1,09) 1.(1,1301)
3
0,5070 .
57,3
Cálculamos Area por Si
m
mpson
s
A y y y y y
rad
A
A rad
=
= + + + +
°  
= + + + +
 
°
 

15-Un flotador de 35 x 16 (figura planos de flotación constante) se encuentra al calado de
2.5 m. (KG = 2.5 m). Embarque un peso de 2 ton en Kg = 3 m y a 2 m a estribor de
crujía tal que este no produzca trimado en esas condiciones Calcular la escora que
produce este embarco.
Solución:


 
 

2
3
:
2,5
360
900
922,5 ; KG 2,5
.
angulos de escora está dada por: tan( )
. '
:
924,5
'
inicial
wp
inicial
inicial inicial
final inicial
inicial
Datos iniciales
T m
A m
m
ton m
w d
El
GM
En el embarco ocurre
peso embarco ton
KG
θ
=
=
=
=
=
=
+ =
=
∇
Δ
Δ
Δ Δ
Δ 
. .
922,5.2,5 2.3
' 2,501
924,5
inicial
KG peso embarco Kg
KG m
+
+
=
8
12,5
5
16 5 12,5



3 3 3
1 2 3
Hallando la altura metacentrica (GM'):
' - '
'
2
'
.
2
' 2,5 2,50542 1,2527
360.1,025
1
; . 1. 4. 1. .2
3 3
wp
final
LC
LC
final
GM KM KG
KM KB BM
T
KB
peso embarco
T calado inicial
A
T m KB m
I s
BM I y y y
Se está multip
=
= +
=
+
= +
= →
=
 
 
= = + +
 
 
 
ρ
∇
3 3 3 3 3 3
2 2
2, .
1 5 1 12,5
. 1.8 4.(8) 1.8 . 1.4 4.4 1.4 .2
3 3 3 3
4480
4480 4,9670
360.2,50542
' 1,25271 4,9670 2,501 3,7187
2.2
tan( )
9
LC
LC
licando por porque se está tomando media manga
I
I m m BM m
GM m
θ
 
   
   
= + + + + +
   
 
   
   
 
= →= =
= + − =
= 0,0011634
24,5.3,7187
arctan(0,001163
6
4)
0,066 5
θ
θ
= °
=
=

16-Un barco de 10000 toneladas de desplazamiento tiene KG=5,5m; KB=2,8m y BM=3m.
Calcule los momentos de estabilidad estática en
(a) Escora de 5 grados
(b) Escora de 25 grados
Solución:

:
10000 ; KG 5,5 ; 2,8 ; 3
.
( ) Para el ángulo de 5° usamos: GZ=GM.sen( )
-
2,8 3 5,5 0,3 0,0261
( ) Para el ángulo de 2
10000.0,0261
261 .
final
Mt
datos iniciales
ton m KB m BM m
Mto GZ
a
GM KM KG
KM KB BM
GM m GZ m
b
o
Mto ton m
θ
= = = =
=
=
= +
= −
=
= → =
=
+
Δ
Δ
2
2
5° dado que no tenemos curvas
cruzadas usamos:
1
GZ= .tan
2
1
GZ= 0,3 3.tan (25 ) (2
,
10000
5 )
2
0 2646
.0,2646
2646 .
Mto
Mto ton m
GM BM sen
sen
GZ m
θ θ
 
+
 
 
 
+ ° °
 
 
=
=
=

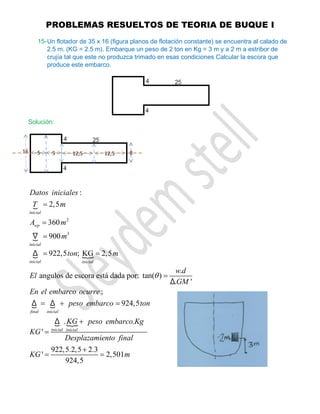
17-Un buque tiene LBP = 60 m se encuentra al calado de 4.5 m. Calcular su
desplazamiento asuma que el área en la estación 3 es de 12.8 m2
Solución:
1
2
2
2
1
2
2
2
2
Por curva de Bonjeans tenemos:
2 43,75
2 50
1 50
1 50
1 32,5
2
0 0 ( )
:
10
1.12,8 4.43,75 2.50 4.50 2.50 4.32,5
3
A de m
A de m
A de m son iguales por cuerpos paralelos
A de m
A de m
A de Por la grafica
Volumen por simpson
=

=


= 

= 

=
=
= + + + + +
∇ [ ]
3
3
2
1.0
2392,666
( ) 1,025
.
2392,666.1,025
452,483ton
m
ton
Densidad agua salada
m
ρ
ρ
+
=
=
=
=
=
∇
△ ∇
△
△

18-Una embarcación en forma de caja (65m 12m 8m) tiene un KG 4m, se encuentra
flotando en agua salada con un calado de 4m en proa y popa, determinar el momento
de estabilidad Estática a 5 grados y a 25 grados.
Solución:

3
3
3
Para 5 grados:
65.12.4 3120 .1,025 3198
4 ; 4
:
. ; ( );
; ; ;
2
.
( que la embarcacion tiene forma de caja)
12
12 .65
KB=2m; BM=
12.312
LC
final
LC
m ton
T m KG m
sabemos
Mto GZ GZ GMsen GM KM KG
I
T
KM KB BM KB BM
B L
I Dado
θ
= = →
= =
= =
= = = −
=
+ = =
=
⇒
▽ △ ▽
△
∇
2
3 5
0
1 0,0871
Para 25 grados:
Como en este caso no tenemos
3198.0,0871 278,5458 .
c
curvas cruzadas usamos la
e uación aproximada de estabilidad a grandes angulos.
1
GZ= .tan
2
m KM m
GM m G
M
M n
Z m
G
to to m
M B θ
= → =
→ = → =
 
+

 
∴
= =
2
1
GZ= 1 .3.tan (25 ) (2
1
5 )
2
0,5
3198.0,5604
792,355 .
4
60
Mto
Mto ton m
sen
sen
GZ m
θ

 
+ ° °
 
 
=
=
=

19-Un flotador paralelepipédico de 70x10 flota con un calado de 3m (KG=4,1m), se
embarca lastre en 2 tanques de doble fondo de 10x5x1. Determine:
a) Momento de adrizamiento a 20°
b) El área bajo la curva de estabilidad estática hasta 40°
Solución:

2
a):
2152,5
.
70.10.3 2(10.5.1) 1,025 2255
Como el angulo es mayor a 10° y no tenemos curvas cruzadas,
entonces usamos:
1
GZ= .tan ...............(1)
2
final
ton
Mto GZ
ton
GM BM sen
θ θ
=
=
 
 
= + =
 
 
 
 
+
 
 




∇
△
△'
△'


3
3
'
'
; ; ;
2
.
( que la embarcacion es paralelepipedica)
12
10 .70
BM= 2,6515
12.2200
'
.
2.50
' 3 3,1428 1,5714
70.10.1,025
LC
final
LC
wp
final
GM KM KG
I
T
KM KB BM KB BM
B L
I Dado
m
peso adicionado
T calado inicial
A
T m KB m
KM
= −
=
+ = =
=
=
+
= +
= →
=
→
∇
ρ
1 1
1,5714 2,6515 4,2229
var :
. .
'
2100.4,1 2.50.0,5
' 3,9363
2100 100
m
Debido al embarco el KG ia
KG w Kg
KG
KG m
= + =
+
=
+
=
+
△

2
20
4,2229 3,9363 0,2866
(1) :
1
GZ = 0,2866 .2,6515.tan (20 ) (20 ) 0,1580
2
b):
Por cálculos anteriores tenemos:
2255 ; BM=2,6515 ; 4,2229 ;
' 3,9363
2
2 55.0,1580 356,29
356,29 .
GM m
en
sen m
ton m K
m
M m
KG
Mto
Mto ton
°
= =
→ = − =
 
+ ° ° =

=
=

 
=
=
△'
0 10 20 30 40
; 0,2866
para 0< 10° usamos GZ=GM ( ) y para 10
(1) :
GZ GZ GZ GZ GZ
0 0,051 0,158 0,367 0,788
:
10 1
1.0 4(0,051) 2(0,158) 4(0,36
3 57,3
m GM m
sen
usamos la ecuación
Área por simpson
rad
A
θ θ θ
° ° ° °
=
≤ > °
°  
= + + +
 
°
 
[ ]
1
7) 1(0,788)
0,16 4 .
A rad m
+
=

Tello buque 1

Más contenido relacionado

La actualidad más candente

Similar a Tello buque 1

Más de JAVIERTELLOCAMPOS

Último

Tello buque 1