1) El documento trata sobre sistemas de composición variable y equilibrio de fases. 2) Explica conceptos como sistema, propiedades, fase, equilibrio y presenta la relación fundamental entre las propiedades termodinámicas para mezclas homogéneas de composición variable. 3) El objetivo es determinar las propiedades termodinámicas para mezclas y resolver problemas de sistemas en equilibrio líquido/vapor considerando un comportamiento ideal.

1. CAPITULO III
SISTEMAS DE
COMPORTAMIENTO IDEAL Y
EQUILIBRIO DE FASES

2. 74
CAPITULO III
SISTEMA DE COMPORTAMIENTO IDEAL Y EQUILIBRIO DE FASES
En el tema anterior se trataron las propiedades termodinámicas de
fluidos de composición constante; sin embargo en los procesos industriales
los sistemas están formados por mezclas multicomponentes, de gases o
líquidos donde la composición varía debido a los diferentes procesos de
mezclado o separación, transferencia de componentes de una fase a otra o
reacciones químicas. Por tanto, las propiedades termodinámicas de esos
sistemas no sólo dependen de la temperatura y presión sino también de la
composición. Por consiguiente la primera tarea de este tema es desarrollar
una relación fundamental entre las propiedades para mezclas fluidas
homogéneas de composición variable y se estudiará el equilibrio de sistemas
binarios y multicomponentes vapor-líquido bajo condiciones ideales.

3. 75
OBJETIVOS
OBJETIVO TERMINAL:
Al finalizar el tema, el estudiante estará en capacidad de determinar
las propiedades termodinámicas para mezclas de composición variable y
podrá resolver problemas de sistemas en equilibrio líquido/vapor,
considerando comportamiento ideal.
OBJETIVOS ESPECÍFICOS:
3 Desarrollar el criterio de equilibrio de fases a partir de la relación
fundamental para mezclas homogéneas de composición variable.
3 Determinar las propiedades termodinámicas para mezclas de gases
ideales y soluciones líquidas ideales.
3 Calcular el punto de rocío y punto de burbuja y realizar el cálculo de
vaporización instantánea para mezclas ideales.

4. 113
TEMA Nº 2
SISTEMA DE COMPOSICIÓN VARIABLE COMPORTAMIENTO IDEAL
2.1. CONCEPTOS BÁSICOS DE EQUILIBRIO DE FASE:
En el estudio de gases, es necesario y conveniente tener presente una
serie de definiciones de términos y conceptos. Las siguientes son las
principales:
Sistema: Cuerpo de materia con límites finitos (definidos) que puede
considerarse, si se desea, aislado del medio que lo rodea. Representa el
material bajo consideración para un proceso dado. Ejemplo: hidrocarburos
en un yacimiento.
Propiedades: Características de un sistema que pueden evaluarse
cuantitativamente como resultado de un experimento. Describen la condición
a un tiempo particular. Se miden en función de fuerza (f), longitud (L),
Tiempo (t), o temperatura (T). Existen dos tipos de propiedades.
a) Propiedades Extensivas: Dependen de la cantidad de materia, es decir,
extensión del sistema. Ejemplos: volumen, masa.
b) Propiedades Intensivas: Son independientes de la extensión o cantidad
de materia del sistema. Ejemplos: temperatura, presión, densidad.
Sistema homogéneo: Sistema cuyas propiedades intensivas varían
continua y uniformemente de punto a punto en el sistema entre planos

5. 114
perpendiculares a la fuerza de gravedad. Ejemplos: un balón que contiene
helio; un yacimiento por encima de su punto de saturación (burbujeo).
Sistema heterogéneo: Sistema compuesto por dos o más sistemas
homogéneos y cuyas propiedades intensivas cambian bruscamente en las
superficies de contacto. Ejemplos: un yacimiento por debajo de la presión
de saturación, petróleo más agua.
Fase: Cuerpo de material homogéneo diferente en sus propiedades a
los demás que lo rodean. Las regiones (sistemas) homogéneos, discutidas
en sistemas heterogéneos, se refieren a fases. Existen sólo una fase
gaseosa, pero varias fases de líquido y de sólidos.
Interfase: Se refiere a la superficie de contacto entre dos fases.
Fluido: Se refiere a gas, líquido o mezcla de éstos.
Componente: Como en este tema no se considera reacciones
químicas, bajo estas circunstancias un componente se define como una
sustancia que comprende un solo tipo de moléculas. Ejemplos: dióxido de
carbono, agua destilada, propano, petróleo crudo es una mezcla de
componentes.
Nota: En análisis de mezclas de hidrocarburos, gases y líquidos,
debido a la dificultad de analizar todos los componentes, se agrupa bajo el
nombre de un solo componente del sistema, cierta parte del mismo, tal por

6. 115
ejemplo: C+7 heptanos y compuestos mas pesados, el cual para propósitos
de cálculos, se trata como un solo componente. De allí que componente se
defina en otras formas:
a) Elemento constitutivo de un sistema cuya concentración puede sufrir
variación independiente en las diferentes fases.
b) Elemento constitutivo que toma parte en el equilibrio de un sistema.
c) Cualquiera del menor número de elementos constitutivos independientes
por la cual pueda expresarse la composición de cada una de las fases de
un sistema.
Número de Componentes: Es el número total de elementos
constitutivos químicos diferentes en un sistema, menos el número de
reacciones químicas distintas que pueden ocurrir entre estos elementos
constitutivos del sistema.
Número de Grados de Libertad (Variación): También se denomina
regla de fases de Gibbs. Es el número de variables (grados de libertad)
requeridas para determinar el estado de un sistema en equilibrio. Se
expresa generalmente por la ecuación:
F = C – P + 2
Donde: C = número de componentes constitutivos del sistema.
P = número de fases.
F = número de grados de libertad o número de variables requeridas
para determinar el estado de un sistema en equilibrio.

7. 116
Estado: Condición de un sistema a un tiempo particular. Se
determina cuando todas las propiedades intensivas del sistema son fijas.
El número mínimo de propiedades que deben describirse para fijar las
propiedades dependen del número de componentes y fases presentes en el
sistema.
Equilibrio: Se considera que existe equilibrio en un sistema, cuando
sus propiedades intensivas permanecen constantes con el tiempo, bajo las
condiciones a que existe el sistema.
Presión de Vapor: Es la presión que ejerce la fase de vapor en el
recipiente que lo contiene, cuando líquido y vapor de un componente puro se
encuentran en equilibrio a determinadas condición de presión y temperatura.
El número de moléculas que se escapan del líquido, es igual al número de
moléculas que regresan a el.
Punto de Rocío: Estado de un sistema completamente gaseoso en
equilibrio con una cantidad infinitesimal de líquido.
Presión y Temperatura de Rocío: Presión y temperatura de un
sistema en el estado de punto de rocío.
Punto de Burbujeo: Estado de un sistema completamente líquido en
equilibrio con una cantidad infinitesimal de gas.

8. 117
Presión y Temperatura de Burbujeo: Presión y temperatura de un
sistema en el estado de punto de burbujeo.
Gas o Vapor Saturado: Vapor (gas) en equilibrio con un líquido, a
una presión y temperatura dadas. En el caso de sustancias puras, es el
estado de gas o vapor correspondientes al punto de rocío.
Líquido Saturado: Líquido en equilibrio con vapor (gas) a una
presión y temperatura dadas. En el caso de sustancias puras, es el estado
de líquido correspondientes al punto de burbujeo.
Curva de Punto de Rocío: Lugar geométrico de los puntos de
presión y temperatura al cual se forma la primera gota de líquido, al pasar un
sistema del estado (región) de vapor (gas), al estado (región) de dos fases.
Comúnmente se denomina Curva de Rocío.
Curva del Punto de Equilibrio: Lugar geométrico de los puntos de
presión y temperatura al cual se forma la primera burbuja, al pasar un
sistema del estado (región) líquido, al estado de (región) de dos fases.
Comúnmente se denomina Curva de Burbujeo.
Región de dos fases: Región (zona) encerrada por las curvas de
punto de rocío y de burbujeo, en un diagrama presión temperatura del
sistema, donde el gas y líquido coexisten en equilibrio.
Constante de Equilibrio (Valores –K) de un Componente: Es la
razón de la fracción molar del componente en fase gaseosa y en la fase
líquida, en un sistema en equilibrio, K = y/x.

9. 118
Punto de Ebullición Normal: Temperatura que produce en un
componente puro, una presión de vapor igual a una atmósfera.
Condiciones críticas: Condiciones a la cual las propiedades
intensivas de las fases líquido y vapor coexistentes, llegan a ser idénticas.
2.2. RELACIÓN FUNDAMENTAL ENTRE PROPIEDADES
TERMODINAMICAS PARA MEZCLAS HOMOGENEAS DE
COMPOSICIÓN VARIABLE:
La ecuación (2.1) relaciona la Energía Libre de Gibbs con la P y T de
cualquier sistema cerrado.
( ) ( ) ( )dT
nS
dP
nV
nG
d −
= (2.1)
Esta ecuación se aplica al caso de:
Sistema 1 sola fase.
Composición constante (No sufre reacción química)
Cerrado
Tenemos:
[∂ (nG)/∂P]T,n = (nV) y
[∂ (nG)/∂T]P,n = - nS
donde n indica que el número de moles de todos los componentes químicos
se mantienen constantes.

10. 119
Para sistemas abiertos
1 sola fase.
Composición variable (Intercambios de masa con
los alrededores.
En este caso la energía libre de Gibbs no sólo es función de la P y T
sino también del número de moles (se toma o se agrega material al
sistema).
Entonces:
nG = g (P, T, n1, n2, ... , ni)
Donde ni: corresponde al número de moles de los componentes.
La diferencia total de (nG) es:
( ) ( )
[ ] ( )
[ ] ( )
[ ] i
n
,
T
,
P
i
n
,
P
n
,
T dn
n
nG
dT
T
nG
dP
P
nG
nG
d j
⋅
∂
∂
+
∂
∂
+
∂
∂
= ∑
Donde: la sumatoria ∑, se aplica a todos los componentes presentes.
nj: indica que se mantienen constantes todos los números de moles,
diferentes de ni.
Luego: Reemplazando las dos primeras derivadas por (nV) y (nS).
( ) ( ) ( ) ( )
[ ] i
nj
,
T
,
P
i dn
n
nG
dT
nS
dP
nV
nG
d ⋅
∂
∂
+
−
= ∑
(2.2)
2.3. POTENCIAL QUÍMICO DEL COMPONENTE I EN UNA MEZCLA (μi):
Se define como la variación de cualquier propiedad del sistema
con respecto al número de moles de un componente i en particular,

11. 120
manteniendo la P, T y el resto de los componentes diferentes al componente
en particular (i) constantes.
( )
[ ] j
n
,
T
,
P
i
i n
nM ∂
∂
=
μ
M: representa cualquier propiedad del sistema. Para la Energía libre
de Gibbs (G): M = G
( )
[ ] j
P,T,n
i
n
nG
μi ∂
∂
= (2.3)
Luego la ecuación (2.2) se puede expresar en función del μi
( ) ( ) ( ) ∑μ
+
−
= i
dn
i
dT
nS
dP
nV
nG
d (2.4)
Esta ecuación representa la relación fundamental entre propiedades
para sistemas de una sola fase con masa constante o variable y composición
constante o variable.
2.3.1. EL POTENCIAL QUÍMICO COMO UN CRITERIO DE EQUILIBRIO:
Consideremos un sistema cerrado formado por 2 fases en equilibrio
(P, T son uniformes en todo el sistema), en el cual cada fase individual es un
sistema abierto (transferencia de masa de una fase a otra), Fig. 2.1

12. 121
Fig. 2.1.- Sistema Cerrado en Equilibrio L-V.
Para cada fase en particular se escribe la Ecuación Energía Libre de
Gibbs para un sistema homogéneo de composición variable.
( ) ( ) ( ) ( )
[ ]
∑ ⋅
∂
∂
+
−
= i
n
,
T
,
P
i dn
n
nG
dT
nS
dP
nV
nG
d j
Fase α : d(nG)α
= (nV)α
dP – (nS)α
dT ∑ α
α
μ
+ i
i n
d
Fase α : d(nG)β
= (nV)β
dP – (nS)β
dT ∑ β
β
μ
+ i
n
d
i
Donde α y β identifican las fases.
El cambio total en la energía de Gibbs del sistema es la suma de las
ecuaciones anteriores. Toda propiedad total del sistema total se expresa con
una ecuación de la siguiente forma:
nM = (nM)α
+ (nM)β
Luego la Energía de Gibbs total del sistema.
d(nG) = d(nG)α
+ d(nVβ
)
( ) ( ) ( )
[ ] ( ) ( )
[ ] ∑ ∑ β
β
α
α
β
α
β
α
μ
+
μ
+
+
−
+
= i
i
i
i dn
dn
dT
nS
dT
nS
dP
nV
nV
nG
n
( ) ( ) ( ) ∑ ∑ β
β
α
α
μ
+
μ
+
−
= i
i
i
i dn
dn
dT
nS
dP
nV
nG
d

13. 122
Como el sistema difásico es cerrado, la ecuación
, también es válida en este caso.
( ) ( ) ( )dT
nS
dP
nV
nG
d −
=
La transferencia de masa entre fase produce cambios en el número
de moles de los componentes. Sin embargo lo que pierde una fase lo gana
la otra por lo general (Esto es porque hay equilibrio entre fases).
β
α
−
= i
i dn
dn
Por lo que ∑ ∑ =
μ
+
μ β
β
α
α
0
dn
dn i
i
i
i
Por lo que; ( )
∑ =
μ
−
μ α
β
α
0
dni
i
i
Se tiene; ⇒ (i = 1, 2, 3, … n)
0
i
i =
−
μ β
α β
α
μ
=
μ i
i
Donde: n = es el número de componentes presentes en el sistema.
Para mas de 2 fases (π fases)
=
μ
=
μ
=
μ π
β
α
i
i
i ... , ( )
n...
2,
1,
i = (2.5)
Se dice que dos o más fases (múltiples fases) están en equilibrio
cuando el potencial químico de cada componente es el mismo en todas las
fases.

14. 123
2.4. PROPIEDADES DE MEZCLAS (GASEOSAS Y LÍQUIDAS IDEALES:
2.4.1. MEZCLA DE GASES IDEALES:
Fig. 2.2.- Sistema cerrado mezcla gas ideal.
Cuando una mezcla de gas ideal ocupa un volumen total (V) a la
temperatura T. La presión es igual a: V
T
nR
P =
Si nk (moles del componente k) de esa mezcla ocupa el mismo
volumen (V) a la misma T, la presión resulta: V
RT
n
P k
k =
Dividiendo las dos ecuaciones anteriores: k
k
k y
n
n
P
P =
=
donde: yk: Fracción molar de componente k en la mezcla.
Pk: Presión parcial del componente k en la mezcla.
Luego resulta; P
y
P k
k ⋅
=
Ley de Dalton:
∑
= k
P
P (La suma de las presiones parciales es igual a la Presión
total P).

15. 124
TEOREMA DE GIBBS:
Una propiedad termodinámica total (nU, nH, nCp, nS, nA, nG) de una
mezcla gaseosa de gas ideal es igual a la suma de las propiedades totales
de los componentes individuales puros cada uno evaluado o la T de la
mezcla pero a su presión parcial. Esto es:
Un gas ideal es un modelo compuesto de moléculas imaginarias de
volumen nulo y sin interacción. En consecuencia cada compuesto químico
en una mezcla gaseosa ideal conserva sus propiedades sin verse alterado
por la presencia de otros componentes.
O sea, si M es una propiedad general de un gas ideal.
( ) ( )
∑ ⋅
⋅
⋅
= k
i
g
k
k
i
g
P
,
T
,
T
M
n
nM ρ dividiendo entre n
( )
∑ ρ
= ⋅
⋅
k
i
g
k
k
i
g
)
P
,
T
( T,
M
y
M (2.6)
Todas las propiedades del sistema pueden ser expresadas por este
Teorema.
Entalpía (H):
Como la entalpía de un gas ideal es independiente de la presión.
( ) ( P
,
T
H
p
,
T
H i
.
g
K
K
i
.
g
K = )

16. 125
Por lo que la ecuación (2.6) resulta:
∑ ⋅
⋅
= i
g
k
k
i
g
H
y
H (2.7)
donde se sobreentiende que Hg.i
y la son valores a T y a P de la
mezcla.
i
g
k
H ⋅
Lo mismo se aplica para Ug.i
y otras propiedades independientes de
la presión.
Cambio de Entalpia por Mezclado:
De la ecuación (2.7)
0
H
y
H i
g
k
i
i
g
=
− ⋅
⋅
(2.8)
Esta ecuación representa el cambio de entalpía por mezclado en un
proceso en el que cantidades apropiadas de componentes puros forman
1 mol de la mezcla a la misma (T, P) .
Para gas ideal este cambio en la entalpía por mezclado es igual a
cero.
Entropía (S):
Es una función de la presión para un gas ideal. Por definición de S
para un gas ideal:
( ) P
dP
R
T
dT
Cp
dS i
g
k −
=
⋅

17. 126
P
ln
Rd
dS i
g
k −
=
⋅
(T = cte)
La integración de Pk a P constante se obtiene
( ) ( ) k
k
i
g
k
i
g
p
P
ln
R
p
,
T
S
P
,
T
S −
=
− ⋅
⋅
, por lo tanto
k
k y
ln
R
P
y
P
ln
R =
⋅
−
=
( ) ( ) k
k
i
g
k
i
g
k y
ln
R
P
,
T
S
P
,
T
S =
− ⋅
⋅
( ) ( ) k
i
g
k
k
i
g
k y
ln
R
P
,
T
S
p
,
T
S −
= ⋅
⋅
Aplicando el teorema de Gibbs ∑ ⋅
⋅
= )
P
,
T
(
k
k
i
g
k
S
y
S escrito para la
entropía y sustituyendo el resultado de la ecuación anterior:
, resulta:
( ) K
i
.
g
K
K
i
.
g
K RLnY
S
p
,
T
S −
=
( )
∑ ∑
−
= ⋅
⋅
⋅
k
k
k
i
g
)
P
,
T
(
k
k
i
g
)
P
,
T
( y
ln
y
R
p
,
T
S
y
S k
o sencillamente
∑ ∑
−
= ⋅
⋅
k
k
i
g
k
k
i
g
y
Ln
y
R
S
y
S (2.9)
Donde Sg.i
y son valores a la T y P de la mezcla.
i
g
k
S ⋅
Cambio de entropía por mezclado:
∑ ∑
=
− ⋅
⋅
k
k
i
g
k
k
i
g
y
1
ln
y
R
S
y
S

18. 127
Esta ecuación representa el cambio de Entropía por mezclado para
gases ideales. Como 1/k > 1, el ΔS(gi)
siempre será > 0 (positivo). De
acuerdo a la Segunda Ley el proceso de mezclado para mezclas de gases
ideales a T, P constantes es irreversible y no se acompaña de transferencia
de calor.
Energía Libre de Gibbs: (Por definición)
G = H– TS
Para una mezcla de gas ideal se obtiene
Ggi
= Hg.i
– TSg.i
Si se sustituye en la ecuación (2.7) y (2.9).
∑ ∑ ∑
+
−
= ⋅
⋅
k
k
g
k
k
i
g
k
k
i
g
y
ln
y
RT
S
y
T
H
y
G
∑ ∑
+
= ⋅
⋅
k
k
i
g
k
k
i
g
y
ln
y
RT
G
y
G (2.10)
donde Gg.i
y son valores a T y P de la mezcla.
i
g
k
G ⋅
Potencial químico: ( µi)
El potencial químico del componente (i) de una mezcla de gas ideal se
expresa en función de la energía de Gibbs por la siguiente ecuación:
( )
[ ] j
n
,
T
,
P
i
i
g
i
g
i n
nG ∂
∂
=
μ ⋅
⋅
Multiplica la ecuación (2.10) por n:

19. 128
∑ ∑
+
= k
k
i
.
g
k
k
i
.
g
y
ln
n
RT
G
n
nG
Como n
n
y k
k = ⇒ n
y
n k
k ⋅
= entonces ∑
= k
n
n
Tenemos
n
Ln
n
RT
y
Ln
n
RT
G
n
nG k
k
k
i
.
g
n
k
i
.
g
∑
∑
∑ −
+
=
∑ ∑ −
+
= n
Ln
RTn
n
Ln
n
RT
G
n
nG k
k
i
.
g
k
k
i
.
g
donde:
k: Es el conjunto de todos los componentes de la mezcla
i: Es un componente particular de la mezcla
Si del conjunto de todos los componentes de la mezcla se separa el
componente i a ese conjunto se le llama j.
o sea ∑ ∑ ∑
∑ −
=
⇒
+
= i
k
j
i
j
k n
n
n
n
n
n
luego
∑ ∑ −
+
+
+
= n
Ln
n
RT
n
Ln
n
RT
n
Ln
n
RT
G
n
G
n
nG j
j
i
i
i
.
g
j
j
i
.
g
i
i
i
.
g
Aplicando el concepto del y diferenciando a P y T constantes, los
nj son constantes.
i
.
g
i
μ
( )
[ ] ( ) ( )
[ ]
j
j
j n
i
n
i
i
n
i
i
i
i
.
g
i
i
.
g
i n
n
ln
n
n
ln
n
RT
n
ln
n
n
ln
n
RT
G ∂
∂
+
∂
∂
−
+
∂
∂
+
=
μ
Como: y
∑
= k
n
n ∑ +
= i
j n
n
n

20. 129
Se tiene ( ) 1
n
n j
n
i =
∂
∂
n
n
ln
RT
G i
i
.
g
i
i
.
g
i +
=
μ
i
i
.
g
i
i
.
g
i y
ln
RT
G +
=
μ (2.11)
2.4.2. SOLUCIÓN IDEAL:
Modelo de comportamiento en el que las moléculas tienen el mismo
tamaño y todas las fuerzas entre las moléculas (semejantes y diferentes)
son iguales.
Las mezclas presentan interacciones atómicas o moleculares entre los
componentes cuya magnitud depende de la naturaleza de las sustancias y
de las condiciones a las cuales se encuentra. Para el caso de soluciones
líquidas ideales las fuerzas intermoleculares son casi iguales y simétricas.
Para el caso real las fuerzas intermoleculares son distintas y asimétricas.
Propiedades de una solución ideal:
Volumen (VSi
):
Por el teorema de Gibbs para un g.i tenemos:
∑
= g.i
i
i
.
g
V
y
V (2.12)

21. 130
Cuando se mezclan gases ideales no hay cambio de volumen por
mezclado debido a que el volumen molar de la mezcla (Vg.i
) es igual al (Vi)
volumen molar de los componentes puro a RT/P
V mezcla = V mezcla de gases ideales - V componentes puros
Volumen de la mezcla de gases ideales:
Por Gibbs: ∑
= i
.
g
i
i
i
.
g
V
y
V
Volumen de los componentes puros ∑
= i
i
i V
y
V = V
i
i
.
g
i V
V =
ΔV mezcla = 0 (2.13)
El cambio de volumen V mezclado para gases ideales es igual a cero.
Para una solución líquida ideal:
i
i
Si
V
X
V = (2.14)
Vs.i
: Volumen molar de la solución ideal.
Vi: Volúmenes molares del componente i puro a T y P de la mezcla.
Xi: Fracción molar del componente i en la fase líquida.
Cambio de volumen por mezclado para una solución ideal:
i
i
.
s
V
V
V −
=
Δ ; i
i
.
s
V
V =
ΔV mezclado = 0 (2.15)

22. 131
El volumen por mezclado para una solución ideal es igual a cero.
Como hay simetría a nivel de fuerzas intermoleculares, durante
la preparación de la mezcla a partir de los componentes puros a las
mismas condiciones, no se observan dilataciones o contracciones
macroscópicas.
El modelo de una solución ideal no produce cambio alguno en las
energías o volúmenes moleculares entonces se pueden escribir ecuaciones
análogas a las de modelo de un gas ideal.
Entalpía (Hs.i
):
i
i
i
.
s
H
X
H ∑
= donde Hi: Entalpía del componente puro (2.16)
Entropía (Ss.i
):
i
i
i
i
.
i
.
s
X
ln
X
R
S
X
S −
=
∑ (2.17)
Energía Libre de Gibbs (Gs.i
):
∑
∑ +
= i
i
i
i
i
.
s
X
ln
X
RT
G
X
G (2.18)
Potencial químico de un componente en la solución:
i
i
i
.
g
i X
ln
RT
G +
=
μ (2.19)

23. 132
La Si y Gi son propiedades de los componentes puros a T y P de la
mezcla.
Ejemplos de Soluciones líquidas ideales:
• Soluciones cuyas moléculas son de tamaño semejantes y de la misma
naturaleza química con frecuencia se comportan del mismo modo que la
solución ideal.
• Algunas mezclas de componentes molecularmente similares y no polares
se aproximan a este modelo. Ej. Soluciones de Benceno – Tolueno.
2.5. LEY DE RAOULT:
Supongamos que tenemos una fase líquida y una fase de vapor en
equilibrio a una T y P (ambas formadas por n componentes químicos)
La condición necesaria para que ambas fases coexistan en equilibrio
es que:
L
i
v
i μ
=
μ (i = 1, 2, … n)
Si consideramos comportamiento ideal de ambas fases.
i
L
i
i
i
.
g
i X
ln
RT
G
y
ln
RT
G +
+
+ rearreglando:
i
.
g
i
L
i
i
i G
G
X
y
ln
RT −
= (2.20)
O sea que las propiedades de los componentes puros se evalúan en el
equilibrio a la T y P de la mezcla en equilibrio.

24. 133
Despreciando el efecto de la presión sobre L
i
G
( ) ( )
sat
i
L
i
L
i P
,
T
G
P
T,
G = (2.21)
Donde: Es la presión de vapor o de saturación del componente i puro
a la Temperatura T.
:
Psat
i
Para un gas ideal constituido por un componente puro:
dG = VdP - S dT
dT
S
dP
V
dG i
.
g
i
.
g
i
i
.
g
i −
= (T = cte)
Integrando desde P hasta a la temperatura T
sat
i
P
( ) ( ) P
dP
RT
P
,
T
G
P
,
T
G
sat
i
P
P
i
.
g
i
sat
i
i
.
g
i ∫
=
−
( ) ( ) P
P
ln
RT
P
,
T
G
P
,
T
G sat
i
i
.
g
i
sat
i
i
.
g
i =
−
( ) ( ) P
P
ln
RT
P
,
T
G
P
,
T
G sat
i
sat
i
i
.
g
i
i
.
g
i +
= (2.22)
Sustituyendo la ecuación (2.21) y (2.22) en la ecuación (2.20)
( ) P
P
ln
RT
G
P
,
T
G
x
y
ln
RT sat
i
i
.
g
i
sat
i
L
i
i
i +
−
=
donde: : son la energía de Gibbs para el líquido puro y el
vapor puro del componente (i) a las condiciones de equilibrio
del componente puro a (T, .
L
i
G y i
.
g
i
G
sat
i
P )
En el equilibrio: i
.
g
i
L
i G
G =

25. 134
Resulta:
P
P
ln
RT
x
y
ln
RT sat
i
i
i = P
P
x
y sat
i
i
i ⇒
sat
i
i
i P
x
P
Y = Ley de Raoult (i – 1, 2, … n) (2.23)
donde:
P: presión del sistema.
sat
i
P : presión de vapor de los componentes puros.
Xi: fracción molar del componente (i) en la fase líquida.
Yi: tracción molar del componente (i) en fase de vapor.
Ley de Raoult
La expresión (2.23) representa la ecuación para la Ley de Raoult, la
cual establece lo siguiente: La presión parcial del componente (i) en la fase
gaseosa es igual al producto de la fracción molar del componente (i) en la
fase líquida por su presión de vapor a la temperatura T.
2.6. EQUILIBRIO LÍQUIDO – VAPOR. SISTEMAS BINARIOS:
Si la fase líquida es ideal y además la fase gaseosa está formada por
una mezcla binaria de gases ideales (i = 1,2).
2
1
2
1
p
p
y
y y1 , y2 : Fracción molar de 1 y 2 en el gas.
P1 , P2: Presión parcial de 1 y 2 en el gas.
2
1
2
1
P
P
x
x X1 , x2 : Fracción molar de 1 y 2 en el líquido.
P1 , P2 : Presión de vapor de 1 y 2 líquido puros.
Fig. 2.3.- Equilibrio líquido-vapor de una mezcla binaria ideal.

26. 135
Aplicando Ley de Raoult.
sat
i
i
i P
x
P
y = (i = 1,2)
donde o sea que la Pi proporcional a xi.
sat
i
i
i
i
i P
x
P
P
y
P =
⇒
=
Para sistemas binarios:
Comp (1) Y1 P = X1 P1
Sat
Comp (2) Y2 P = X2 P1
Sat
.
Y1+Y2 P = X1P1
Sat
+ X2 P2
Sat
Como ⇒
1
Y
Y 2
1 =
+ sat
2
2
sat
1
1 P
X
P
X
P +
= (2.24)
Además X1 + X2 = 1 X2 = 1 – X1
luego: ( ) sat
2
1
sat
1
1 P
X
1
P
X
P −
+
=
( ) 1
sat
2
sat
1
sat
2 X
P
P
P
P −
+
= (2.25)
Presión total del sistema en función de la composición de la fase
líquida:
La ecuación (2.25) representa la presión total del sistema en función
de la composición de la fase líquida. Fig. 2.4.
sat
1
1
1 P
X
p =
P
P
P
1
x sat
1
1
1 =
=
⇒
=
sat
2
2
2 P
X
p =
P
P
p
1
x sat
2
2
2 =
=
⇒
=
Fig. 2.4. Presión Total de un sistema binario vs
la composición de la fase líquida i (Xi) ∑
= i
p
P Ley de Daltón

27. 136
Presión Total en Función de la Fase de Vapor:
( ) 1
sat
2
sat
1
sat
2 X
P
P
P
P −
+
=
Tenemos: ⇒
sat
1
1
1 P
X
P
Y = sat
1
1
1 P
P
Y
X =
( ) ( ) sat
1
1
sat
2
sat
1
sat
2 P
P
Y
P
P
P
P ⋅
−
+
=
( )
( ) sat
1
1
sat
2
sat
1
sat
2
sat
1 P
P
Y
P
P
P
P
P −
+
=
( ) P
Y
P
P
P
P
P
P 1
sat
2
sat
1
sat
2
sat
1
sat
1 −
+
=
( ) sat
2
sat
1
1
sat
2
sat
1
sat
1 P
P
P
Y
P
P
P
P =
−
−
( )
[ ] sat
2
sat
1
1
sat
1
sat
2
sat
1 P
P
Y
P
P
P
P =
−
+
( ) 1
sat
1
sat
2
sat
1
sat
2
sat
1
Y
P
P
P
P
P
P
−
+
= (2.26)
En la ecuación (2.26) se observa que P no varía linealmente con la
composición en la fase de vapor.
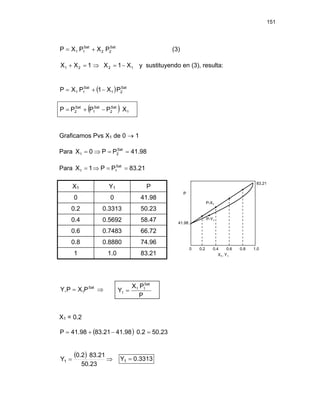
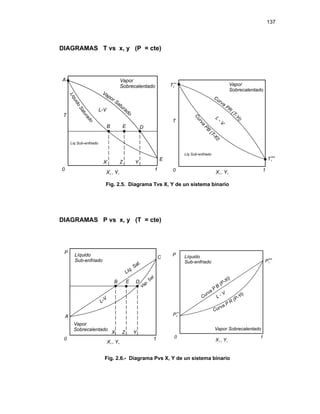
2.6.1. DIAGRAMAS DE FASES DE SISTEMAS BINARIOS:
El comportamiento de fases de sistemas binarios (i = 1,2) puede
representarse mediante diagramas Fig. 2.5 ; Fig. 2.6.
Estos diagramas generalmente se utilizan para ilustrar los estados de
mezclas binarias.
y
x,
vs
T y
x,
vs
P
Los diagramas: T vs x, y son a P = cte y
P vs x, y son a T = cte

28. 137
DIAGRAMAS T vs x, y (P = cte)
Fig. 2.5. Diagrama Tvs X, Y de un sistema binario
DIAGRAMAS P vs x, y (T = cte)
Fig. 2.6.- Diagrama Pvs X, Y de un sistema binario

29. 138
• Estas dos curvas PR (Puntos de Rocío) y PB (Puntos de Burbuja),
convergen en los valores de saturación del componente puro sobre los
ejes T y P en los extremos ; X = 0, X = 1.
• En el Diagrama T – x,y las T de los extremos corresponden a los
valores de las T sat de los componentes puros (T de ebull a P = cte).
• En el Diagrama P – x,y las presiones de los extremos representan
presiones de vapor de los componentes puros a (T = cte).
• La región por debajo de la curva de Punto de Burbuja en un diagrama
T – x, y y por encima de la curva de Punto de Burbuja en un diagrama
P – x,y corresponde a estados de líquido sub-enfriado.
• La región por encima de la curva del Punto de Rocío en un diagrama
T – x,y y por debajo de la curva de Punto de Rocío en un diagrama
P – x, y corresponde a los estados de vapor sobrecalentado.
• El área entre ABC y ADC en ambos diagramas es la región de 2 fases
líquido-vapor.
• Las mezclas cuyas coordenadas (T, x) o (P, x) están dentro de esta
área, se separan espontáneamente en una fase de vapor y una fase
líquida. Las composiciones de equilibrio de las fases formadas durante la
separación se determinan en los diagramas de fases mediante la
intersección de la recta horizontal T ó P con las curvas del PR y PB.

30. 139
• El intervalo de T está limitado por las temperaturas de saturación T1,Sat
y T2
Sat
a los cuales los componentes puros ejercen presiones iguales a
la presión de vapor P.
sat
1
sat
1
1
1 P
P
P
X
P
Y =
⇒
= @ ;
sat
1
T 1
Y
X 1
1 =
=
sat
2
sat
2
2
2 P
P
P
X
P
Y =
⇒
= @ ;
sat
2
T 1
Y
X 2
2 =
=
• En ambas figuras T vs X, Y ; P vs X,Y:
La curva ABC: representa los estados de mezclas de líquidos saturados,
se le llama curva de Punto de Burbuja.
La curva ADC: representa los estados de vapor saturado, se le llama
curva de los puntos de rocío.
REGLA DE LA PALANCA:
Para completar el estudio de los sistemas binarios se va a deducir una
regla que permite establecer cual es la razón entre la cantidad de masa
contenida en cada una de las fases en equilibrio.
Una mezcla de fracción molar Z a una Temp T y Presión P (Punto
E) en los diagramas T – x,y Fig. 2.5 o P – x,y Fig. 2.6; forma un líquido que
contiene una fracción molar x (punto B) y un vapor de fracción molar Y
(punto D).

31. 140
Las líneas rectas BD que conectan estados en equilibrio se les llama
líneas de enlaces.
Si la mezcla contiene n (moles) que tiene una fracción molar Z1 del
comp (1). La cual se separa en nL (moles de líquido con fracción molar X1)
y nV (moles de vapor de fracción molar Y1).
Un balance del número de moles del componente (1)
Z1 n = X1 nL + Y1 nV
Balance de moles totales:
n = nL + nV
(nL + nV) (Z1) = x1 nL + y1 nV
nL Z1 + nV Z1 = x1 nL + y1 nV
nL Z1 – X1 nL = y1 nV – nV Z1
nL (Z1 – X1) = nV (Y1 – Z1)
( ) ( ) BE
ED
X
Z
Z
Y
n
n 1
1
1
1
V
L =
−
−
= Regla de la Palanca (2.27)
La ecuación (2.27), establece que los números de moles de las fases
en equilibrio es inversamente proporcional a la relación de las longitudes de
los correspondientes segmentos de las líneas de enlace.
CONSTRUCCION DE UN DIAGRAMA ELV:
La forma habitual de trazar un diagrama de fases líquido-vapor
consiste en medir previamente el mayor número de puntos experimentales y

32. 141
trazar entre ellos una curva de interpolación. Sin embargo, tampoco puede
desecharse a priori la idea de conocer tales diagramas a partir de
consideraciones de carácter teórico, ya que en muchos problemas de
ingeniería, el diseño de una columna de destilación presupone el estudio de
un diagrama de fases sin que se disponga de información previa al respecto.
Generalmente los diagramas de equilibrio para mezclar binarias se
construyen a partir de datos de equilibrio. En la tabla B1 (Anexo B) aparecen
algunos datos de equilibrio para ciertas sustancias.
Ejercicio:
Cálculo de curvas de equilibrio a partir de datos T, X, Y.
Dibuje las gráficas de las curvas T vs Xa, Yax
y Xa vs Yax
utilizando
la siguiente data:
T Xa Ya*
ºF % Molar % Molar
227.0 100.00 100.00
232.0 77.60 94.10
236.5 64.00 89.70
242.9 50.70 83.23
248.4 37.80 74.60
255.4 25.00 60.20
262.0 12.40 34.50
265.0 0.00 0.00
Ejercicio:
Cálculo de curvas de equilibrio a partir de datos T, X, T.

33. 142
Resultado:
Ejemplo de Curva de Equilibrio T vs X, Y*
Ejemplo de Curva de Equilibrio X vs Y*

34. 143
2.6.2. CÁLCULO DEL PUNTO DE BURBUJA (PB) Y PUNTO DE
ROCÍO (PR):
• Punto de Burbuja (PB):
El punto de burbuja de una mezcla a T y P viene dada por la siguiente
condición: 1
Yi =
∑
Determinación de PB, TB y Yi.
A partir de datos: T = cte, P cte, Xi
Partiendo de la condición ∑ = 1
Yi
Para sistemas ideales (Ley de Raoult):
P
P
X
Y
P
X
P
Y
sat
i
i
i
sat
i
i
i =
⇒
=
Por definición la constante de equilibrio es igual a:
P
P
K
X
Y
K sat
i
i
i
i
i =
⇒
=
Luego:
∑ = 1
P
P
X
sat
i
i (2.28)
donde:
Ki = Constante de equilibrio de i a la T y P de la mezcla.
Xi = Fracción molar de i en la fase líquida.
Punto de Burbuja: Se define como la P o la T a la cual se forma
la primera gota de vapor cuando un líquido se dilata (P = PB) o se calienta
(T = TB) a T o P = cte respectivamente

35. 144
B
sat
i
i P
P
P
X =
=
∑ (2.29)
• Punto de Rocío (PR):
El punto de rocío de una mezcla a T y P, viene dado por la siguiente
condición: ∑ .
= 1
Xi
Determinación de PR, TR y Xi
A partir de: T cte, P cte, Yi
Partiendo de la condición ∑ = 1
Xi
sat
i
i
i P
P
Y
X = ; Para sistemas ideales P
P
K sat
i
i =
Luego: 1
P
P
Y
n
1
i
sat
i
i =
∑
=
(2.30)
Presión de Rocío: Se define como la P o la T a la cual se forma la
primera gota de rocío cuando un vapor se comprime (P = PR) o se enfría
(T = TR) a T o P cte respectivamente.
∑
=
= sat
i
i
R
P
Y
1
P
P (2.31)
2.6.3. CÁLCULO DE VAPORIZACIÓN INSTANTÁNEA (Flash):
Constante de Equilibrio (KI):
La aplicación principal del equilibrio de fases, se encuentra en el
diseño de procesos de separación que dependen de la tendencia de una

36. 145
especie química dada a distribuirse en una u otra fase de equilibrio. Una
medida apropiada de esta tendencia con respecto al equilibrio V-L viene
dada por la siguiente relación:
i
i
i X
Y
K = (2.32)
Ki: generalmente se le denomina coeficiente de reparto o constante de
equilibrio.
Si Ki > 1 ⇒ que el componente (i) tiende a concentrarse en la fase de vapor
y se dice que el componente es liviano, y la fase de vapor es
rica en este componente.
Si Ki < 1⇒ que el componente (i) se concentra en la fase líquida y se
considera entonces como pesado y la fase líquida es rica en
este componente.
De Raoult tenemos: sat
i
i
i P
X
P
Y =
P
P
X
Y sat
i
i
i = o sea P
P
K sat
i
i = (2.33)
Esta ecuación solo es válida para sistemas ideales, más adelante se
explicará como determinar esta corriente en el caso de sistemas reales.
El cálculo de vaporización instantánea consiste en la determinación
de las composiciones yi, xi y cantidades de las fases líquidas y vapor

37. 146
(L y V) en equilibrio a partir de la P yT y composición Zi de la corriente de
alimentación. En la Fig. 2.7, se representa este proceso.
F (Zi)
V (Yi)
L (Xi)
P1
P > P
1 B
P2
Líquido
Separador
Vapor
Mezcla
Líquida
Mezcla
(L-V)
Una mezcla líquida cuya P1 > a su
PB podría evaporarse
instantáneamente si su presión
desciende a una presión P2 que
este comprendía entre la PB y PR.
Fig. 2.7.- Sistema de Vaporización Instantánea.
Tal proceso puede realizarse continuamente si un líquido (F) se
estrangula a través de una válvula de expansión en un tanque a una P dada
produciéndose una separación de ambas fases líquida (L) y vapor (V) a una
P y T particulares, donde las corrientes del proceso F, L y V se pueden
expresar por unidad de masa o mol.
Procedimiento para determinar L, V, Xi, Yi
− Balance Global: F = L + V.
Considerando Base de cálculo: F = 1 mol de mezcla de composición (Zi)
1 = V + L ⇒ V
1
L −
= (2.34)

38. 147
− Balance de componente:
( ) V
Y
V
1
X
Z i
i
i +
−
= (i = 1, 2, … n) (2.35)
Sustituyendo Xi = Yi/ Ki en la ecuación (2.35)
Zi = Yi/Ki (1 – V) + Yi (V)
Zi = (Yi (1-V) + Yi V Ki)/Ki
Zi Ki = Yi (1 – V) + Yi V Ki
Zi Ki = Yi – Yi V + Yi V Ki ⇒ Zi Ki = Yi [1+V (Ki –1)]
Despejando Yi
( ) ( )
1
K
V
1
K
Z
Y i
i
i
i −
+
= (2.36)
Como la condición del Punto de Burbuja ∑ = 1
Yi
( ) ( )
∑ −
+ 1
K
V
1
K
Z i
i
i (2.37)
En la ecuación (2.37) se determina V por ensayo y error hasta que se
cumpla la condición.
Luego de (2.34) se obtiene L, y de (2.36) se calcula Yi
Los Ki se obtiene de la ecuación: P
P
K sat
i
i =
Luego como i
i
i X
Y
K = ⇒ i
i
i K
Y
X = (2.38)

39. 148
De esta ecuación se obtiene Xi .
El cálculo de vaporización instantánea es correcto si se satisfacen la
condición del punto de rocío y punto de burbuja ∑ i
X y
respectivamente.
∑ = 1
Yi
En la región difásica L y V deben ser:
0 ≤ L ≤ 1
0 ≤ V ≤ 1
Estas desigualdades se satisfacen si la T y P están dentro del
intervalo en el cual puede existir un sistema de 2 fase de la región difásica.
Un sistema difásico a una T dada y una composición promedio Zi
puede existir dentro de un amplio intervalo de presiones.
− Desde el punto de burbuja (PB); donde V = 0 y L = 1 ⇒ Zi = Xi
La expresión ( ) ( )
∑ =
−
+ 1
1
K
V
1
K
Z i
i
i
Se transforma en ∑ = 1
K
Z i
i
Donde:
Zi: Es equivalente a la composición del líquido saturado Xi ( )
i
i X
Z =
La condición es ∑
= sat
i
i
B P
Z
P

40. 149
− Hasta el punto de Rocío Pr; donde V = 1 y L = 0 ⇒ Zi = Yi
En este caso la expresión:
∑
= sat
i
i
R P
Y
1
P Se transforma en: ∑
= sat
i
i
R P
Z
1
P
donde: Zi: Es equivalente a la composición del vapor saturado
Yi (Zi = Yi)

41. 150
EJEMPLOS ILUSTRATIVOS
Ejemplo 2.1. Construcción de Diagrama de ELV
El sistema binario Acetileno (1) / Nitrometano (2) concuerda bastante
con la Ley de Raoult. La presión de vapor de los componentes puros está
dada por las siguientes ecuaciones de Antoine:
( )
( ) 224
C
º
T
2945.47
-
14.2724
kPa
P
Ln Sat
1
+
=
( )
( ) 209
C
º
T
2972.64
2043
.
14
kPa
LnPSat
2
+
−
=
Prepare un gráfico que muestre P en función de X1 y P en función de Y1
para T de 75 ºC.
Solución:
a 75 ºC sustituyendo en la ecuación
kPa
.21
83
1 =
Sat
P
kPa
98
.
41
PSat
2 =
Para cada uno de los componentes (i) tenemos: Sat
i
i
1 P
X
P
Y =
Sat
1
1
1 P
X
P
Y = (Comp 1) (1)
Sat
2
2
2 P
X
P
Y = (comp. 2) (2)
como Y1 + Y2 = 1 ⇒ la suma de (1) y (2)

42. 151
Sat
2
2
Sat
1
1 P
X
P
X
P +
= (3)
1
X
X 2
1 =
+ ⇒ y sustituyendo en (3), resulta:
1
2 X
1
X −
=
( ) Sat
2
1
Sat
1
1 P
X
1
P
X
P −
+
=
( ) 1
Sat
2
Sat
1
Sat
2 X
P
P
P
P −
+
=
Graficamos Pvs X1 de 0 → 1
Para 41.98
P
P
0
X Sat
2
1 =
=
⇒
=
Para 83.21
P
P
1
X Sat
1
1 =
=
⇒
=
X1 Y1 P
0 0 41.98
0.2 0.3313 50.23
0.4 0.5692 58.47
0.6 0.7483 66.72
0.8 0.8880 74.96
1 1.0 83.21
Sat
1P
X
P
Y, = ⇒
P
P
X
Y
Sat
1
1
1 =
X1 = 0.2
( ) 50.23
0.2
41.98
83.21
41.98
P =
−
+
=
( ) ⇒
=
50.23
83.21
0.2
Y1 3313
.
0
Y1 =

43. 152
Ejemplo 2.2: Cálculo de Presión de Burbuja (PB) y Presión de Rocío (PR).
Para un sistema Acetona (1) / Acetonitrilo (2) / Nitrometano (3), se
tienen las siguientes ecuaciones de Antoine:
237.22
T
2940.46
14.5463
P
Ln Sat
1
+
−
=
224.0
T
2945.47
14.2724
P
Ln Sat
2
+
−
=
209
T
2972.64
14.2043
P
Ln Sat
3
+
−
=
Donde T está en (ºC) y la presión de
vapor en kPa, considere
comportamiento ideal del sistema.
Determine:
a) PB YK, dado T = 80 ºC, X1 = 0.25, X2 = 0.35, X3 = 0.40
b) PR XK, dado T = 70 ºC, Y1 = 0.50, Y2 = 0.30, X3 = 0.20
Solución:
a) Punto de Burbuja:
1
Yi =
∑
Raout: Sat
i
i
i P
X
P
Y =
P
P
X
Y
Sat
i
i
i =
∑ = 1
P
P
X Sat
i
i
∑
= Sat
i
i P
X
P

44. 153
Se evaluan las C
º
80
PSat
i usando las Relaciones de Antoine del
Problema:
kPa
195.75
PSat
1 =
kPa
97.84
PSat
2 =
kPa
50.32
PSat
3 =
Luego
( )( ) ( )( ) ( )( )
50.32
0.40
97.84
0.35
195.75
0.25
P +
+
=
kPa
103.31
P = = PB
Cálculo de los Yi:
P
P
X
Y
Sat
i
i
i =
Y1 = 0.4737
Y2 = 0.3315
Y3 = 0.1948

45. 154
b) Punto de Rocío Xi
La condición ∑ = 1
Xi
Sat
i
i
i P
X
P
Y =
Sat
i
i
i
P
P
Y
X =
1
P
P
Y
Sat
i
i
=
⋅
∑
∑
=
Sat
i
i
P
Y
1
P
P = PR
Se evalúan C
º
70
PSat
i en las ecuaciones:
kPa
43.80
P
70.37;
P
144.77;
P Sat
3
Sat
2
Sat
1 =
=
=
Sustituyendo los Yi del problema
PR = 74.27 kPa
Cálculo de los Xi:
Sat
i
i
i
P
P
Y
X =
X1 = 0.2569
X2 = 0.3166
X3 = 0.4269

46. 155
Ejemplo 2.3: Cálculo de Vaporización Instantánea.
El sistema acetona (1) / Acetileno / Acetonitrilo (2) / Nitrometano (3), a
80 ºC y 100 kPa, tiene una composición promedio de Z1 = 0.45, Z2 = 0.35 y
Z3 = 0.20. Determine L, V, Xi e Yi.
Solución:
Antes de hace el cálculo de evaporización instantánea.
1. Se debe comprobar para las condiciones establecidas, que el sistema
esté realmente en la región difásica.
2. Un sistema difásico a una T y Zi conocida puede existir dentro de un
amplio intervalo de presiones, desde PB donde V = 0 y Zi = Xi hasta el Pr
donde V = 1 y Zi = Yi.
Sat
P2
Sat
P1
P
X , Y
i i
Vapor Sobrecalentado
L - V
PB
PR
P-X i
P-Yi
Líquido
Sub-enfriado
Pto. Burbuja
Pto. Rocío
0 1
3. Si la P esta entre PB y PR el sistema es difásico.

47. 156
Las presiones de vapor para cada componente a 80 ºC
( )
kPa
50.23
P
97.84;
P
195.75;
P Sat
3
Sat
2
Sat
1 =
=
=
− Determinación de la PB
Condición del Punto de Burbuja ∑
= Sat
i
i P
X
P P = PB
∑ = 1
Yi
Sat
3
3
Sat
2
2
Sat
1
1
B P
X
P
X
P
X
P +
+
=
( )( ) ( )( ) ( )( )
50.32
0.20
97.84
0.35
195.75
0.45
PB +
+
=
kPa
132.40
PB =
− Determinación de la PR
Condición es ∑ = 1
Xi
∑
= Sat
i
i P
Y
1
P ; P = PR
Sat
3
3
Sat
2
2
Sat
1
1
R
P
Y
P
Y
P
Y
1
P
+
+
=
50.32
0.20
97.84
0.35
195.75
0.45
1
PR
+
+
=
PR = 101.52 kPa como PR < P < PB
El sistema es difásico

48. 157
Cálculo de V y L:
Cálculo de V:
( )
1
1
k
V
1
k
Z
i
i
i
=
−
+
∑
P
P
k
Sat
i
i =
110
19.75
ki = ⇒ k1 = 1.7795
k2 = 0.8895
k3 = 0.4575
( )( ) ( )( ) ( )( ) 1
V
5425
.
0
1
4575
.
0
20
.
0
V
1105
.
0
1
8895
.
0
35
.
0
V
0.7795
1
1.7795
0.45
=
−
+
−
+
+
se asumen valores de V hasta que se cumpla la igualdad.
. V = 0.7364 mol
Cálculo de L:
L = 1 – V = 1 – 0.7364
⇒ . L = 0.2636 mol
Cálculo de Yi , Xi
( )
1
k
V
1
k
Z
Y
i
i
i
i
−
+
=
∑ = 1
i
Y
Y1 = 0.5087
Y2 = 0.3389
Y3 = 0.1524
i
i
i
k
Y
X =
X1 = 0.2859
X2 = 0.3810
X3 = 0.331
Se cumple:
1
=
= ∑
∑ i
i X
Y

49. 158