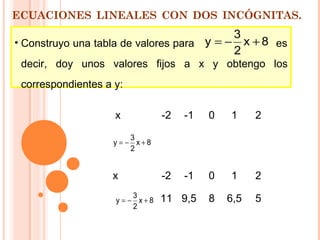
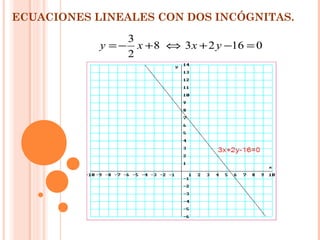
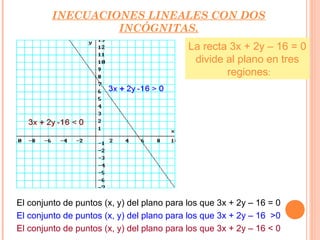
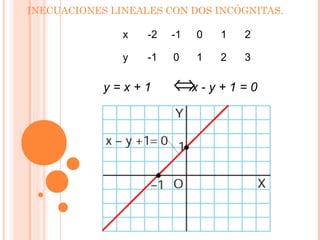
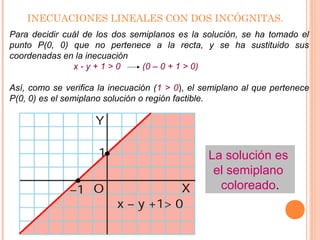
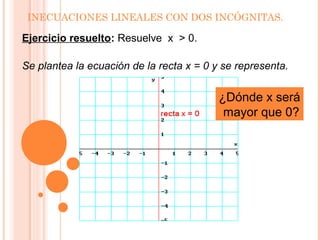
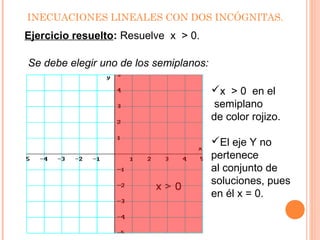
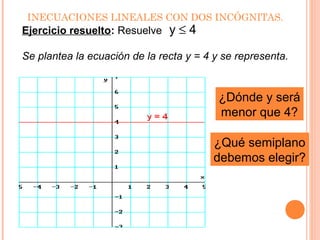
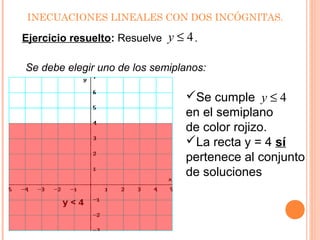
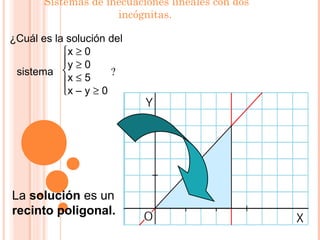
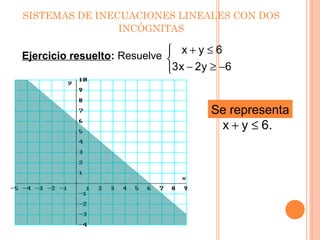
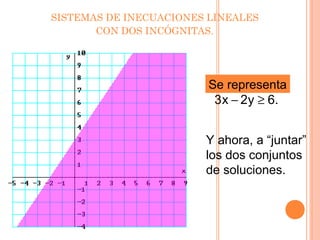
Este documento presenta información sobre inecuaciones lineales y sistemas de inecuaciones lineales con dos incógnitas. Explica que una inecuación lineal divide el plano en dos semiplanos, y que la solución es uno de esos semiplanos. También describe cómo resolver sistemas de inecuaciones lineales encontrando la intersección de las soluciones de cada inecuación, la cual puede ser un recinto poligonal o abierto. Incluye ejemplos resueltos de inecuaciones y sistemas de inecuaciones lineales.

1. TEMA.-
•Inecuaciones lineales con dos incógnitas.
•Sistemas de inecuaciones lineales con dos
incógnitas.
INECUACIONES LINEALES Y SISTEMAS
DE INECUACIONES LINEALES CON DOS
INCÓGNITAS
SILVIA MARTÍNEZ RAMÍREZ

2. INTRODUCCIÓN:
ECUACIONES LINEALES CON DOS INCÓGNITAS
• Recuerda que una ecuación lineal con dos incógnitas
como 3x+ 2y–16 = 0 representa gráficamente una
recta, la cual vimos que se representaba así:
•Despejo la letra y en 3x + 2y – 16 = 0:
8x
2
3
2
x316
y +−=
−
=
• Construyo una tabla de valores para es
decir, doy unos valores fijos a x y obtengo los valores
correspondientes a y.
8x
2
3
y +−=

3. ECUACIONES LINEALES CON DOS INCÓGNITAS.
x -2 -1 0 1 2
x -2 -1 0 1 2
11 9,5 8 6,5 5
• Construyo una tabla de valores para es
decir, doy unos valores fijos a x y obtengo los
correspondientes a y:
8x
2
3
y +−=
8x
2
3
y +−=
8x
2
3
y +−=

4. ECUACIONES LINEALES CON DOS INCÓGNITAS.
016238
2
3
=−+⇔+−= yxxy

5.  El conjunto de puntos (x, y) del plano para los que ax + by + c
= 0 (recta).
 El conjunto de puntos (x, y) del plano para los que ax + by + c
> 0 (semiplano).
 El conjunto de puntos (x, y) del plano para los que ax + by + c
< 0 (semiplano).
INECUACIONES LINEALES CON DOS INCÓGNITAS
Toda recta ax + by + c = 0 divide al plano en tres regiones:

6. INECUACIONES LINEALES CON DOS
INCÓGNITAS.
La recta 3x + 2y – 16 = 0
divide al plano en tres
regiones:
El conjunto de puntos (x, y) del plano para los que 3x + 2y – 16 = 0
El conjunto de puntos (x, y) del plano para los que 3x + 2y – 16 >0
El conjunto de puntos (x, y) del plano para los que 3x + 2y – 16 < 0

7. INECUACIONES LINEALES CON DOS INCÓGNITAS.
 Así pues, una inecuación lineal con dos incógnitas adopta una de
estas formas: ax + by + c > 0 ó ax + by + c < 0
En vez de los signos < ó >, puede tener
 En cada una de ellas, el conjunto de soluciones es el semiplano que
está a cada uno de los lados de la recta ax + by + c = 0.
Cuando en la desigualdad está incluido el igual ( ), los puntos de
la recta son también soluciones.
 A la parte del plano que es solución de una inecuación se le llama
región factible de la inecuación.
.ó ≥≤
≥≤ ó

8. INECUACIONES LINEALES CON DOS INCÓGNITAS.
Se toma un punto P(x,y)
cualquiera que no
pertenezca a la recta, y
se sustituyen sus
coordenadas en la
inecuación.
Si la verifican, el
semiplano al que pertenece
P es el semiplano solución
o región factible.
En caso contrario (que las
coordenadas de P no
verifican la inecuación), la
solución será el otro
semiplano.
 Para decidir cuál es la solución de los dos semiplanos :

9. INECUACIONES LINEALES CON DOS INCÓGNITAS.
x -2 -1 0 1 2
y -1 0 1 2 3
Ejercicio resuelto: Resuelve x – y + 1 > 0:
1. Se plantea la ecuación de la recta x - y + 1 = 0 y se
despeja la y: y = x + 1
2. Se construye una tabla de valores y se representa dicha
recta

10. INECUACIONES LINEALES CON DOS INCÓGNITAS.
x -2 -1 0 1 2
y -1 0 1 2 3
y = x + 1 ⇔x - y + 1 = 0

11. INECUACIONES LINEALES CON DOS INCÓGNITAS.
Para decidir cuál de los dos semiplanos es la solución, se ha tomado el
punto P(0, 0) que no pertenece a la recta, y se ha sustituido sus
coordenadas en la inecuación
x - y + 1 > 0 (0 – 0 + 1 > 0)
Así, como se verifica la inecuación (1 > 0), el semiplano al que pertenece
P(0, 0) es el semiplano solución o región factible.
La solución es
el semiplano
coloreado.

12. INECUACIONES LINEALES CON DOS INCÓGNITAS.
Ejercicio resuelto: Resuelve x > 0.
Se plantea la ecuación de la recta x = 0 y se representa.
¿Dónde x será
mayor que 0?

13. INECUACIONES LINEALES CON DOS INCÓGNITAS.
Ejercicio resuelto: Resuelve x > 0.
Se debe elegir uno de los semiplanos:
x > 0 en el
semiplano
de color rojizo.
El eje Y no
pertenece
al conjunto de
soluciones, pues
en él x = 0.

14. INECUACIONES LINEALES CON DOS INCÓGNITAS.
Ejercicio resuelto: Resuelve
Se plantea la ecuación de la recta y = 4 y se representa.
¿Dónde y será
menor que 4?
4y ≤
¿Qué semiplano
debemos elegir?

15. INECUACIONES LINEALES CON DOS INCÓGNITAS.
Ejercicio resuelto: Resuelve .
Se debe elegir uno de los semiplanos:
Se cumple
en el semiplano
de color rojizo.
La recta y = 4 sí
pertenece al conjunto
de soluciones
4≤y
4≤y

16. SISTEMAS DE INECUACIONES LINEALES
CON DOS INCÓGNITAS.
Una inecuación lineal con dos incógnitas adopta una de
estas formas: ax + by + c > 0 ó ax + by + c < 0
En vez de los signos < ó >, puede tener
Varias inecuaciones lineales forman un sistema cuando se
buscan soluciones comunes a todas ellas.
Como el conjunto de soluciones de una inecuación lineal
con dos incógnitas es un semiplano, el conjunto de
soluciones, si existe, será la intersección, si existe, de varios
semiplanos, es decir, un recinto poligonal o bien un
recinto abierto.
Si los semiplanos no tienen ningún punto en común, el
sistema no tiene solución y decimos que es incompatible.
≥≤ ó

17. Sistemas de inecuaciones lineales con dos
incógnitas.
x ≥ 0
y ≥ 0
x = 5
x ≤ 5
x – y = 0
x – y ≥ 0
¿Cuál es la solución del
sistema




x ≥ 0
y ≥ 0
x ≤ 5
x – y ≥ 0
?
La solución es un
recinto poligonal.

18. SISTEMAS DE INECUACIONES LINEALES CON DOS
INCÓGNITAS
Ejercicio resuelto: Resuelve



−≥−
≤+
6y2x3
6yx
Se representa
.6yx ≤+

19. SISTEMAS DE INECUACIONES LINEALES
CON DOS INCÓGNITAS.
Se representa
.6y2x3 ≥−
Y ahora, a “juntar”
los dos conjuntos
de soluciones.

20. SISTEMAS DE INECUACIONES LINEALES CON DOS
INCÓGNITAS.
Para “juntar” los dos conjuntos
de soluciones,
en unos mismos ejes de
coordenadas coloreamos de
colores distintos cada solución
de cada inecuación y, así, la
solución del sistema será la
región doblemente coloreada.
La solución es un recinto
abierto.
¡AHÍ ESTÁ!