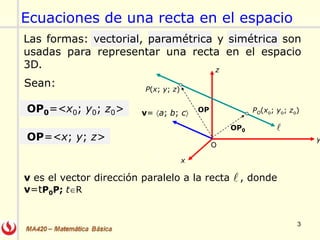
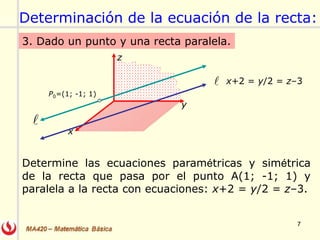
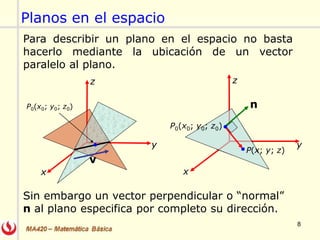
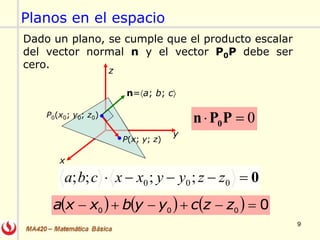
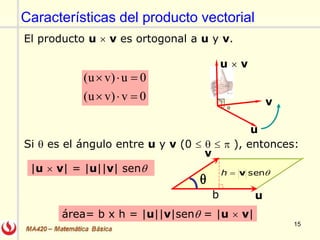
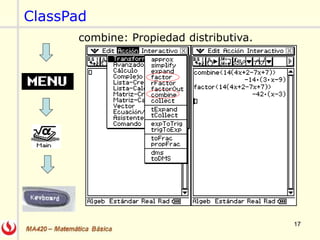
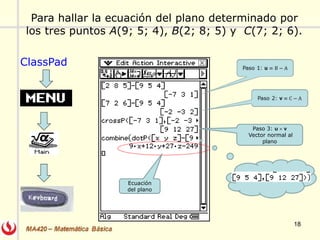
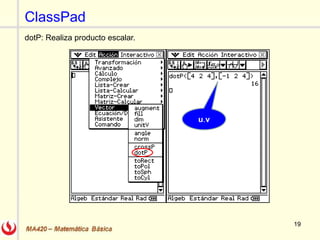
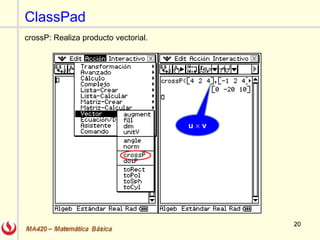
El documento describe las rectas y planos en el espacio tridimensional (R3). Explica cómo representar rectas utilizando formas vectoriales, paramétricas y simétricas, y cómo encontrar las ecuaciones de una recta dados diferentes puntos y vectores. También explica cómo encontrar la ecuación de un plano dado un punto y vector normal o tres puntos, utilizando el producto escalar y vectorial. Finalmente, enumera algunos ejercicios relacionados incluidos en un libro de cálculo.

1. 1
Espacio tridimensional (3D)
Planos y rectas en R3
Sesión 15.1

2. 2
Planos y rectas en R3
 Rectas en el espacio y sus formas de representar.
 Planos en el espacio y sus ecuaciones.
 Productos vectoriales

3. 3
Las formas: vectorial, paramétrica y simétrica son
usadas para representar una recta en el espacio
3D.
v es el vector dirección paralelo a la recta , donde
v=tP0P; tR

y
z
x
v= a; b; c PO(xo; yo; zo)
P(x; y; z)
OP0
O
OP
OP=<x; y; z>
OP0=<x0; y0; z0>
Sean:

Ecuaciones de una recta en el espacio

4. 4
Ecuaciones de una recta en el espacio
Si es una recta que pasa por el punto Po(xo; yo; zo)
y en la dirección del vector no nulo v = a; b; c,
entonces un punto P(x; y; z) está en sí y sólo si


a, b y c son diferentes de cero
Vectorial:
Paramétrica:
c
zz
b
yy
a
xx 000 




Simétrica:
Rt
ctzz
btyy
atxx









;
0
0
0
OP = OP0 + tv, tR

5. 5
a) Determine las ecuaciones paramétricas y
simétrica de la recta que pasa por los puntos
A(2; 4; -3) y B(3; -1; 1).
b) ¿En qué punto interseca esta recta al plano
xy?
Determinación de la ecuación de la recta:
1. Si se conoce dos puntos de la recta.

y
x
z
A=(2; 4; -3)
B=(3; -1; 1)

6. 6
2. Dado un punto de la recta y un vector director.
a) Determine una ecuación vectorial y las
ecuaciones paramétricas de la recta que pasa
por el punto (5; 1; 3) y que es paralela al
vector i+4j-2k.
b) Determine otros dos puntos sobre la recta.

v=i+4j-2k
y
x
z
P0=(5; 1; 3)
Determinación de la ecuación de la recta:

7. 7
3. Dado un punto y una recta paralela.
Determine las ecuaciones paramétricas y simétrica
de la recta que pasa por el punto A(1; -1; 1) y
paralela a la recta con ecuaciones: x+2 = y/2 = z–3.
x+2 = y/2 = z–3

y
x
z
P0=(1; -1; 1)

Determinación de la ecuación de la recta:

8. 8
Planos en el espacio
Para describir un plano en el espacio no basta
hacerlo mediante la ubicación de un vector
paralelo al plano.
y
x
z
P(x; y; z)
n
P0(x0; y0; z0)
y
x
z
v
P0(x0; y0; z0)
Sin embargo un vector perpendicular o “normal”
n al plano especifica por completo su dirección.

9. 9
Planos en el espacio
y
x
z
P(x; y; z)
P0(x0; y0; z0)
      0000
 zzcyybxxa
Dado un plano, se cumple que el producto escalar
del vector normal n y el vector P0P debe ser
cero.
n=a; b; c
0 000 ;;;; zzyyxxcba
0 PPn 0

10. 10
Vectorial:
General: 0 dczbyax
Las ecuaciones de un plano son:
Planos en el espacio
P0 : Punto conocido (xo; yo; zo)
P : Punto genérico (x; y; z)
n : Vector normal <a; b; c>
Los coeficientes de x, y, z, son las
componentes del vector normal <a; b; c>
0 PPn 0

11. 11
Ejemplos
1. Determine una ecuación del plano que pasa
por el punto P(2; 4; -1) con un vector normal
n = 2; 3; 4
2. Halle la ecuación del plano determinado por
los tres puntos A(2; 1; –1), B(–2; 0; 3) y
C(1; 4; 0).

12. 12
Producto vectorial
Dado los vectores
El producto cruz o vectorial u  v es:
u v1 2 3 1 2 3; ; ; ;u u u y v v v 
i j k
u v 1 2 3
1 2 3
u u u
v v v
 
u v i j k2 3 3 2 1 3 3 1 1 2 2 1( ) ( ) ( )u v u v u v u v u v u v      
Para ayudarnos a recordar la fórmula, usaremos la
notación de determinante:
Ejemplo
Si u = 4; -1; 2 y v = 1; -3; 2, halle u  v.

13. 13
Propiedades del producto vectorial
Si u, v y w son vectores y c es un número real,
se cumple que:
u  v = – (v  u)
u  (v + w) = u  v + u  w
(v + w)  u = v  u + w  u
c(u  v) = (cu)  v = u  (cv)
0  u = u  0 = 0
u  u= 0

14. 14
Propiedades del producto vectorial
j  k = i
i  j = k
k  i = j
Respecto a los vectores unitarios i, j, k se
tiene que:
x
y
z
i
j
k

15. 15
Características del producto vectorial
El producto u  v es ortogonal a u y v.
0v)vu(
0u)vu(


u  v

u
v
Si  es el ángulo entre u y v (0     ), entonces:
|u  v| = |u||v| sen

senvh
u
v
área= b x h = |u||v|sen = |u  v|
b

16. 16
Los alumnos deben revisar los ejercicios del libro
Cálculo de Varias Variables
de Stewart.
Ejercicios: 2, 4, 14, 22, 28,
34 y 38 de las páginas 792 y
793, así como 24, 26, 28, 30,
32 y 34 de las páginas 802 y
803.
Bibliografía

17. 1717
ClassPad
combine: Propiedad distributiva.

18. 1818
ClassPad
Para hallar la ecuación del plano determinado por
los tres puntos A(9; 5; 4), B(2; 8; 5) y C(7; 2; 6).
Paso 3: u  v
Vector normal al
plano
Ecuación
del plano

19. 1919
ClassPad
dotP: Realiza producto escalar.
u.v

20. 202020
ClassPad
crossP: Realiza producto vectorial.
u  v