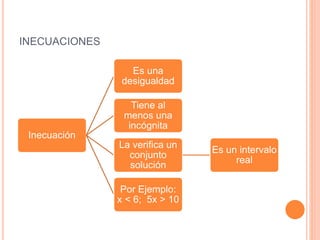
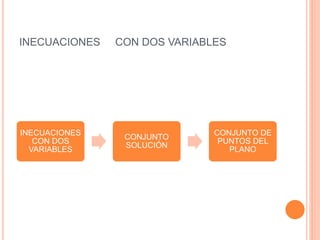
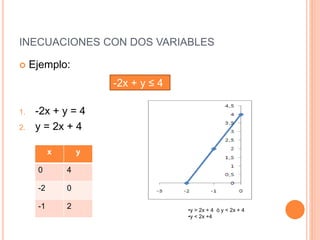
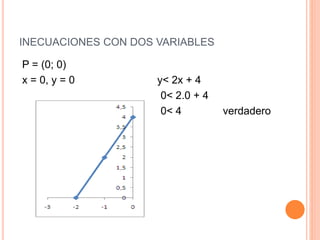
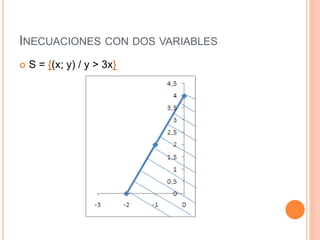
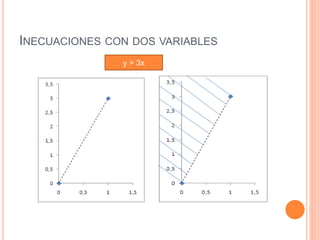
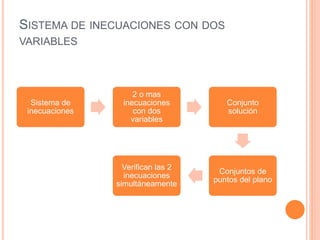
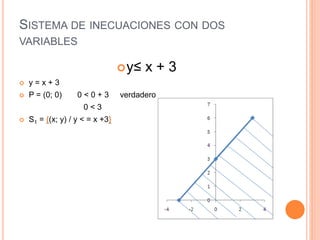
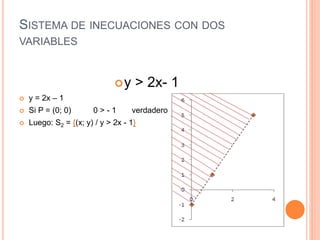
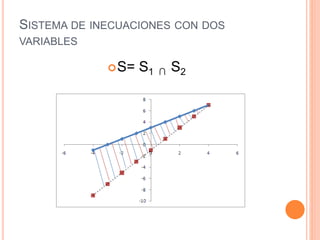
Este documento trata sobre inecuaciones lineales de una y dos variables y sistemas de inecuaciones de dos variables. Explica qué es una inecuación, sus propiedades y cómo verificar si un punto pertenece al conjunto solución de una inecuación. Luego, introduce las inecuaciones con dos variables y los sistemas de inecuaciones con dos variables, definiendo qué es un sistema de inecuaciones y cómo encontrar el conjunto solución como la intersección de los conjuntos solución de cada inecuación.

1. INECUACIONES LIENALES EN UNA
Y DOS VARIABLES. SISTEMAS DE
INECUACIONES EN DOS
VARIABLES.
INTEGRANTES: Beltrán Paula- Casares Carina- Chelela
Anahí- Sosa Abril- Tonda Rocío
CURSO: 3º2ª economía
MATERIA: Matemática
PROFESORA: Juliana Isola

2. INECUACIONES
Inecuación
Es una
desigualdad
Tiene al
menos una
incógnita
La verifica un
conjunto
solución
Es un intervalo
real
Por Ejemplo:
x < 6; 5x > 10

3. INECUACIONES
 Propiedades:
 x+6>4
x+6-6>4-6
x>-2
 8x+5<21
8x<16
x<16:8
x<2
-9x -3 ≤15
-9x ≤ 18
x ≥18 : (-9)
x ≥ -2

4. INECUACIONES CON DOS VARIABLES
INECUACIONES
CON DOS
VARIABLES
CONJUNTO
SOLUCIÓN
CONJUNTO DE
PUNTOS DEL
PLANO

5. INECUACIONES CON DOS VARIABLES
 Ejemplo:
1. -2x + y = 4
2. y = 2x + 4
-2x + y ≤ 4
x y
0 4
-2 0
-1 2 •y > 2x + 4 ò y < 2x + 4
•y < 2x +4

6. INECUACIONES CON DOS VARIABLES
P = (0; 0)
x = 0, y = 0 y< 2x + 4
0< 2.0 + 4
0< 4 verdadero

7. INECUACIONES CON DOS VARIABLES
 S = {(x; y) / y > 3x}

8. INECUACIONES CON DOS VARIABLES
y > 3x

9. SISTEMA DE INECUACIONES CON DOS
VARIABLES
Sistema de
inecuaciones
2 o mas
inecuaciones
con dos
variables
Conjunto
solución
Conjuntos de
puntos del plano
Verifican las 2
inecuaciones
simultáneamente

10. SISTEMA DE INECUACIONES CON DOS
VARIABLES
y ≤ x + 3 (1) =s1
y > 2x- 1 (2) =s2
S = S1 ∩ S2 es el conjunto solución del sistema

11. SISTEMA DE INECUACIONES CON DOS
VARIABLES
y≤ x + 3
 y = x + 3
 P = (0; 0) 0 < 0 + 3 verdadero
0 < 3
 S1 = {(x; y) / y < = x +3}

12. SISTEMA DE INECUACIONES CON DOS
VARIABLES
y > 2x- 1
 y = 2x – 1
 Si P = (0; 0) 0 > - 1 verdadero
 Luego: S2 = {(x; y) / y > 2x - 1}

13. SISTEMA DE INECUACIONES CON DOS
VARIABLES
S= S1 ∩ S2