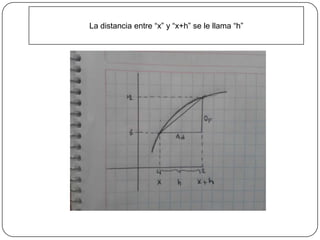
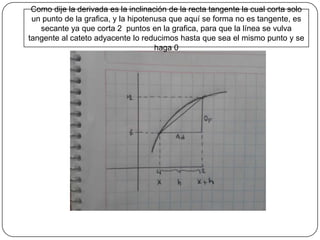
La derivada es la pendiente de la línea tangente a una curva en un punto. Se calcula como el límite de la razón entre los cambios en las funciones dividido por los cambios en la variable independiente a medida que este tiende a cero. Existen cuatro pasos para derivar una función: 1) determinar la función con un cambio en la variable, 2) sustituir en la fórmula de derivada, 3) simplificar, y 4) aplicar el límite. Las fórmulas de derivación dependen de si la función contiene una variable, una variable con potencia, o

1. LA DERIVADA

2. ¿Qué es?
 La derivada no es mas que la pendiente de una
recta cualquiera la cual es tangente a una cuerva
continua en “a” y en “b” si no es continua no es
posible econtrar la derivada

3. Primero veremos la derivada por medio de la grafica.
En la línea curva existen 2 puntos que son los que están marcados con
amarillo que son el resultado de las líneas de f(x+h) que es el 12 con x+h
que es el 12, y el otro es el de f(x) que es el 6 con x que es el 4

4. La distancia entre “x” y “x+h” se le llama “h”

5. Uniendo los 2 puntos se formara un triangulo rectángulo y estos los lados de
este el que esta abajo se le llama “cateto adyacente” y al que esta al lado
derecho se le llama “ cateto opuesto”

6. Ahora tenemos que encontrar la tangente del ángulo que se forma, para saber
el valor del cateto adyacente a “x+h” le restamos “x” y como no damos cuenta
es el valor de “h” y para el cateto opuesto a f(x+h) le restamos f(x). En este
caso el cateto Op=4 y el cateto Ad=8

7. Como dije la derivada es la inclinación de la recta tangente la cual corta solo
un punto de la grafica, y la hipotenusa que aquí se forma no es tangente, es
secante ya que corta 2 puntos en la grafica, para que la línea se vulva
tangente al cateto adyacente lo reducimos hasta que sea el mismo punto y se
haga 0

8. Para encontrar la tangente del ángulo lo aremos sacado un
pequeña formula para que sea mas fácil y al final queda una
formula como la que esta en el recuadro rojo
Sustituimos el cateto
opuesto por “f(x+h) –
f(x)” Y al cateto adyacente por
“x+h+x” pero como
existen 2 “x” las
eliminamos
Y al final es esta la
formula que nos
queda

9. Ahora explicare la regla general de derivación
por el método de 4 pasos
REGLA GENERAL DE DERIVACIÓN
ESTOS SON LOS PASOS CUATRO A
SEGUIR
1.Determinar f(x+h)
2.Sustituir en la formula
3.Simplificar
4.Ampliar el limite

10. Para mostrar como se utilizan estos cuatro
pasos, pondré un ejemplo:
DERIVAR: sustituimos la “x” por “(x+h)”
SUSTITUIR: sustituimos la primera parte por “f´(x)” y después del
= agregamos lim h-0 ponemos la primara parte de la función
anterior y agregamos la función a derivar, y todo eso sobre “h”

11. SIMPLIFICAR: multiplicamos el 6 por lo valores que están
adentro del paréntesis y al cuadrado y eso lo ponemos entre
paréntesis afuera del paréntesis ponemos la función a derivar
con signo negativo. Todo esto sobre “h”
Seguimos en el paso 3 en este volvemos a multiplicar el valor de
afuera por los valores de adentro y como se repite “seis exis al
cuadrado” los eliminamos, y como tambien se repite “h” pues a
12 le quitamos una y a 6x2 le quitamos a la potencia uno y solo
nos quedara 6x. Todo esto sobre “h”

12. Nos quedara esto y seguimos simplificando así que
eliminamos las “h” que están afuera
APLICAR EL LIMITE: ahora aplicamos el limite y queda como se
muestra en la imagen y como “h” vale 0 pues multiplicamos 6x0 y
nos da 0 entonces el resultado final es 12x

13. Ahora voy a mostrar las formulas de la derivación para así
no hacer un proceso completo solo con los valores que ya
tienes sacar el resultado final
Cuando no tiene “x” el resultado siempre
sera 0
Cuando solo tiene una “x” sin numero siempre
será 1

14. Cuando tiene numero mas “x” sin potencia el
resultado siempre será el puro numero que este con la
“x”
Cuando es “x” mas potencia, multiplica la potencia por
“x” y a la potencia réstale uno y ese será el resultado

15. Cuando sea numero mas “x” mas potencia, multiplica el
numero por la potencia y a la potencia de “x” réstale uno y ese
será el resultado