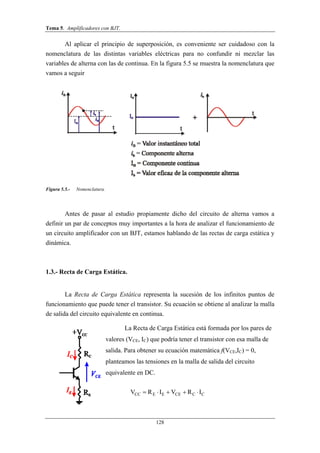
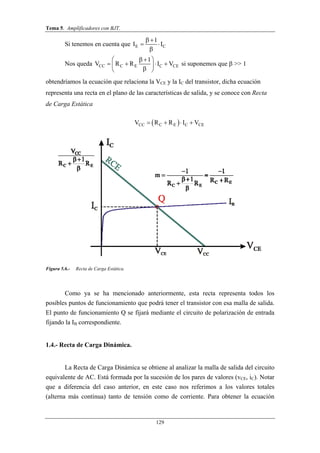
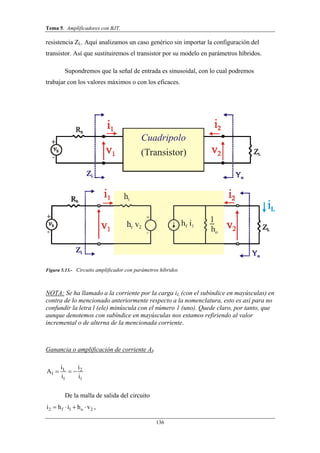
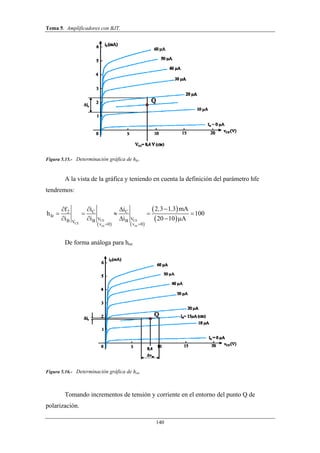
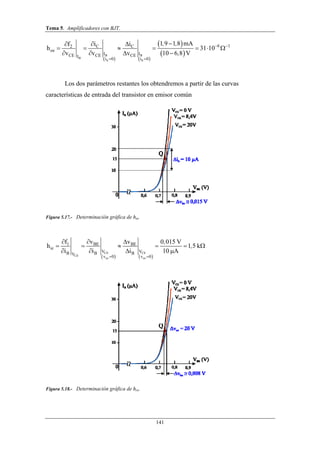
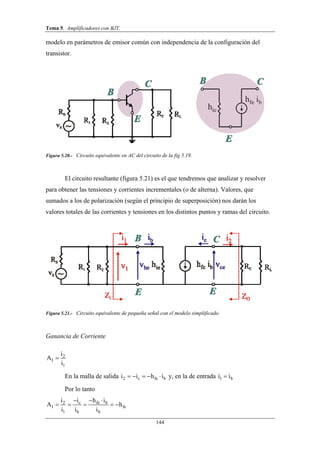
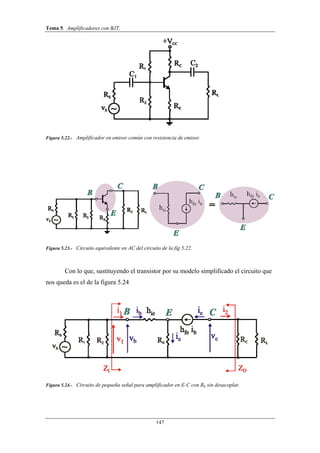
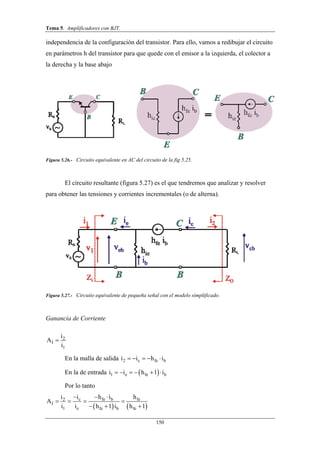
Este documento trata sobre amplificadores con transistores BJT. Explica el principio de superposición para analizar estos circuitos, dividiéndolos en componentes de continua y alterna. También introduce las rectas de carga estática y dinámica, que representan los puntos de funcionamiento del transistor. Finalmente, describe el modelo de pequeña señal del BJT usando parámetros híbridos.