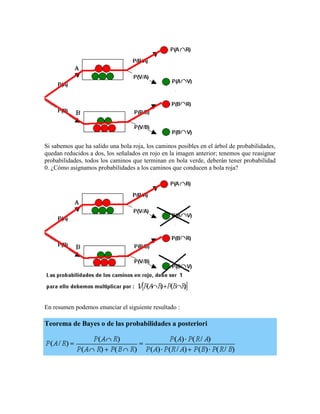
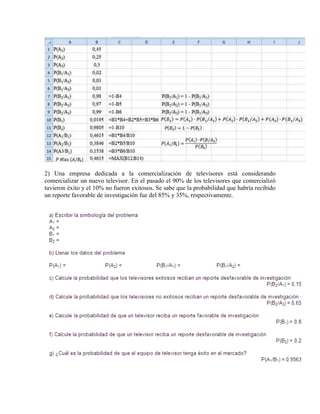
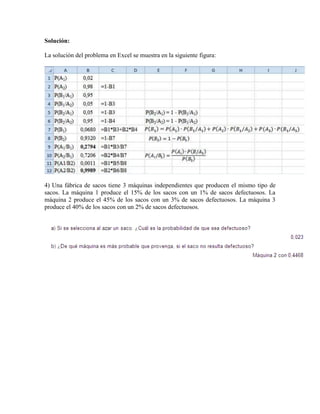
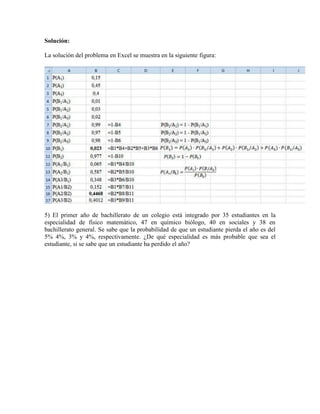
Este documento introduce los conceptos básicos de la teoría de probabilidad, incluyendo el teorema de la probabilidad total, el teorema de Bayes y las definiciones de probabilidad clásica, frecuentista, subjetiva y axiomática. Explica estos teoremas y definiciones a través de ejemplos como lanzar una moneda o predecir el tiempo, y destaca la importancia de asignar valores numéricos a las probabilidades para poder analizarlos matemáticamente.

1. Introducción a la teoría de la probabilidad
Hay algunos resultados importantes del cálculo de probabilidades que son conocidos bajo los
nombres de teorema de la probabilidad compuesta, teorema de la probabilidad total y teorema de
Bayes. Veamos cuales son estos teoremas, pero previamente vamos a enunciar a modo de
recopilación, una serie de resultados elementales cuya demostración se deja como ejercicio para
el lector (algunos ya han sido demostrados anteriormente):
Laplace, eminente matemático francés de la última mitad del siglo XVIII y principios del
XIX, describía la teoría de la probabilidad como “el sentido común reducido al cálculo”.
Veamos como la siguiente anécdota justifica esta descripción.
Dos estudiantes de Instituto intentan ponerse de acuerdo en como pasar una tarde.
Acuerdan que tomarán su decisión lanzando una moneda. Si sale cara irán al cine, si sale
cruz saldrán a tomar una coca-cola y si la moneda cae de canto, estudiarán.
La historia no es tan trivial como pueda parecer, con ella podemos aprender mucho. El
sentido común, basando su juicio en la experiencia, nos indica que los estudiantes quieren
saltarse la necesidad de estudiar. En otras palabras sabemos intuitivamente que la moneda
no caerá de canto, que lo hará sobre la cara o sobre la cruz. Más aún, si la moneda es legal,
tenemos la certeza moral de que las posibilidades de que salga cara o cruz son las mismas.
Pues bien la teoría de la probabilidad se basa en la asunción que hacemos de cuestiones
tales como estas : ¿Cuál es la probabilidad de que una moneda caiga sobre el borde? ¿Cuál
es la probabilidad de que salga cara? ¿Cuál es la probabilidad de que salga cruz?
Para poder tratar estas cuestiones desde un punto de vista matemático, es necesario asignar
valores numéricos a cada una de la probabilidades involucradas.
Supongamos por el momento que denotamos por p el valor numérico de la probabilidad de
que al lanzar una moneda, salga cara. Puesto que es igualmente posible que al lanzar la
moneda, salga cruz, la probabilidad de que salga cruz también debe tener asignado el valor
p.
Como tenemos la certeza de que saldrá cara o cruz sigue que 2p debe ser el valor asignado
al suceso seguro, el que ocurrirá siempre que lancemos una moneda al aire. Podemos elegir
cualquier valor que nos plazca para el suceso seguro. Es costumbre elegir el valor 1. Esto
es: asumimos que 2p=1. Entonces la probabilidad de que la moneda muestre cara es : 1/2 ;
la probabilidad de que muestre cruz es : 1/2; y la probabilidad de que salga cara o cruz es:
Si analizamos detalladamente el ejemplo, podemos apreciar :
Un experimento aleatorio, lanzar una moneda al aire

2. Unos resultados puntuales, sale cara o sale cruz y no podemos tener la certeza de antemano
de que sea cara o sea cruz.
Unas asignaciones de probabilidad a cada uno de los resultados, que se basan en el sentido
común y en nuestra experiencia previa.
Vamos a definir de manera más precisa cada uno de los elementos que intervienen:
Observación:
Un resultado concreto de un experimento es un elemento del espacio muestral asociado al
experimento, conceptualmente suceso y resultado son dos cosas distintas. Los resultados de
un experimento aleatorio se suelen representar con letras minúsculas, los sucesos con letras
mayúsculas.
En el ejemplo anterior, el suceso A ocurre siempre que el resultado del experimento sea el
elemento 2, el elemento 4 o el elemento 6.
La confusión entre suceso y resultado se debe a que cuando el suceso es : " que al lanzar un
dado salga 2" y el resultado :"sale un dos al lanzar el dado", sólo ocurre el suceso cuando el
resultado es 2.
Suceso : "Sale un dos" es el subconjunto {2} del espacio muestral
Resultado : "Sale un dos" es el elemento 2 del espacio muestral

3. Funciones de distribución
El paso siguiente es asignar (distribuir) probabilidades. Las definiciones que siguen están
motivadas por el ejemplo del lanzamiento de una moneda, recordamos que en ese ejemplo a
cada resultado del espacio muestral le asignabamos un número no negativo tal que la suma
de todos los números asignados a cada resultado deberá ser 1.
Definición
Sea X una variable que representa a los posibles resultados de un experimento aleatorio, en
principio vamos a asumir que este experimento tiene sólo un número finito de posibles
resultados. Sea E, el espacio muestral del experimento. Una función de distribución para X
es una función real f cuyo dominio es E y que satisface:
El Teorema de la probabilidad total nos permite calcular la probabilidad de un suceso a
partir de probabilidades condicionadas:
Ejemplo: supongamos que si llueve la probabilidad de que ocurra un accidentes es x% y si
hace buen tiempo dicha probabilidad es y%. Este teorema nos permite deducir cuál es la
probabilidad de que ocurra un accidente si conocemos la probabilidad de que llueva y la
probabilidad de que haga buen tiempo.
La fórmula para calcular esta probabilidad es:
Es decir, la probabilidad de que ocurra el suceso B (en nuestro ejemplo, que ocurra un
accidente) es igual a la suma de multiplicar cada una de las probabilidades
condicionadas de este suceso con los diferentes sucesos A (probabilidad de un accidente
cuando llueve y cuando hace buen tiempo) por la probabilidad de cada suceso A.

4. Para que este teorema se pueda aplicar hace falta cumplir un requisito:
Los sucesos A tienen que formar un sistema completo, es decir, que contemplen todas
las posibilidades (la suma de sus probabilidades debe ser el 100%).
Ejemplo: al tirar una moneda, el suceso "salir cara" y el suceso "salir cruz" forman un
sistema completo, no hay más alternativas: la suma de sus probabilidades es el 100%
Ejemplo: al tirar un dado, que salga el 1, el 2, el 3, o el 4 no forman un sistema completo,
ya que no contempla todas las opciones (podría salir el 5 o el 6). En este caso no se podría
aplicar el teorema de la probabilidad total.
El Teorema de Bayes viene a seguir el proceso inverso al que hemos visto en el Teorema
de la probabilidad total:
Teorema de la probabilidad total: a partir de las probabilidades del suceso A
(probabilidad de que llueva o de que haga buen tiempo) deducimos la probabilidad del
suceso B (que ocurra un accidente).
Teorema de Bayes: a partir de que ha ocurrido el suceso B (ha ocurrido un accidente)
deducimos las probabilidades del suceso A (¿estaba lloviendo o hacía buen tiempo?).
La fórmula del Teorema de Bayes es:
Tratar de explicar estar fórmula con palabras es un galimatías, así que vamos a intentar
explicarla con un ejemplo. De todos modos, antes de entrar en el ejercicio, recordar que
este teorema también exige que el suceso A forme un sistema completo.
Ejercicio 1º: El parte meteorológico ha anunciado tres posibilidades para el fin de semana:
a) Que llueva: probabilidad del 50%.
b) Que nieve: probabilidad del 30%
c) Que haya niebla: probabilidad del 20%.
Según estos posibles estados meteorológicos, la posibilidad de que ocurra un accidente es la
siguiente:

5. a) Si llueve: probabilidad de accidente del 10%.
b) Si nieva: probabilidad de accidente del 20%
c) Si hay niebla: probabilidad de accidente del 5%.
Resulta que efectivamente ocurre un accidente y como no estábamos en la ciudad no
sabemos qué tiempo hizo (nevó, llovío o hubo niebla). El teorema de Bayes nos permite
calcular estas probabilidades:
Las probabilidades que manejamos antes de conocer que ha ocurrido un accidente se
denominan "probabilidades a priori" (lluvia con el 60%, nieve con el 30% y niebla con el
10%).
Una vez que incorporamos lainformación de que ha ocurrido un accidente, las
probabilidades del suceso A cambian: son probabilidades condicionadas P (A/B), que se
denominan "probabilidades a posteriori".
Vamos a aplicar la fórmula:
a) Probabilidad de que estuviera lloviendo:
La probabilidad de que efectivamente estuviera lloviendo el día del accidente (probabilidad
a posteriori) es del 71,4%.
b) Probabilidad de que estuviera nevando:
La probabilidad de que estuviera nevando es del 21,4%.
c) Probabilidad de que hubiera niebla:

6. La probabilidad de que hubiera niebla es del 7,1%.
Ejemplo:
Sean tres equipos de futbol, a, b y c que se presentan a un torneo de verano, sólo uno
ganará el torneo. El espacio muestral es el conjunto de tres elementos, E={a,b,c}, donde
cada elemento corresponde al triunfo de cada uno de los equipos. Suponemos que a y b
tienen las mismas posibilidades de ganar y c tiene solamente la mitad de las posibilidades
de ganar que a. Debemos asignar probabilidades de modo que :
Sea el suceso A, "gana el trofeo el equipo a" ; el suceso B, "gana el trofeo el equipo b" y el
suceso C, "gana el trofeo el equipo c". En el lenguaje de la teoría de conjuntos:

7. En este último caso se puede apreciar como un suceso se puede describir en términos de
otros sucesos utilizando las construcciones standard de la teoría de conjuntos.
Las representaciones gráficas de las construcciones de la teoría de conjuntos se llaman
diagramas de Venn. En ocasiones es muy conveniente para resolver un problema de
probabilidad hacer la representación gráfica del espacio muestral y de los sucesos
(subconjuntos del espacio muestral) que intervienen en el problema.

8. Probabilidad condicionada
Esta definición clásica de probabilidad fue una de las primeras que se dieron
(1900) y se atribuye a Laplace; también se conoce con el nombre de probabilidad
a priori pues, para calcularla, es necesario conocer, antes de realizar el
experimento aleatorio, el espacio muestral y el número de resultados o sucesos
elementales que entran a formar parte del suceso
La aplicación de la definición clásica de probabilidad puede presentar dificultades
de aplicación cuando el espacio muestral es infinito o cuando los posibles
resultados de un experimento no son equiprobables. Ej: En un proceso de
fabricación de piezas puede haber algunas defectuosas y si queremos determinar
la probabilidad de que una pieza sea defectuosa no podemos utilizar la definición
clásica pues necesitaríamos conocer previamente el resultado del proceso de
fabricación
Para resolver estos casos, se hace una extensión de la definición de probabilidad,
de manera que se pueda aplicar con menos restricciones, llegando así a la
definición frecuentista de probabilidad
3. Definición Frecuentista de la Probabilidad
La definición frecuentista consiste en definir la probabilidad como el límite cuando
n tiende a infinito de la proporción o frecuencia relativa del suceso.
Sea un experimento aleatorio cuyo espacio muestral es E Sea A cualquier suceso
perteneciente a E Si repetimos n veces el experimento en las mismas
Condiciones, la frecuencia relativa del suceso A será:
Cuando el número n de repeticiones se hace muy grande la frecuencia relativa
converge hacia un valor que llamaremos probabilidad del suceso A.
Es imposible llegar a este límite, ya que no podemos repetir el experimento un
número infinito de veces, pero si podemos repetirlo muchas veces y observar
como las frecuencias relativas tienden a estabilizarse
Esta definición frecuentista de la probabilidad se llama también probabilidad a
posteriori ya que sólo podemos dar la probabilidad de un suceso después de
repetir y observar un gran número de veces el experimento aleatorio
correspondiente. Algunos autores las llaman probabilidades teóricas

9. 4. Definición Subjetiva de la Probabilidad
Tanto la definición clásica como la frecuentista se basan en las repeticiones del
experimento aleatorio; pero existen muchos experimentos que no se pueden
repetir bajo las mismas condiciones y por tanto no puede aplicarse la
interpretación objetiva de la probabilidad
En esos casos es necesario acudir a un punto de vista alternativo, que no
dependa de las repeticiones, sino que considere la probabilidad como un concepto
subjetivo que exprese el grado de creencia o confianza individual sobre la
posibilidad de que el suceso ocurra
Se trata por tanto de un juicio personal o individual y es posible por tanto que,
diferentes observadores tengan distintos grados de creencia sobre los posibles
resultados, igualmente válidos
5. Definición Axiomática de la Probabilidad
La definición axiomática de la probabilidad es quizás la más simple de todas las
definiciones y la menos controvertida ya que está basada en un conjunto de
axiomas que establecen los requisitos mínimos para dar una definición de
probabilidad. La ventaja de esta definición es que permite un desarrollo riguroso y
matemático de la probabilidad. Fue introducida por A. N. Kolmogorov y aceptada
por estadísticos y matemáticos en general
Así el suceso : "Seat Toledo de color rojo" lo representamos por : T ∩ R y la probabilidad
de este suceso, sigue de la tabla :
Rojo Azul Totales
SeatPanda 2 8 10
SeatToledo 7 3 10
Totales 9 11 20
P( T ∩ R ) = 7/20
La probabilidad de que el coche sea un Seat Toledo es :
Rojo Azul Totales

10. SeatPanda 2 8 10
SeatToledo 7 3 10
Totales 9 11 20
P(T)=10/20 = 1/2
¿Qué ocurre si, una vez que el concursante ha elegido puerta, el presentador, le da la pista
de que el coche que hay tras la puerta es rojo?. Tendremos que cambiar la probabilidad al
suceso T y al suceso P. A la probabilidad del suceso T cuando se sabe que ha ocurrido R, le
llamamos probabilidad condicionada de T, sabiendo que ha ocurrido R y escribimos:
P(T/R)
Para asignar las nuevas probabilidades hemos de ser consecuentes con las propiedades que
debe cumplir toda asignación de probabilidades. El nuevo espacio muestral es el señalado
en rojo en la tabla siguiente. Por tanto asignamos así las probabilidades:
Rojo Azul Totales
SeatPanda 2 8 10
SeatToledo 7 3 10
Totales 9 11 20
P(T/R) = 7/9 ; P(P/R) = 2/9
De la tabla anterior, siguen fácilmente las siguientes relaciones :
Consideremos ahora el siguiente experimento : Dos urnas, A y B ,la urna A, contiene 3
bolas verdes y 2 bolas rojas, la urna B contiene 2 bolas verdes y 3 bolas rojas.
Se realiza el experimento en dos tiempos, primero se selecciona urna por un procedimiento
aleatorio y posteriormente de la urna elegida se extrae una bola.
Para representar, de forma muy adecuada, este tipo de experimentos, se realiza un esquema,
llamado : árbol de probabilidades

11. Cada flecha del diagrama se denomina rama del árbol; a cada rama, asignamos la
probabilidad que le corresponde. Un recorrido, desde el comienzo del experimento hasta el
final, se llama un camino.
Si sabemos que ha ocurrido el suceso A, tenemos que volver a asignar probabilidades a los
distintos caminos; todos los caminos que comienzan por el suceso B, tendrán probabilidad 0
y los que empiezan por el suceso A :
Hay que aceptar por tanto las mismas relaciones entre probabilidades a las que habíamos
llegado en el experimento anterior :

12. Para concretar tenemos que admitir la siguiente definición:
Definición 1. Probabilidad condicionada
De un suceso R sabiendo que ha ocurrido otro A
Y dos teoremas:
Teorema 1. Regla del producto
De la definicion 1, despejando, sigue que:
Teorema 2. Probabilidad total
Si A y B forman un sistema completo de sucesos , la probabilidad de cualquier otro suceso
R es:
Sucesos dependientes
Dos sucesos son dependientes si el resultado de uno influye en el otro. Los sucesos A y B
son dependientes si y sólo si P(A) es distinto de P(A/B) y P(B) es distinto de P(B/A)
Sucesos independientes
Dos sucesos son independientes si el resultado de uno no influye en el resultado del otro.
Los sucesos A y B son independientes si y sólo si P(A)=P(A/B) y P(B)=P(B/A).

13. Teorema de Bayes
La interpretación más aceptada del teorema de Bayes, es que su estructura permite el
calculo de probabilidades después de haber sido realizado un experimento (probabilidades
aposteriori), basándose en el conocimiento de la ocurrencia de ciertos eventos que
dependan del evento estudiado, o sea, se parte de probabilidades conocidas antes de
efectuar el experimento (probabilidades apriori), las cuales son afectadas por las
probabilidades propias del experimento (las que aparecen durante la ocurrencia del evento).
Continuando nuestro análisis sobre el teorema de Bayes, la probabilidad condicional de Ai
dado B, para cualquier i, es:
Aplicando en el numerador la Regla de Multiplicación P(Ai B) = P(Ai) P(B|Ai) y en el
denominador el Teorema de Probabilidad Total P(B) = P(A1) P(B | A1) + P(A2) P(B | A2) +
. . . + P(An) P(B | An), obtenemos la ecuación que representa al:
Teorema de Bayes

14. Ejemplo 3. 11. Referente al problema de la fábrica que produce dos tipos de reguladores A
y B visto anteriormente en la aparte corresponde al Teorema de Probabilidad Total, cabe
hacer el siguiente análisis: si se selecciona un regulador al azar de la producción de la
fábrica y se ve que funciona bien ¿Cuál es la probabilidad de que sea del tipo B?
Solución
En este caso el estudio se restringe a los reguladores que funcionan bien, por lo que ese
evento actúa como espacio muestral reducido, o sea como evento condición. Por lo tanto, el
planteamiento de la pregunta es P(B | F).
Los datos que se tienen son :
P(A) = 0.75 P(F | A) = 0.95
P(B) = 0.25 P(F | B) = 0.98
De acuerdo al Teorema de Bayes:
Podemos observar que el denominador corresponde al resultado obtenido al aplicar el
Teorema de Probabilidad Total, lo cual debe ser así, ya que la probabilidad condicional
establece que . De esta forma podemos ver que la Probabilidad
Total es el denominador de la fórmula del Teorema de Bayes. También podemos observar
que aplicando los conceptos de la Regla de Multiplicación y del Teorema de Probabilidad
Total llegamos al planteamiento del teorema de Bayes, Veamos:

15. Ejemplo 3. 12. Una fábrica que produce material para la construcción tiene 3 máquinas, a
las que se les denomina A, B y C. La máquina A produce tabique, la B adoquín y la C
losetas. La máquina A produce el 50% de la producción total de la fábrica, la B el 30% y la
C el 20%. Los porcentajes de artículos defectuosos producidos por las máquinas son,
respectivamente, 3%, 4% y 5%. Si se selecciona un artículo al azar y se observa que es
defectuoso, encontrar la probabilidad de que sea un tabique.
Solución
Definamos el evento D como sea un artículo defectuoso. De acuerdo a esto tenemos
que:
P(A) = 0.5 P(D | A) = 0.03
P(B) = 0.3 P(D | B) = 0.04
P(C) = 0.2 P(D | C) = 0.05
Si el artículo del que deseamos calcular la probabilidad es un tabique, significa que
es producido por la máquina A. También observamos que en la solución solamente
participan los artículos defectuosos, ya que se pone por condición esta característica. Por lo
tanto:

16. Ejemplo 3. 13. A un congreso asisten 100 personas, de las cuales 65 son hombres y 35 son
mujeres. Se sabe que el 10% de los hombres y el 6% de las mujeres son especialistas en
computación. Si se selecciona al azar a un especialista en computación ¿Cuál es la
probabilidad de que sea mujer?
Solución
Definamos los eventos:
H: Sea un hombre
M: Sea una mujer
E: La persona sea especialista en computación
Tenemos que:
Por lo tanto:

17. Ejemplo
Se dispone de tres cajas con bombillas. La primera contiene 10 bombillas, de las cuales hay
cuatro fundidas; en la segunda hay seis bombillas, estando una de ellas fundida, y la tercera
caja hay tres bombillas fundidas de un total de ocho. ¿Cuál es la probabilidad de que al
tomar una bombilla al azar de una cualquiera de las cajas, esté fundida?

18. Si sabemos que ha salido una bola roja, los caminos posibles en el árbol de probabilidades,
quedan reducidos a dos, los señalados en rojo en la imagen anterior; tenemos que reasignar
probabilidades, todos los caminos que terminan en bola verde, deberán tener probabilidad
0. ¿Cómo asignamos probabilidades a los caminos que conducen a bola roja?
En resumen podemos enunciar el siguiente resultado :
Teorema de Bayes o de las probabilidades a posteriori

19. El teorema de Bayes se utiliza para revisar probabilidades previamente calculadas cuando
se posee nueva información. Desarrollado por el reverendo Thomas Bayes en el siglo XVII,
el teorema de Bayes es una extensión de lo que ha aprendido hasta ahora acerca de la
probabilidad condicional.
Comúnmente se inicia un análisis de probabilidades con una asignación inicial,
probabilidad a priori. Cuando se tiene alguna informaciónadicional se procede a calcular las
probabilidades revisadas o a posteriori. El teorema de Bayes permite calcular las
probabilidades a posteriori y es:
Ejemplos ilustrativos
1) Una compañía de transporte público tiene tres líneas en una ciudad, de forma que el 45%
de los autobuses cubre el servicio de la línea 1, el 25% cubre la línea 2 y el 30% cubre el
servicio de la línea 3. Se sabe que la probabilidad de que, diariamente, un autobús se averíe
es del 2%, 3% y 1% respectivamente, para cada línea.
a) Calcular la probabilidad de que, en un día, un autobús sufra una avería
b) Calcular la probabilidad de que, en un día, un autobús no sufra una avería
c) ¿De qué línea de transporte es más probable que un autobús sufra una avería?

20. Solución:
a) Calcular la probabilidad de que, en un día, un autobús sufra una avería
Empleando la fórmula de probabilidad total se obtiene:
b) Calcular la probabilidad de que, en un día, un autobús no sufra una avería
Empleando la fórmula de probabilidad total se obtiene:
c) ¿De qué línea de transporte es más probable que un autobús sufra una avería?
Se debe calcular las tres probabilidades a posteriori empleando el Teorema de Bayes

21. La probabilidad de que sea de la línea 1, sabiendo que sufre una avería es:
La probabilidad de que sea de la línea 2, sabiendo que sufre una avería es:
La probabilidad de que sea de la línea 3, sabiendo que sufre una avería es:
Entonces, sabiendo que el autobús sufre una avería, lo más probable es que sea de la línea
1, ya que esta probabilidad
, es la mayor.
Los cálculos enExcel se muestran en la siguiente figura:

22. 2) Una empresa dedicada a la comercialización de televisores está considerando
comercializar un nuevo televisor. En el pasado el 90% de los televisores que comercializó
tuvieron éxito y el 10% no fueron exitosos. Se sabe que la probabilidad que habría recibido
un reporte favorable de investigación fue del 85% y 35%, respectivamente.

23. Solución:
a) Escribir la simbología del problema
A1 = Televisores exitosos
A2 = Televisores no exitosos
B1 = Reporte favorable de investigación
B2 = Reporte desfavorable de investigación
La solución del problema en Excel se muestra en la siguiente figura:
3) La probabilidad de que una persona tenga una determinada enfermedad es de 0,02.
Existen pruebas de diagnóstico médico disponibles para determinar si una persona tiene
realmente la enfermedad. Si la enfermedad realmente está presente, la probabilidad de que
la prueba de diagnóstico indique la presencia de la enfermedad es de 0,95.

24. Solución:
La solución del problema en Excel se muestra en la siguiente figura:
4) Una fábrica de sacos tiene 3 máquinas independientes que producen el mismo tipo de
sacos. La máquina 1 produce el 15% de los sacos con un 1% de sacos defectuosos. La
máquina 2 produce el 45% de los sacos con un 3% de sacos defectuosos. La máquina 3
produce el 40% de los sacos con un 2% de sacos defectuosos.

25. Solución:
La solución del problema en Excel se muestra en la siguiente figura:
5) El primer año de bachillerato de un colegio está integrado por 35 estudiantes en la
especialidad de físico matemático, 47 en químico biólogo, 40 en sociales y 38 en
bachillerato general. Se sabe que la probabilidad de que un estudiante pierda el año es del
5% 4%, 3% y 4%, respectivamente. ¿De qué especialidad es más probable que sea el
estudiante, si se sabe que un estudiante ha perdido el año?

26. Solución:
La solución del problema en Excel se muestra en la siguiente figura: