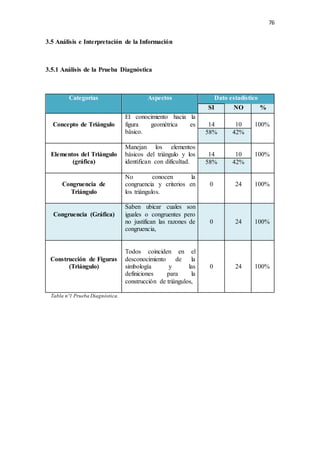
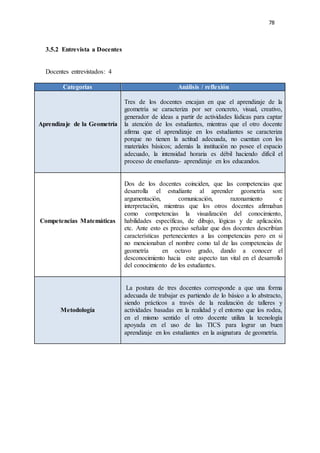
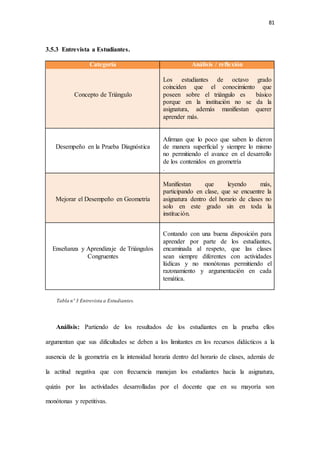
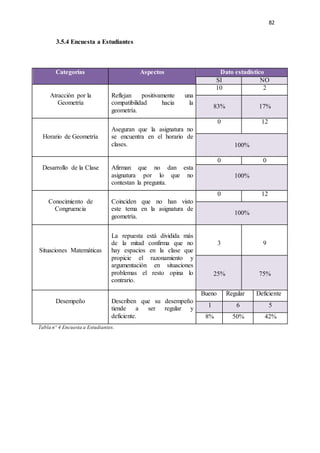
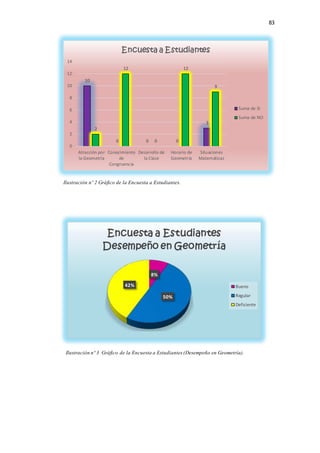
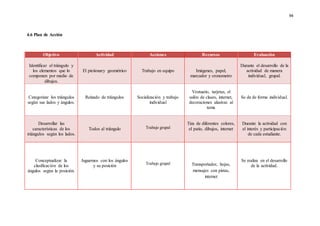
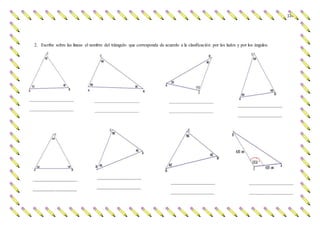
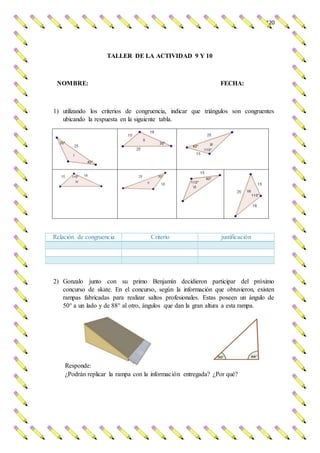
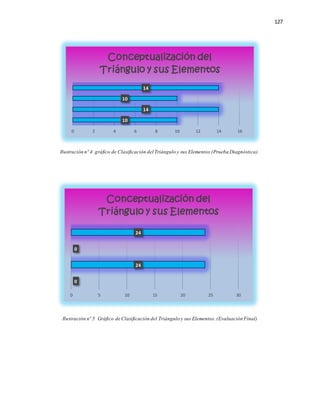
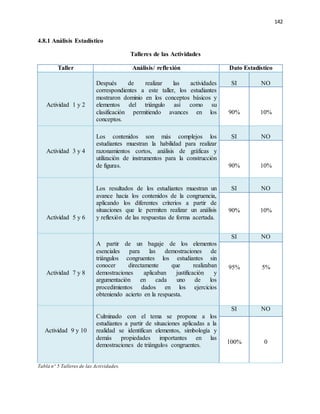
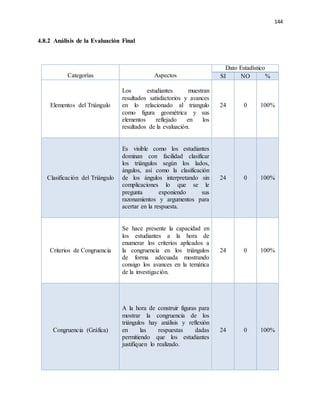
El documento presenta una investigación sobre el desarrollo de la competencia de razonamiento y argumentación matemática en estudiantes de octavo grado, en el contexto de triángulos congruentes. Se identifican dificultades comunes que presentan los estudiantes al realizar demostraciones, como confusión en datos conocidos, falta de claridad en el diseño y aplicación deficiente de conceptos. El trabajo propone diseñar e implementar una propuesta pedagógica basada en actividades concretas que permitan fortalecer estas competencias, a través del an