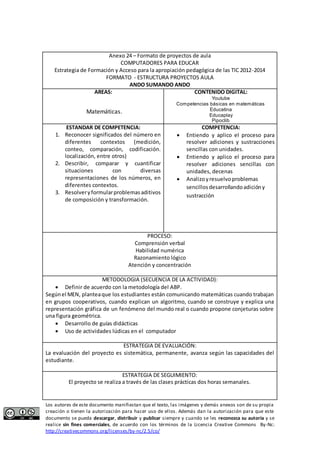
Este documento presenta un proyecto de aula para fortalecer las habilidades de suma en estudiantes de primer grado a través de estrategias lúdicas y el uso de las TIC. El proyecto busca mejorar los procesos de adición mediante la creación de guías y juegos, y evaluará el aprendizaje de los estudiantes basado en su interés y compromiso.