Este documento presenta conceptos preliminares sobre amplificadores operacionales. Explica la ley de Ohm y define cuadripolos elementales como convertidores o amplificadores de tensión, corriente, transresistencia o transconductancia. También discute los efectos de carga que ocurren cuando se mide la señal de salida de un circuito y cómo esto debe considerarse para analizar circuitos con realimentación.


![Diseño con Amplificadores Operacionales 3
Capítulo I: Conceptos Preliminares
I.1- Ley de Ohm
Suponemos al lector familiarizado con los conceptos de diferencia de
potencial o tensión eléctrica entre dos puntos de un circuito (voltios, V) y la
corriente eléctrica que produce (amperios, A) cuando entre esos dos puntos
existe algún medio conductor como puede ser una resistencia eléctrica. La
Ley de Ohm establece que la diferencia de potencial V entre los extremos
de una resistencia eléctrica R y la corriente I que circula de un extremo a
otro a través de esa resistencia, son directamente proporcionales. Una de las
formas que adopta la Ley de Ohm es:
V
R= (Ω ≡ V /A) (1)
I
forma ésta que permite definir la unidad de resistencia eléctrica, el Ohmio
(Ω) como el valor de aquella resistencia que cuando es atravesada por una
corriente de 1 A, presenta un voltaje entre sus extremos de exactamente 1
voltio. Como el tiempo de relajación dieléctrica [1] del material de la
resistencia (τd) suele ser inferior al picosegundo, podemos suponer que a
efectos prácticos, V e I aparecen simultáneamente en el circuito, siendo su
cociente el valor R. Una vez establecido lo anterior, no hay inconveniente
en suponer que uno es la causa de que aparezca el otro y esta forma de
pensar nos permite considerar unos cuadripolos elementales con una señal
de excitación a su entrada que hace aparecer instantáneamente una señal
respuesta a su salida.
I.2- Cuadripolos elementales
La forma de pensar que supone que la entrada se excita en corriente
(generador I) y que a consecuencia de ello se genera la tensión V entre los
extremos de la resistencia R (señal de salida), nos permite obtener la señal
respuesta a la salida mediante la Ley de Ohm, como el producto de una
función de transferencia del cuadripolo y de la señal excitación. Así
tenemos la expresión:
V (respuesta) = R (función de transferencia) × I (excitación) (2)
que corresponde a la visión circuital de un cuadripolo amplificador que se
presenta en la Figura 1.](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-3-2048.jpg)












![16
I.7- Generalización de la Ley de Ohm: Impedancias
Hemos ido viendo que una ley simple como la de Ohm, utilizada con
sentido común, nos da bastantes recursos para analizar circuitos (efectos de
carga, superposición, etc.). Sin embargo, el alcance de estos recursos sólo
se puede apreciar en su totalidad si se extienden a circuitos que además de
resistencias tengan otros componentes, y a señales de tensión y de corriente
que, en lugar de ser constantes en el tiempo, varíen de alguna forma a
medida que éste transcurre. Esos otros componentes lineales a los que nos
referimos son los condensadores (C) y las bobinas o inductancias (L). En
cuanto a la forma de variación temporal de las señales de tensión o de
corriente, la que estudiaremos es la variación senoidal o cosenoidal debido
a que cualquier otra forma de variación temporal de una magnitud física
(tensión, corriente, temperatura, etc) se puede “construir” como una suma
cuidadosa de señales senoidales y cosenoidales. Nos referimos a la síntesis
de Fourier de señales periódicas mediante sus armónicos, con la que
suponemos familiarizado al lector y si no es el caso, hay buenas referencias
sobre el tema [2] [3], que puede consultar. De esta forma, la respuesta de
un circuito a una señal excitación triangular periódica por ejemplo, será la
superposición de las respuestas a cada una de las señales senoidales que la
forman y esto no deja de ser una aplicación más de la superposición de
efectos de generadores que ya hemos recordado en este capítulo.
Aunque un estudio profundo nos llevaría a conceptos de autovalores,
autofunciones y aplicaciones entre espacios vectoriales, prescindiremos de
todo de ello y vamos a centrarnos en las señales senoidales y una de sus
interesantes propiedades que las hace únicas para su empleo en circuitos
Lineales e Invariantes en el Tiempo (LIT) como los que usaremos. Dicha
propiedad es que la señal respuesta de un circuito LIT a una señal senoidal
de excitación, también tiene la misma forma senoidal y, para fijar ideas,
podemos pensar que excitación y respuesta están relacionadas por una
función de transferencia como las expresiones (2) o (4). Por el contrario,
esto no sucederá en general con otras señales. Así por ejemplo, una señal
triangular aplicada a la entrada de un circuito LIT, no tiene por qué
conservar su forma cuando aparece a la salida, mientras que la senoidal
siempre lo hará. De ahí el interés de estas señales senoidales el tiempo.
Hasta ahora hemos considerado señales de tensión y de corriente que
eran constantes en el tiempo (de ahí su nombre con mayúsculas:V e I) y
como R también lo era, la relación entre la entrada y la salida del circuito
de la Figura 1 por ejemplo, era un simple número real que expresaba su
razón o cociente. Si en el circuito de la Figura 2 aplicamos una tensión
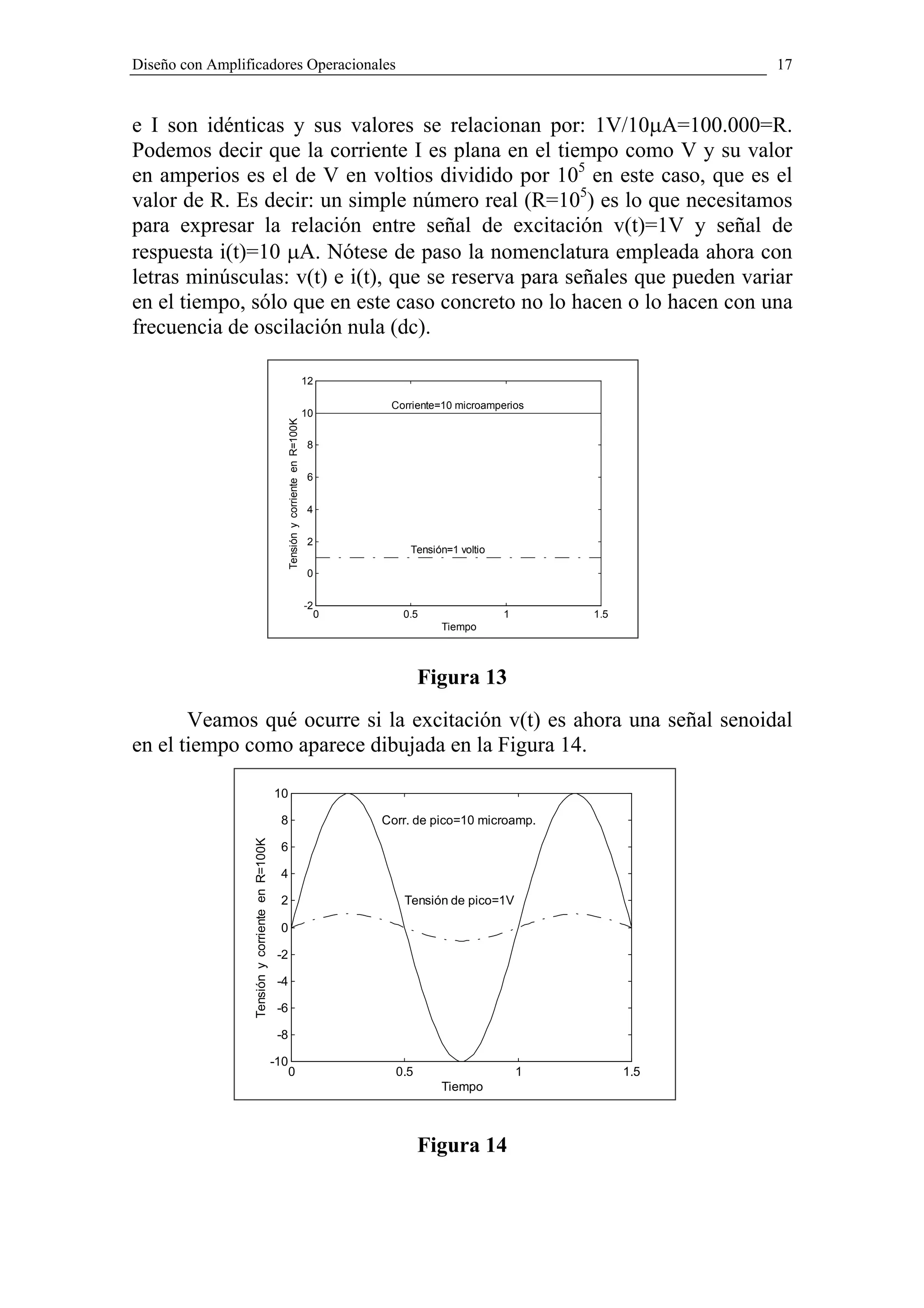
continua V=1V a una resistencia R=100 KΩ, la representación en el tiempo
de la tensión aplicada y de la corriente I que circula por la resistencia es la
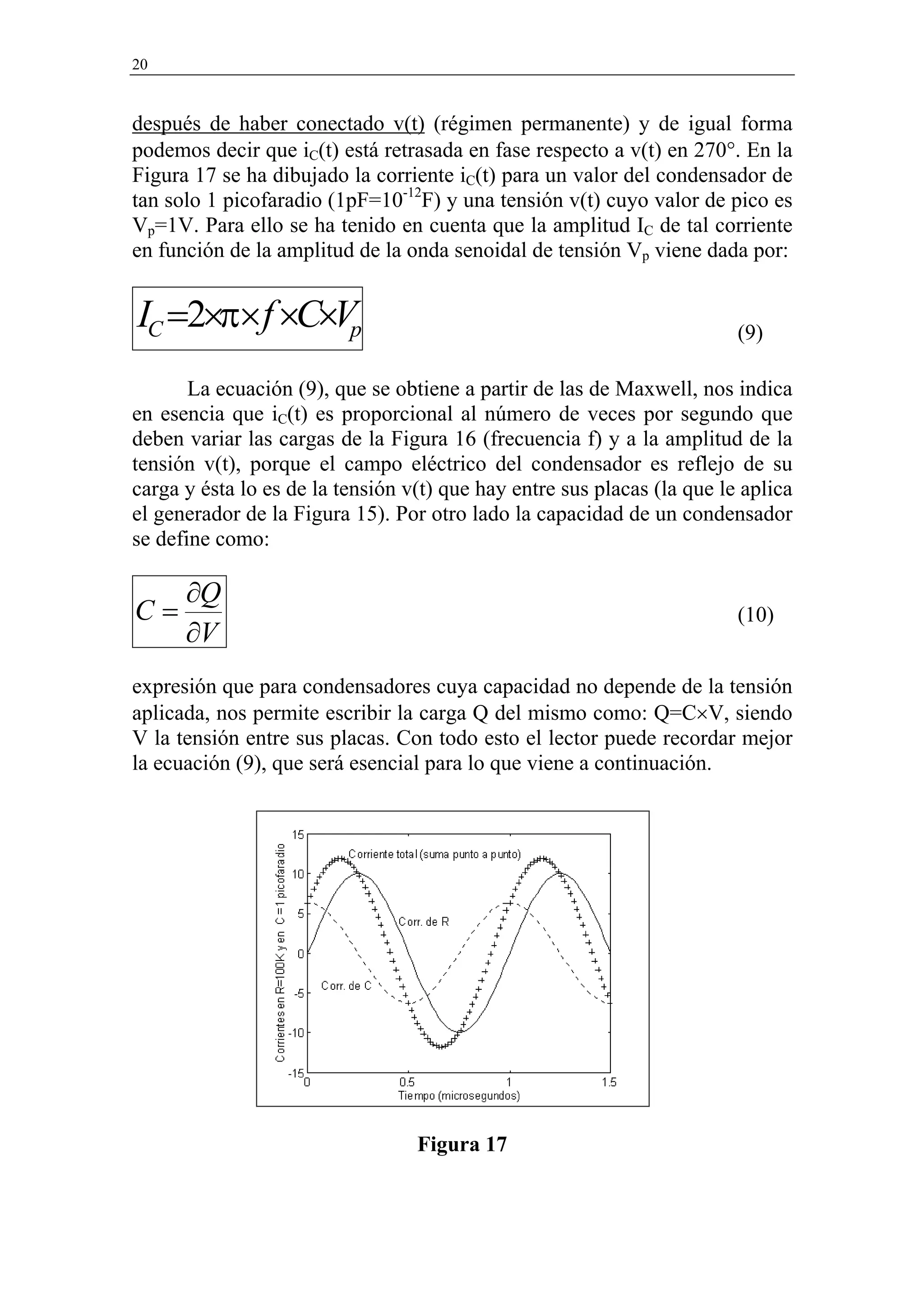
de la Figura 13, donde puede verse que las formas de onda temporales de V](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-16-2048.jpg)



![22
es de +90º como el de iC(t), sino intermedio entre ellos y más cercano a 0º
que a 90º en este caso. Lo anterior proviene de las propiedades de las
funciones seno y coseno (trigonometría). Así θ depende del tamaño relativo
de iR(t) e iC(t) y con los datos empleados en la figura 17 la componente en
fase iR(t) domina (0°<θ<45°), pero si C fuese mayor o la frecuencia más
alta, bien podría dominar iC(t), con lo que el desfasaje de i(t) estaría más
cerca de 90° que de 0° (45°<θ<90°).
Aunque podemos anticipar que la forma de obtener la amplitud o el
módulo de i(t) a partir de las amplitudes de sus componentes en fase y en
cuadratura (P=10µA y Q=2πµA≈6.3µA respectivamente) va a ser mediante
el Teorema de Pitágoras, no está de más recordar un poco de Trigonometría
y deducirlo. Así pues, tenemos:
i (t ) = iR (t ) + iC (t ) = P × sen(2πft ) + Q × cos(2πft ) =
P Q
P +Q × 2
2 2
sen(2πft ) + cos(2πft ) (11)
P +Q P +Q
2 2 2
Dada la forma de los factores que multiplican a las funciones seno y
coseno en la ecuación (11) (la suma de sus cuadrados es igual a 1), no hay
inconveniente en denominarlos cos(θ) y sen(θ). De esta forma tenemos:
i (t ) = P 2 + Q 2 × [cosθ × sen(2πft ) + sen θ × cos(2πft )] (12)
i (t ) = P 2 + Q 2 × [sen(2πft + θ )] (13)
y además:
sen θ Q Q
tg θ = = ⇔ θ = arctg (14)
cosθ P P
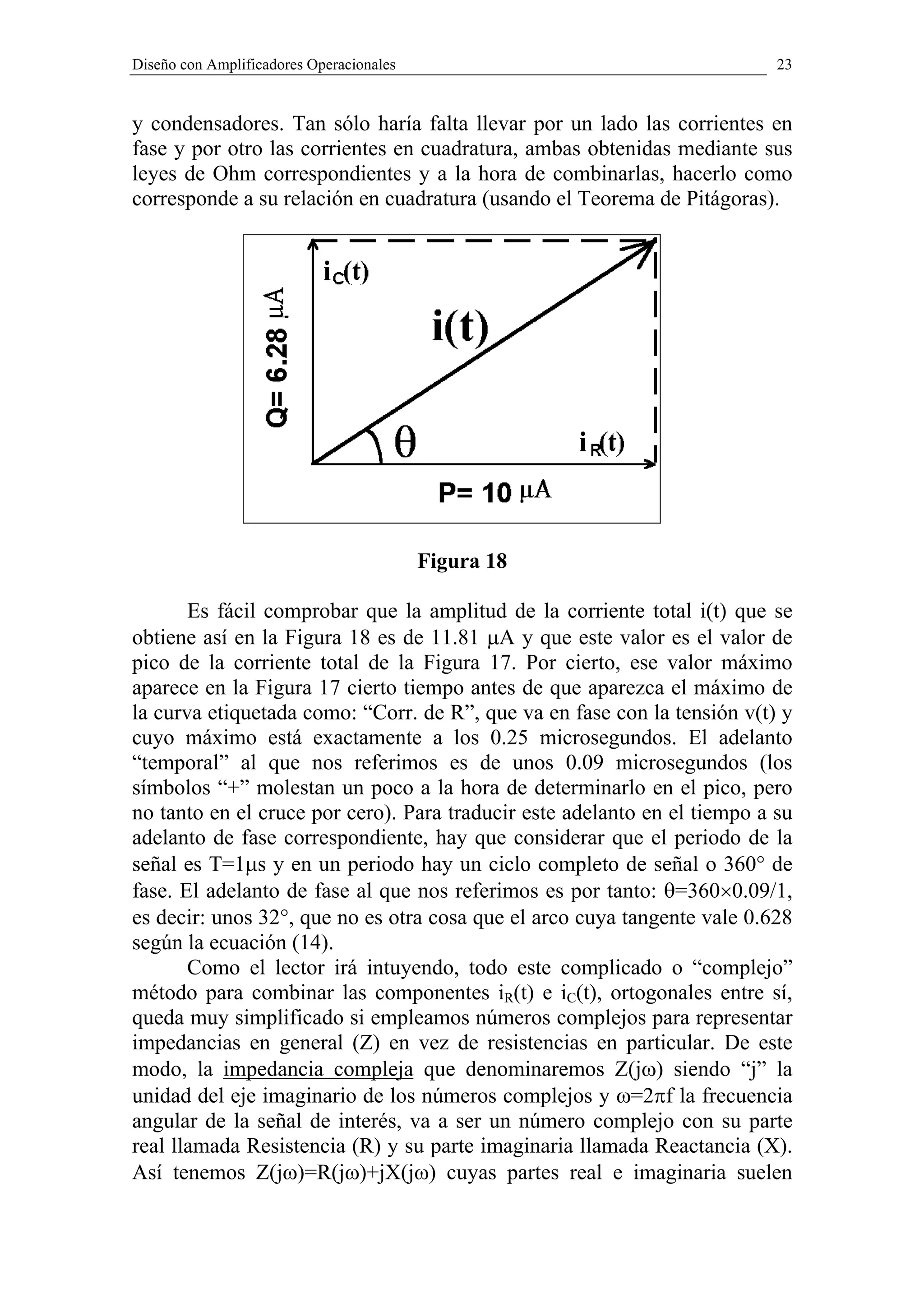
De las ecuaciones (11) a (14) o considerando la ortogonalidad de las
funciones seno y coseno, se puede dibujar la Figura 18 como forma de
memorizar la obtención de i(t) a partir de P=iR(t) y Q=iC(t). El módulo de
i(t) y su defasaje θ salen de forma natural con el Teorema de Pitágoras
aplicado a la figura 18, de modo que sin mucha trigonometría (sólo este
Teorema) podríamos combinar adecuadamente (en rigor sumar) corrientes
desfasadas 90° (en cuadratura entre sí) y manejar circuitos con resistencias](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-22-2048.jpg)


![26
La referencia [4] citada en la Bibliografía es muy aconsejable para el
lector interesado en profundizar en las interesantes propiedades de estas
funciones típicas del régimen permanente senoidal de circuitos LIT y en las
de otras funciones muy relacionadas (variable “s”) que permiten su estudio
en régimen transitorio. Igualmente encontrará esta información en obras
más específicas sobre análisis de circuitos [5].
I.8- Algunos divisores de impedancias interesantes
Con ayuda de la Ley de Ohm generalizada vamos a estudiar unos
divisores de impedancias sencillos, pero de gran utilidad para la educación
del sentido común necesario para abordar con éxito muchos problemas en
Electrónica. El primero de ellos será el circuito R-C paso-bajo de primer
orden, el segundo será su versión paso-alto y el tercero será el que
podríamos denominar R-C paso-banda del oscilador en puente de Wien, un
circuito muy interesante con Amplificadores Operacionales.
La figura 19 resume el enfoque de impedancias y tensiones
complejas (módulo y fase) que emplearemos para estudiar estos circuitos:
Figura 19
Empleando la Ley de Ohm generalizada, la señal de salida Vo(jω) (su
módulo y su fase) vendrá dada por la ecuación generalizada equivalente a
la ecuación (7), es decir:
Z 2 ( jω )
Vo ( jω ) = × Vi ( jω ) (22)
Z1 ( jω ) + Z 2 ( jω )
La ecuación (22) es válida con las mismas consideraciones que se
hicieron para la ecuación (7): que la tensión de salida fuese muestreada sin
provocar corriente de salida. Esto requiere que el módulo de la impedancia
del circuito que se conecte a la salida ZM (jω) sea enorme o, si no es así,
que su efecto de carga ya esté incluido en Z2 (jω).](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-26-2048.jpg)

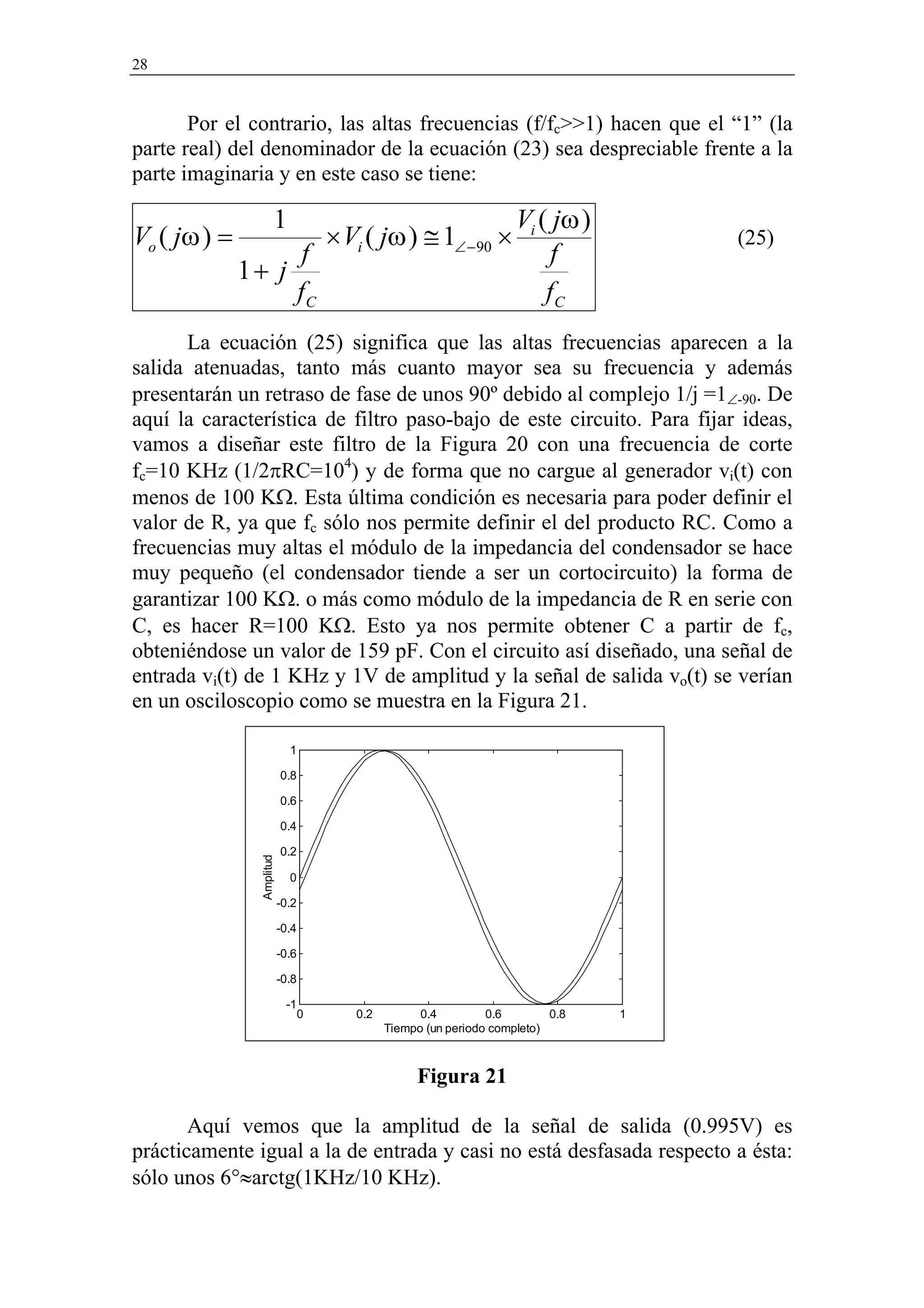
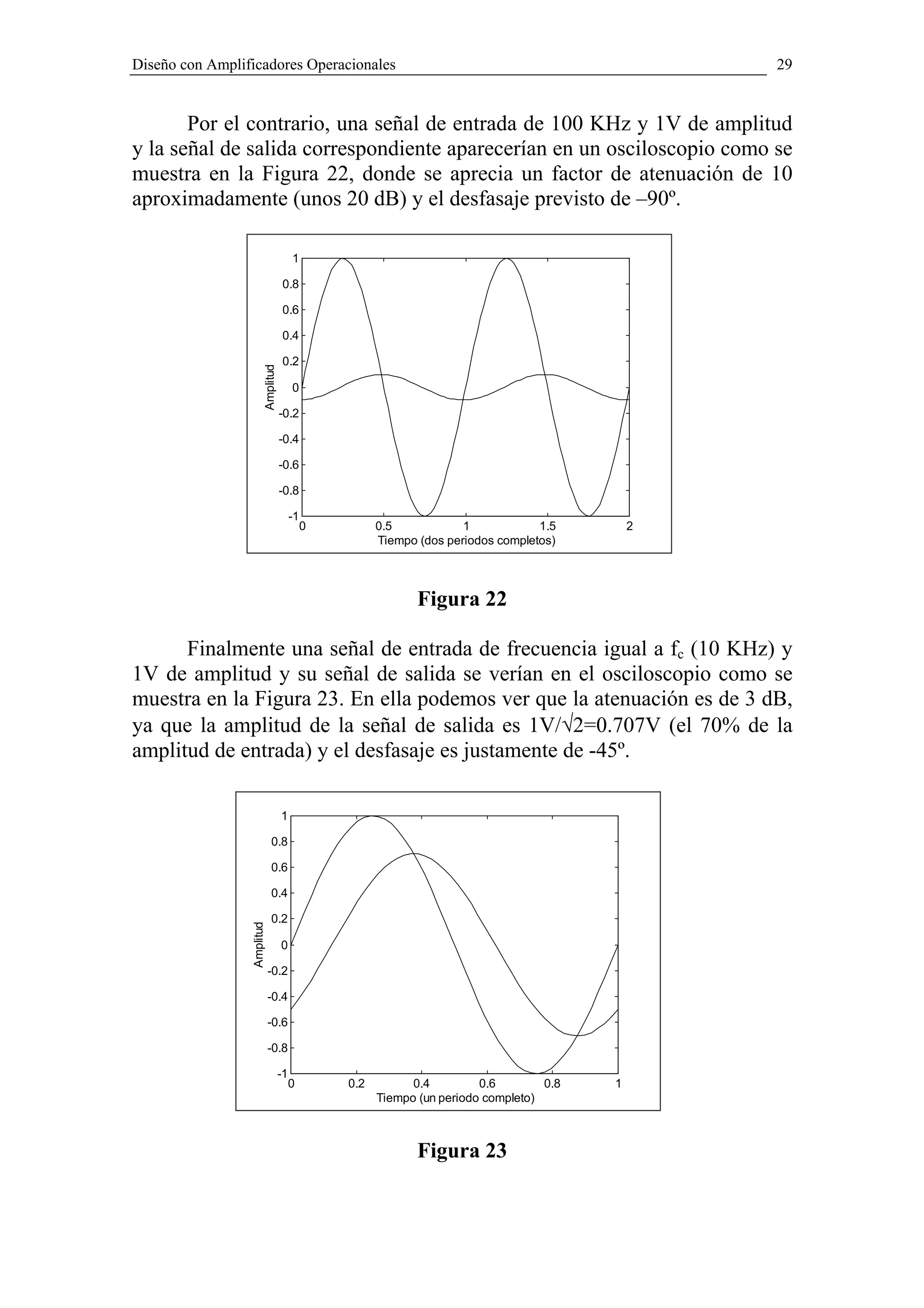
![30
El paso de las señales Vo(jω) y Vi(jω) desde el dominio de la
frecuencia donde tienen la forma compleja M∠θ (siendo M su amplitud y θ
su fase respecto a una referencia dada) hasta el dominio del tiempo para
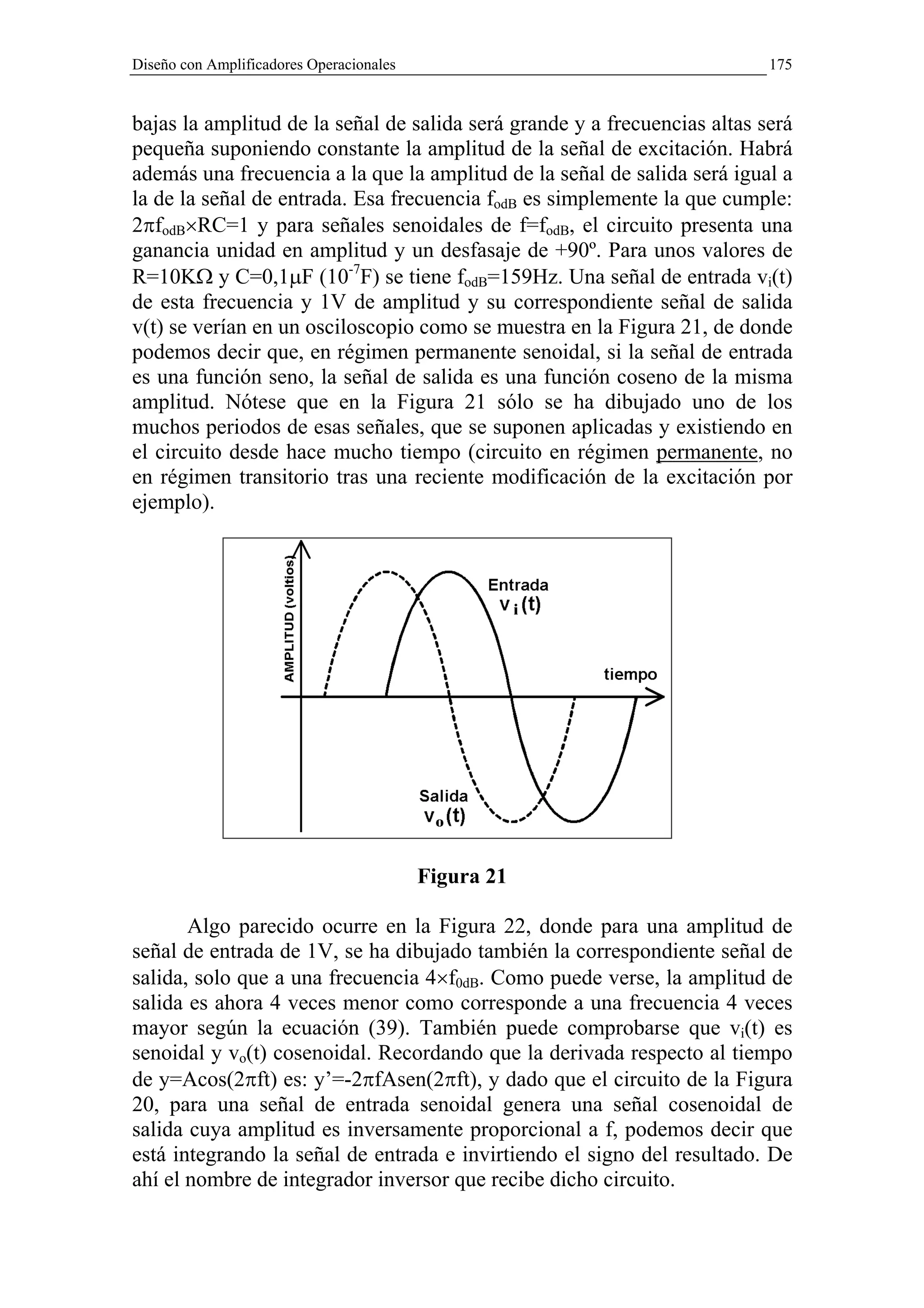
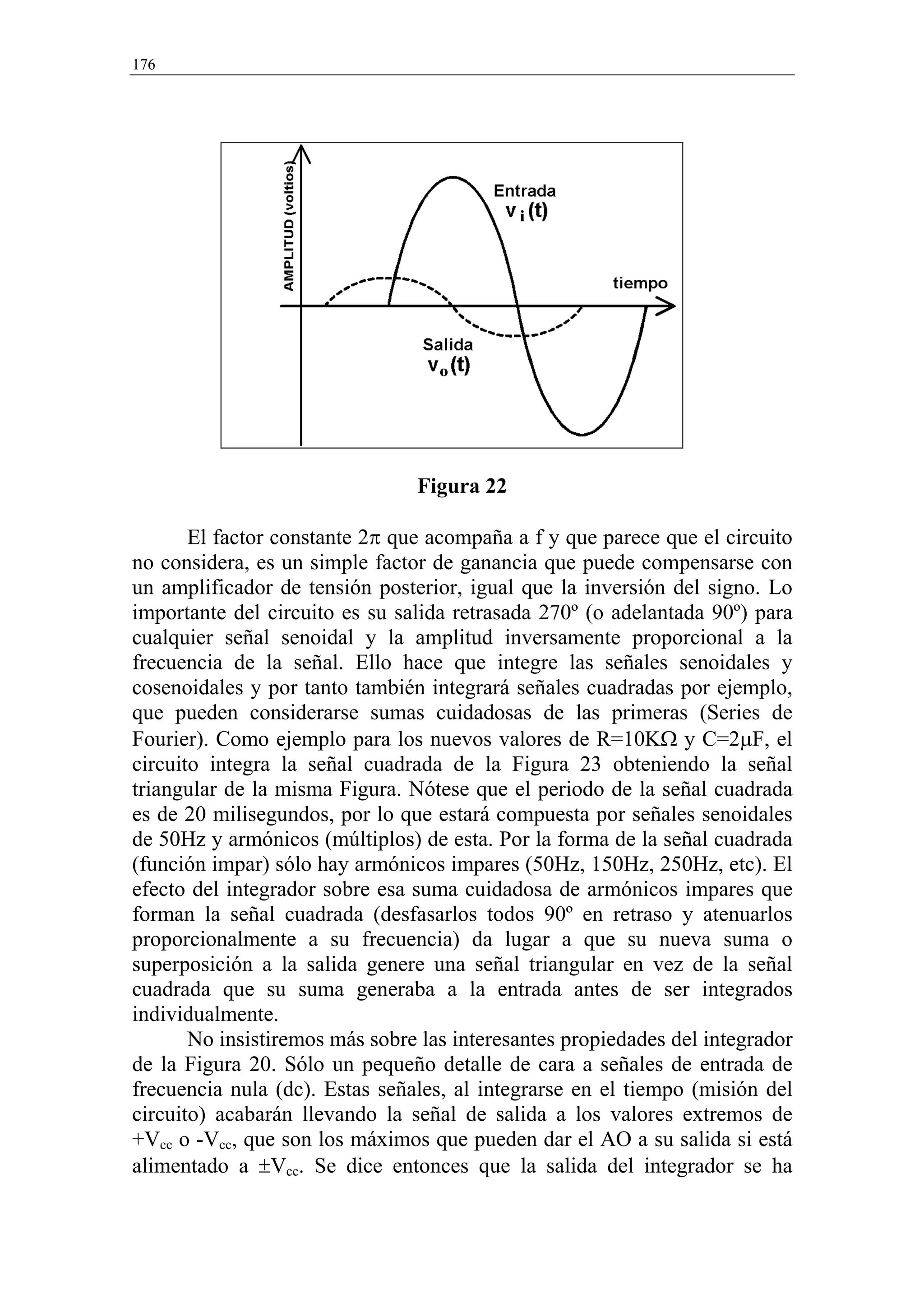
obtener vo(t) y vi(t) ha sido necesario para obtener las Figuras 21, 22 y 23.
Ello consiste simplemente en suponer la excitación senoidal y con fase
cero: vi(t)=A×sen (2πft), por lo que vo(t) es otra onda senoidal con su
amplitud B=A/[1+(f/fc)2]1/2 y cierto retraso de fase dado por: arctg(f/fc),
ambas evaluadas a partir de la ecuación (23).
Este comportamiento de la ganancia Vo(jω)/Vi(jω) en función de la
frecuencia (cuyo aspecto en el tiempo hemos visto en las figuras 21 a 23)
queda plasmado en el Diagrama de Bode de la Figura 24. En esta gráfica, el
módulo de la ganancia se representa mediante las dos rectas asintóticas de
las expresiones (24) y (25) que se cruzan justo en fc. La fase de la ganancia
quedaría razonablemente representada por tres rectas asintóticas, dos de
ellas horizontales a 0º (bajas frecuencias) y a -90º (altas frecuencias) y una
tercera con pendiente de -45º por cada década en frecuencia y que pasase
por -45º de desfasaje en fc. Nótese además la pendiente de -20 dB/década
(atenuación) en la asíntota del módulo para frecuencias altas.
Figura 24](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-30-2048.jpg)
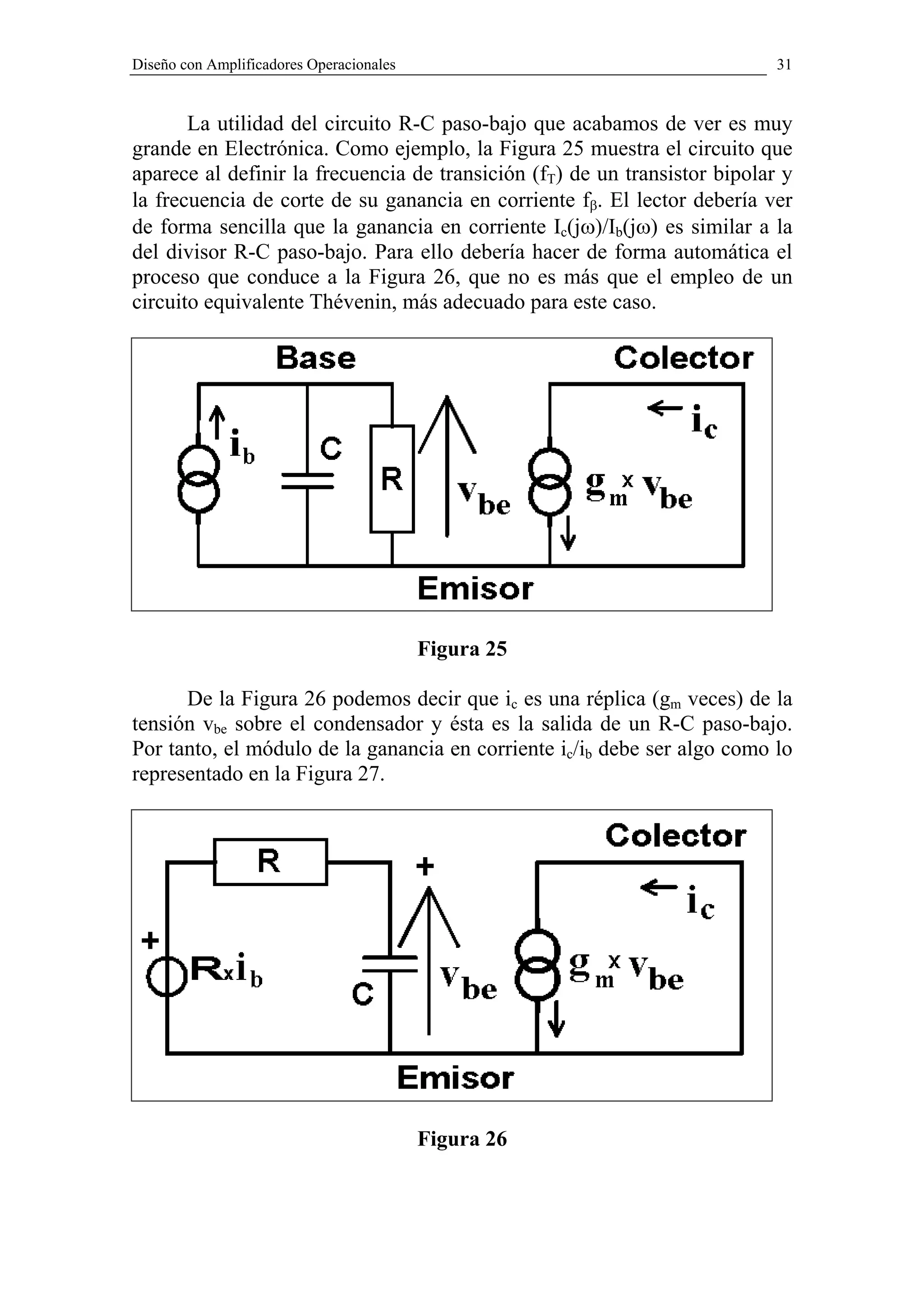
![32
En la Figura 27 se observa que por debajo de fβ=10MHz la ganancia
de corriente Ic(jω)/Ib(jω) es constante e igual a: gm×R=100 en este caso. Sin
embargo, a partir de 10MHz esa ganancia empieza a disminuir a razón de
un factor 10 (20dB) por cada factor 10 (década) que varíe la frecuencia, de
modo que a f=1GHz (109 Hz) tal ganancia ha caído hasta 1 (0dB). Según
esta gráfica, la frecuencia de transición de este transistor sería fT=1GHz y la
frecuencia de corte para su ganancia en corriente sería: fβ=10MHz. Sin
entrar en muchos detalles para no alargar este ejemplo, ese transistor podría
ser utilizado como amplificador, con una configuración circuital adecuada,
hasta algunos cientos de MHz. Remitimos al lector interesado en estos
temas de transistores a obras como [6] donde se tratan con detalle.
Figura 27
El ejemplo anterior sobre la fT de un transistor es sólo uno de los
muchos casos en Electrónica en los que la función de transferencia del
divisor R-C paso-bajo encuentra aplicación directa. Hay muchos más casos,
como puede ser el de la respuesta en frecuencia de un lazo enganchado en
fase (PLL) utilizado para demodular FM, la respuesta en frecuencia de un
amplificador cuando viene limitada por un condensador que aprovecha el
efecto Miller, etc. en los que una buena comprensión por parte del lector de
esta función de transferencia R-C paso-bajo de primer orden, será de gran
utilidad.](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-32-2048.jpg)

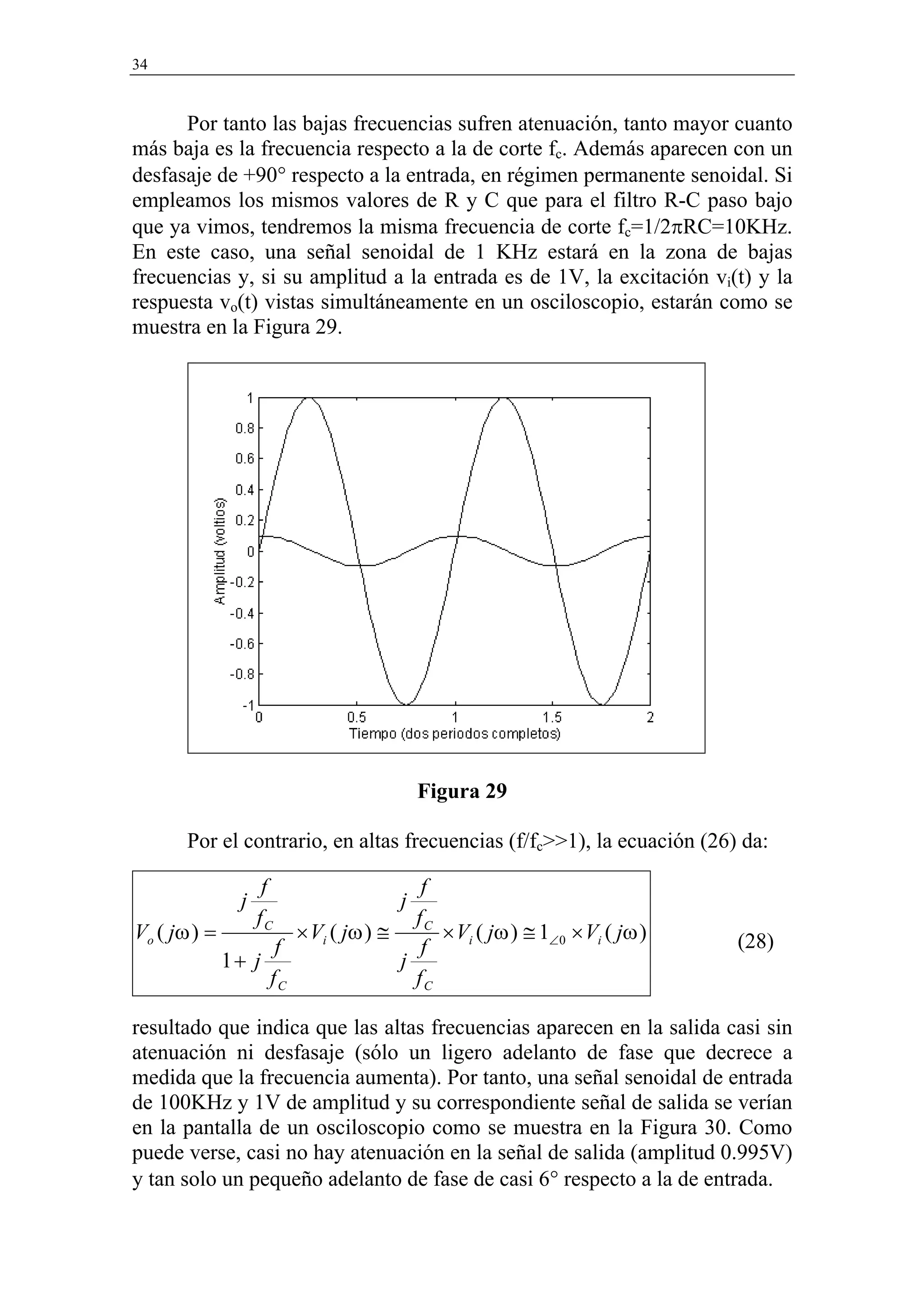
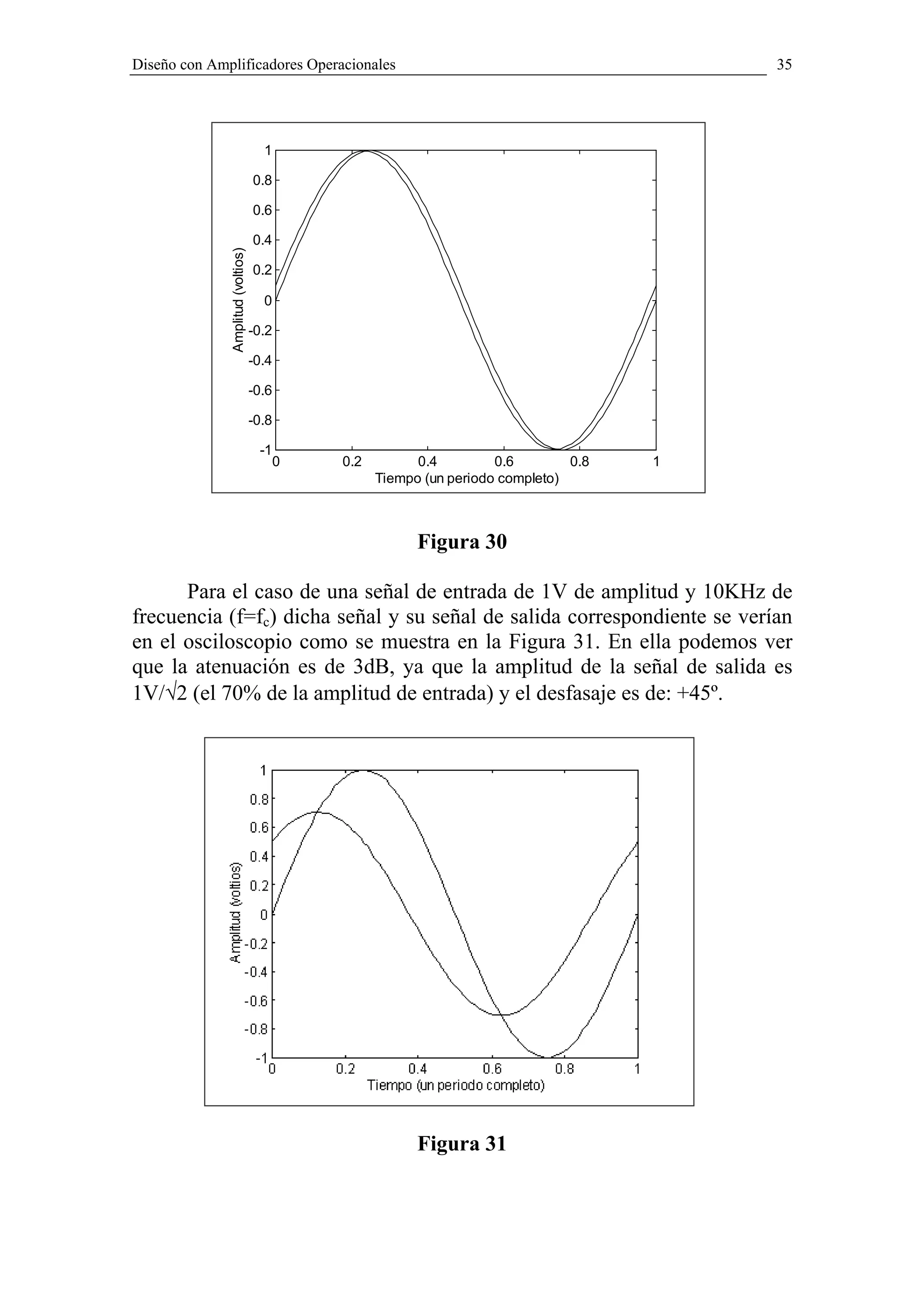















![54
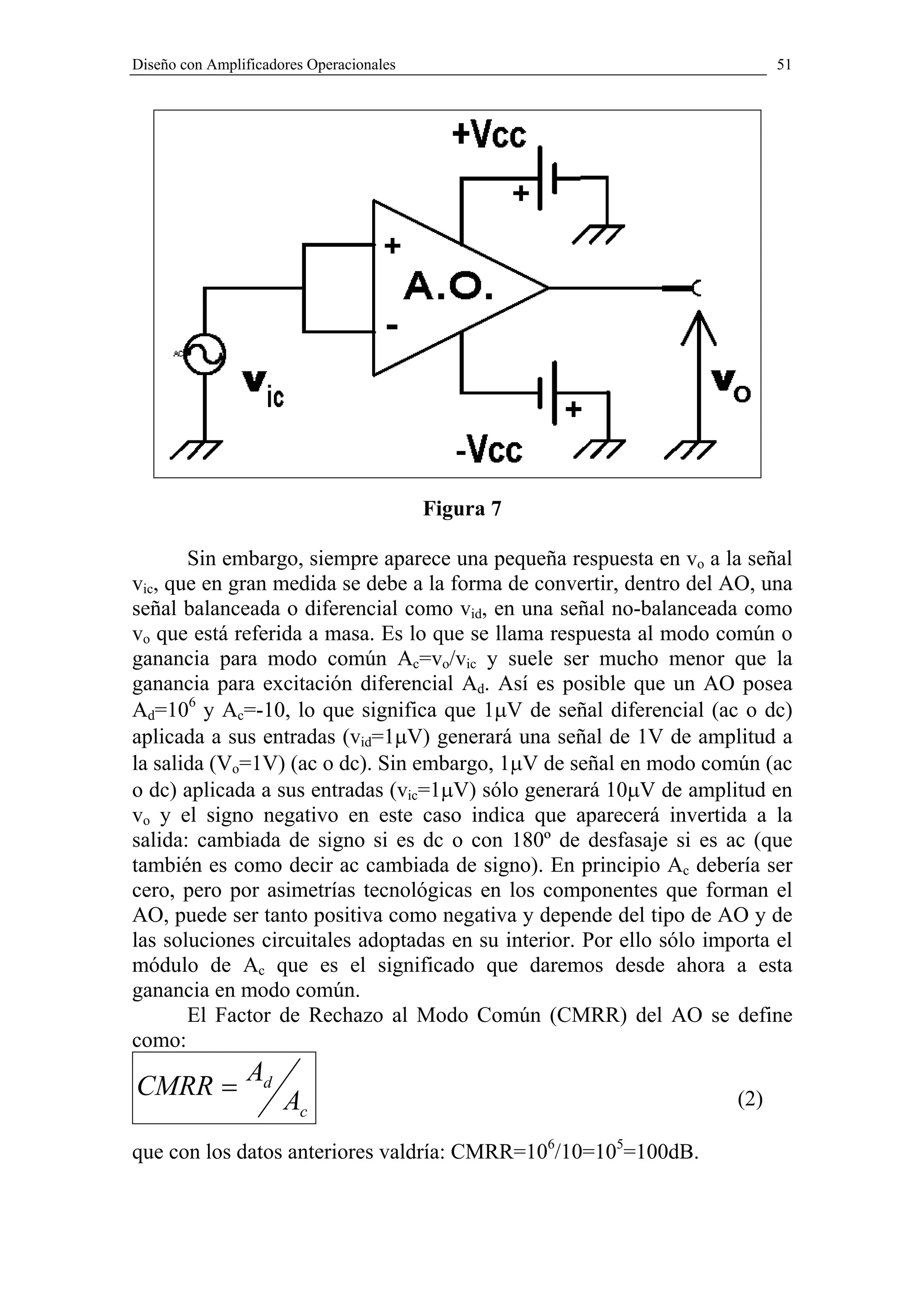
salida que permite manejar tensiones y corrientes a la salida de cierta
importancia (algunos voltios y decenas de mA en AO de propósito general
y decenas de voltios y algunos amperios en AO especiales).
Aunque éste es el tipo de AO que más emplearemos, hay que decir
que existen otros tipos de Amplificadores integrados como son los AO de
Transconductancia (OTA), los AO con entradas en Corriente (llamados
amplificadores Norton) y los AO preparados para ser realimentados en
corriente. Remitimos al lector interesado en ellos a referencias como [6],
[7], [8] y [14] porque no entraremos en su estudio dado nuestro objetivo de
que el lector asimile, en los ampliamente utilizados AO de Tensión, los
conceptos de Realimentación Negativa y Positiva. Una vez logrado esto, el
propio lector podrá adaptarlos a esos otros Amplificadores Operacionales.
Tan sólo daremos aquí, debido a su gran parecido con los AO, el circuito
equivalente simplificado de los OTA que es el que aparece en la Figura 10.
Figura 10
A la vista del circuito de la Figura 10, podríamos decir que es similar
al de la Figura 9, o que se ha obtenido de aquél transformando el circuito
equivalente serie de salida en un equivalente paralelo o Norton, con lo que
el generador de salida es ahora uno de corriente controlado por tensión a
través de la transconductancia gm (de ahí: Operational Transconductance
Amplifier). Pues bien, aunque ello podría ser cierto desde el punto de vista
circuital, hay una importante diferencia estructural entre un AO y un OTA.
De forma resumida podríamos decir que el OTA es un AO al que le falta la
etapa de salida, de forma que su resistencia de salida estaría por encima de](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-54-2048.jpg)
![Diseño con Amplificadores Operacionales 55
la centena de kΩ en lugar de ser inferior al KΩ como en los AO. De hecho,
considerando este detalle sobre la Ro mucho más alta en los OTA que en
los AO, su empleo circuital no difiere mucho conceptualmente.
Las Figuras 11 y 12, tomadas de [9], muestran las estructuras
internas bastante simplificadas de un AO (LH0024) y un OTA (LM3080)
típicos y se han incluido para dar una idea al lector sobre los componentes
internos de estos circuitos integrados, que como puede verse, utilizan un
par diferencial como etapa de entrada. Esa etapa amplifica la pequeña
diferencia de tensión (Vid) que haya entre las entradas inversora (-) y no
inversora (+), y el resto del circuito proporciona tanto ganancia adicional
como el circuito de salida referido a masa que tienen estos dispositivos.
Según la tecnología empleada en el diferencial de entrada, los requisitos
necesarios para que esa etapa de entrada funcione varían mucho. Así, con
tecnología bipolar, habrá que prever caminos adecuados para que fluyan las
corrientes de base de los transistores bipolares del diferencial de entrada.
En otras palabras: esas patillas (+) y (-) no pueden estar “al aire”, ya que
muy probablemente en estas condiciones no existirá el AO que esperamos,
al no estar bien polarizado el par diferencial de entrada. Ello será así
aunque hayamos conectado las tensiones de alimentación +Vcc y –Vcc al
AO. Sin embargo, en circuitos con alguna realimentación, es habitual que
esas corrientes fluyan a través de resistencias empleadas para realimentar el
AO, por lo que el diseñador casi no suele preocuparse de ello.
Figura 11](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-55-2048.jpg)







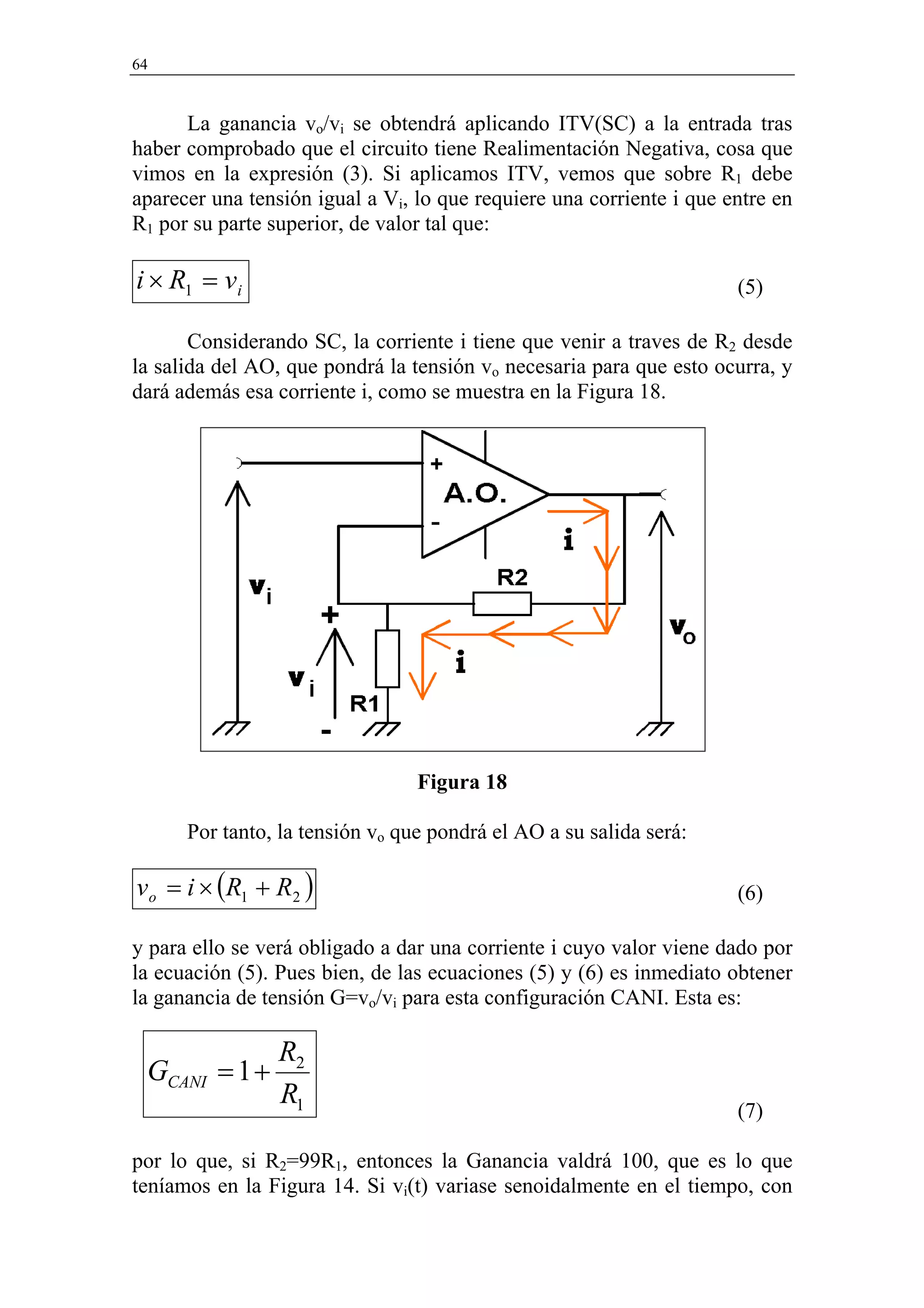





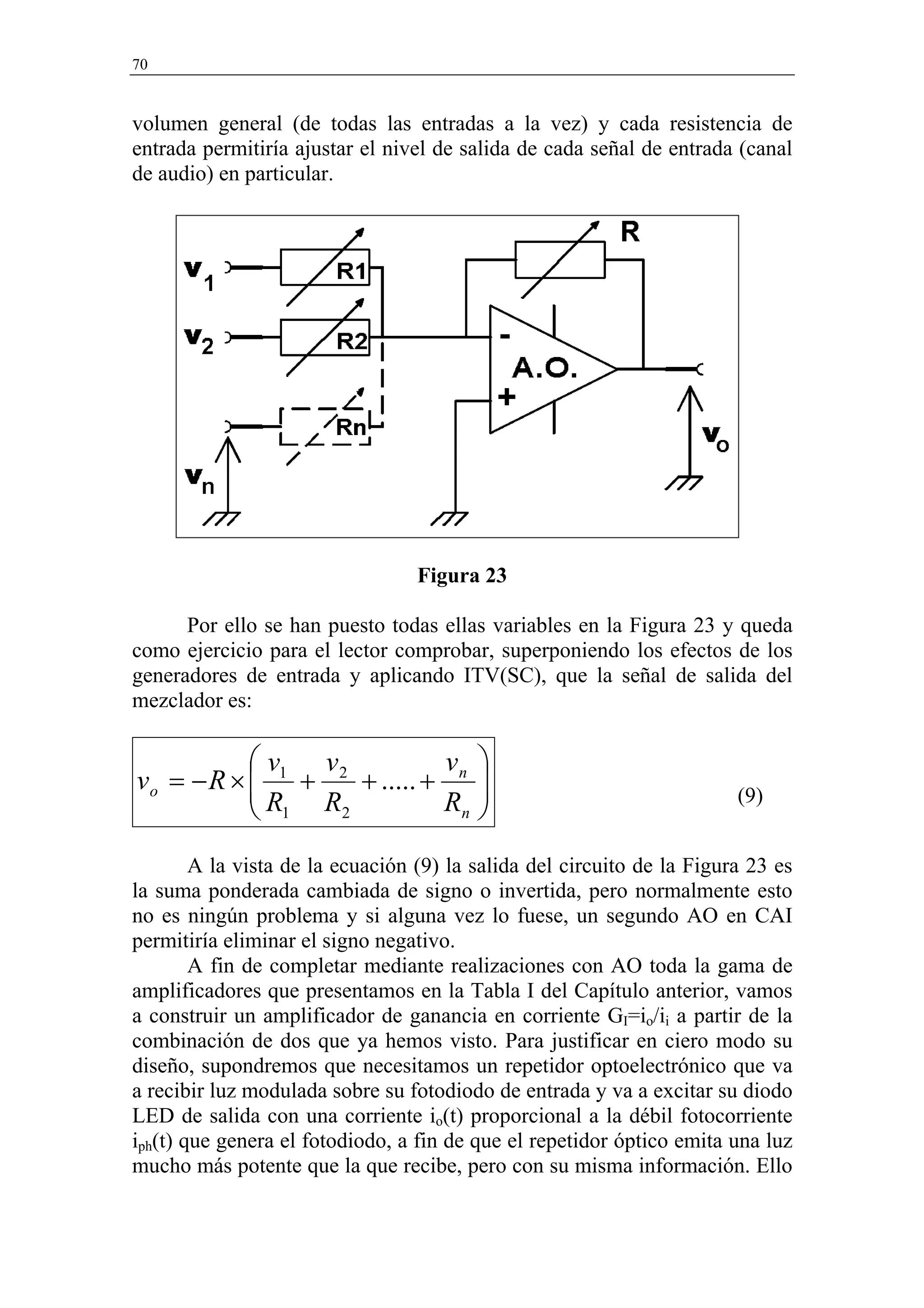


![Diseño con Amplificadores Operacionales 73
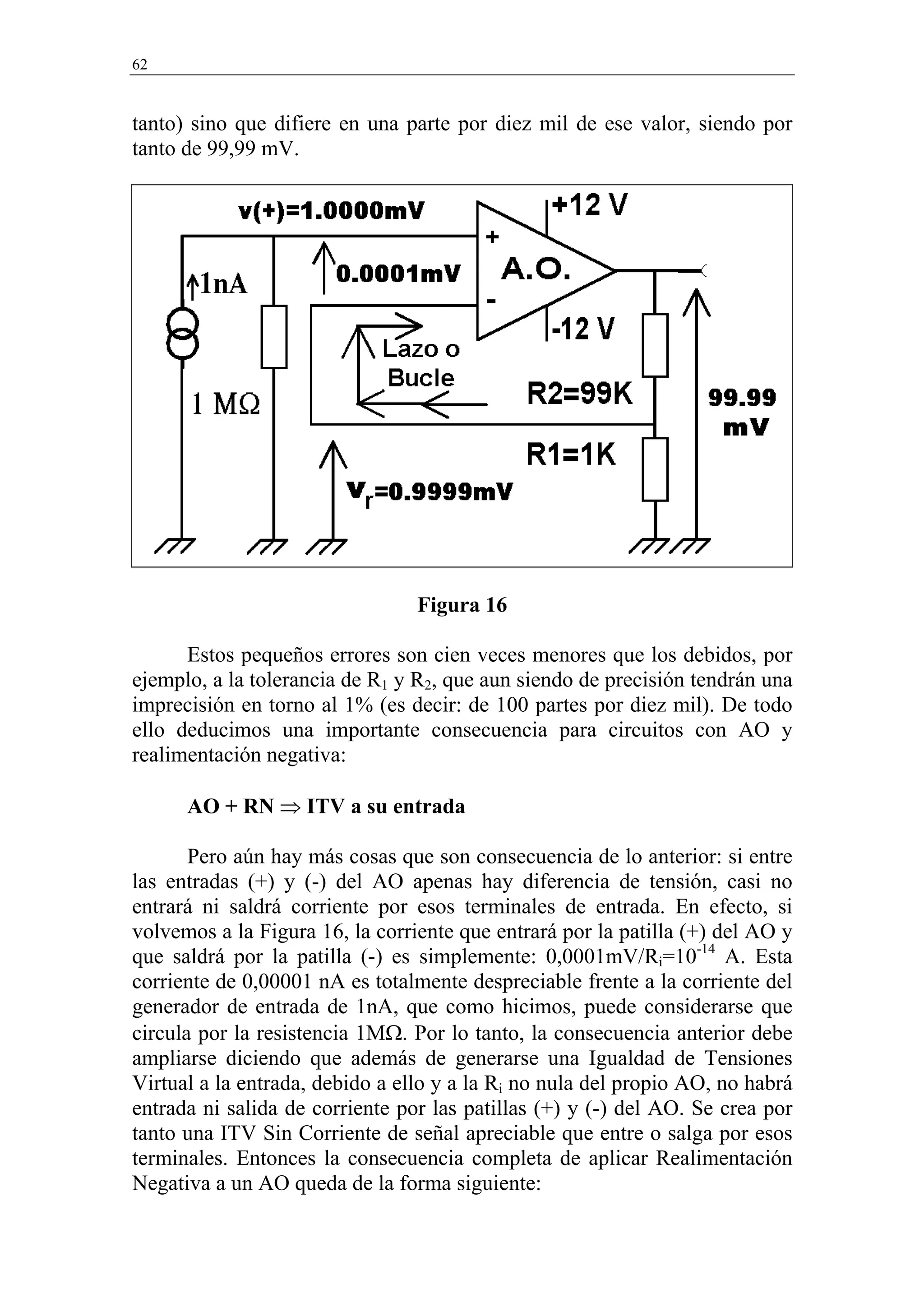
Mostremos en primer lugar la Realimentación Positiva (RP) que
tiene el circuito de la Figura 25. Se hace de forma similar a como hicimos
en la Figura 14 para obtener la expresión (3). Suponiendo, igual que
entonces, que la entrada vi no varía o que es nula mientras hacemos el
razonamiento, veamos cómo reaccionará el circuito ante una variación de la
tensión de salida por ejemplo. Si vo aumentase debido a cualquier causa
externa como puede ser un pico de tensión (ruido) en el circuito, la tensión
vr que es una muestra o fracción de vo también aumentará, en menor
medida pero lo hará. Si vr aumenta, la tensión diferencial de entrada al AO
[v(+)-v(-)] aumentará y, debido a la ganancia Ad del AO esto hará aumentar
vo de nuevo y así sucesivamente. Por tanto, una perturbación en cualquiera
de las señales internas del circuito es aumentada indefinidamente por éste,
a diferencia del caso con RN en el que esa perturbación tendía a ser
anulada. En nuestro caso con RP escribiríamos:
vo↑ ⇒ vr=v(+)↑ ⇒ vε↑ ⇒ vo↑↑ ⇒ vε↑↑ ⇒ vo↑↑↑ etc. (12)
La expresión (12) contiene un primer aviso de lo que se denomina
“regeneración” en este tipo de circuitos con RP que son capaces de generar
señales en ausencia de señal de entrada. En efecto, aunque en la Figura 25
parece que existe un punto de equilibrio con todas las tensiones nulas (vi,
vo, vr y vε) ese equilibrio no es estable como sucede, bajo RN, en el circuito
de la Figura 17. Así, aun cuando en el de la Figura 25 tuviéramos: vi=0,
vo=0, vr=0 y vε=0 en cierto instante, esta situación desaparecería en seguida
por la presencia del inevitable ruido electrónico.
Dada la imposibilidad de alcanzar el cero absoluto de Temperatura (y
de que el circuito funcionase a T=0K), siempre habrá ruido térmico [10] en
R1 y R2 o en cualquier resistencia interna del AO. Ese ruido se manifiesta
precisamente haciendo que ninguna tensión entre los extremos de una
resistencia pueda tener un valor constante. Siempre habrá una pequeña
fluctuación, unas veces positiva y otras negativa, de algún microvoltio o
nanovoltio de amplitud en bornas de una resistencia que no está a cero
grados Kelvin como mostró experimentalmente Johnson [11] y demostró
teóricamente Nyquist [12]. Debido a ello, la tensión vr de la Figura 25
puede en un instante ser de: vr=+1nV (+10-9 voltios). Si las demás tensiones
de la Figura fuesen nulas, tendríamos el AO excitado con vε=vid=1nV
debido al ruido. Como la ganancia del AO era Ad=106 según dijimos, ese
nanovoltio a la entrada será amplificado hasta el milivoltio (un millón de
veces) a la salida. Si pensamos que el divisor R1-R2 atenúa por 100 como el
de la Figura 16, (R1=1K, R2=99KΩ), ese mV a la salida en vo se habrá
convertido en 1mV/100=10µV sobre R1 y esto de forma casi instantánea
debido a la rapidez de la electrónica. Por tanto, una tensión de ruido que era
inicialmente de 10-9 V es ahora de 10-5 V y estos 10 µV sufrirán la misma](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-73-2048.jpg)

![76
Figura 27
Para calcular IDIV hemos despreciado la corriente que pueda ir hacia,
o venir de, la entrada (+) del AO. Sin embargo ahora no tendríamos
derecho a hacerlo a menos que demostrásemos que es despreciable, porque
ahora no se produce una ITV(SC) sino todo lo contrario. De hecho la
tensión que IDIV genera en R1 es de +0,11V: el divisor R1-R2 muestrea una
tensión vo= +11V y sobre R1 presenta la centésima parte de esa tensión. La
corriente que debido a esa tensión tendería a entrar hacia la entrada (+) del
AO sería del orden de: [v(+)-v(-)]/Ri≈ 0,11/107≈10-8 A. Por lo tanto, sólo
debido a la alta Ri del AO la corriente que absorberá por su entrada (+) es
completamente despreciable frente a IDIV. Nótese la importante diferencia
con el caso en el que había ITV(SC): allí la corriente aún era mucho más
baja porque v(+)-v(-) tendía a cero. Ahora, sólo la alta Ri del AO impide un
consumo apreciable de corriente por la entrada, cosa que con ITV(SC) ello
era debido más a la igualdad virtual de tensiones que al valor de Ri (aunque
éste también ayudaba).
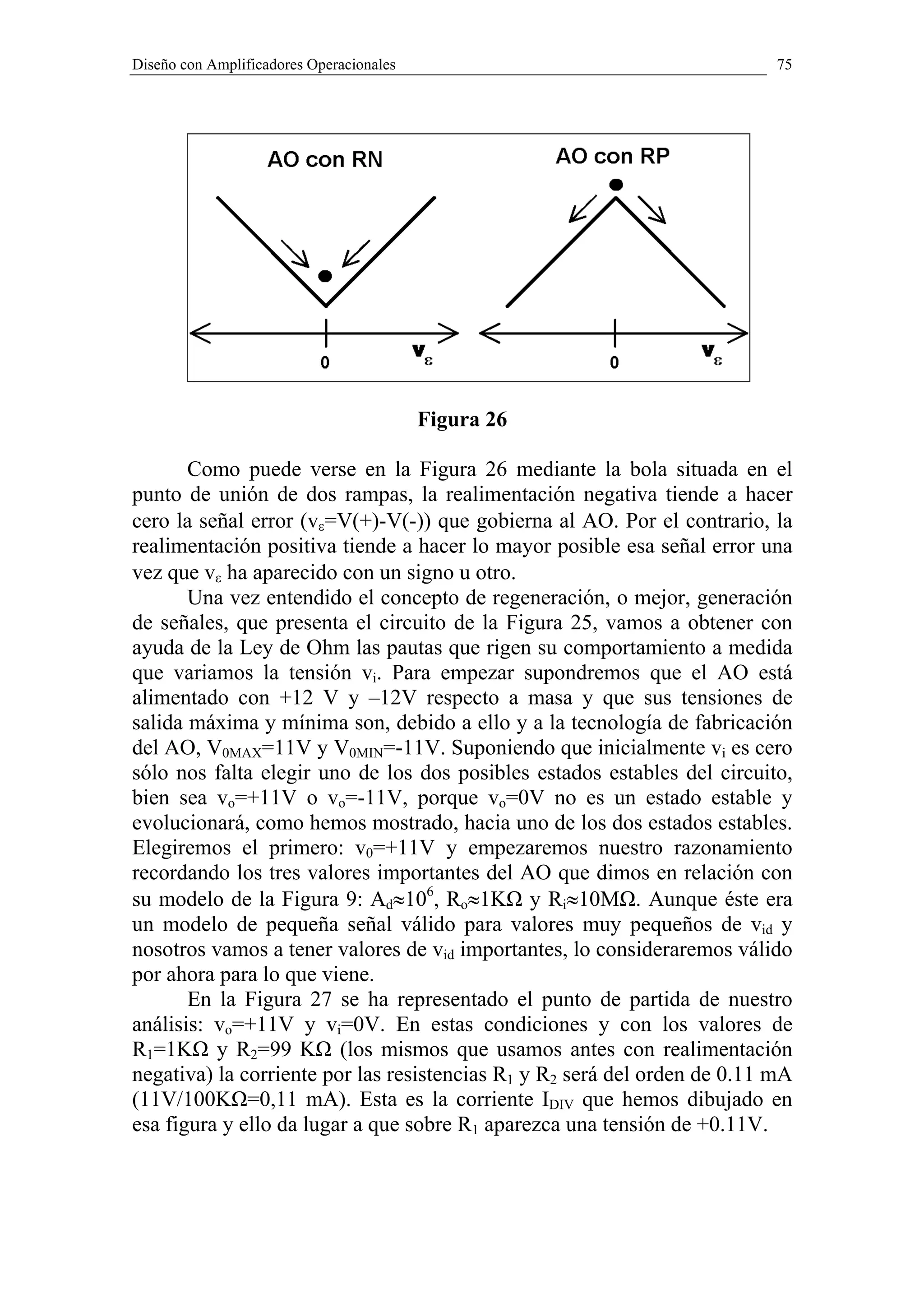
Acabamos de presentar el máximo valor de la tensión en la entrada
(+) del AO que es de: +0,11V. Este valor no es más que el producto de vo
por el factor de atenuación del divisor R1-R2. Es decir:
R1
v(+ ) MAX = voMAX × (13)
R1 + R 2
Este valor es importante porque como veremos enseguida los valores
de tensión v(+) que van a generarse en el circuito al ir variando vi son éste
y su opuesto. Para demostrarlo vamos a ir aumentando el valor de vi desde](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-76-2048.jpg)
![Diseño con Amplificadores Operacionales 77
donde está ahora: vi=0. Es fácil ver que hasta que vi no supere v(+)MAX, el
circuito seguirá en el estado en el que está con vo=+11V. Por ejemplo, si vi
aumenta hasta +0,1V, todavía la tensión v(+) es de +0,11V y como:
v0=Ad×[v(+)-v(-)], el circuito no variará su tensión de salida vo=+11V.
Ahora bien, en cuanto vi sobrepase ligeramente el valor v(+)MAX=0,11V
(por ejemplo vi=0,111 voltios) la tensión de la entrada (-) será 1 milivoltio
mayor que la entrada (+) y esto es suficiente para que la salida vo cambie
bruscamente a –11V. Realmente esto ocurriría con menos diferencia de
tensiones a la entrada que 1mV. Bastaría con 11 microvoltios de diferencia
a favor de v(-) ya que:
Vo=-11V=106×[v(+)-v(-)] ⇒ v(+)-v(-)=-11µV (14)
Como hablar de microvoltios es estar muy cerca de los valores de
tensión de ruido en resistencias como las empleadas a poco ancho de banda
que se considere, se acepta que cuando vi alcanza el valor v(+)MAX de la
ecuación (13), el circuito biestable de las Figuras 25 ó 27 bascula de su
estado estable definido por vo=+11V a su otro estado estable definido por
vo=-11V (tramo B1-B2 de la Figura 28). Esto a su vez hace que la tensión en
la patilla (+) cambie bruscamente al valor:
R1
v(+ ) MIN = voMIN × (15)
R1 + R 2
Este brusco cambio de v(+) hace que, como v(-)=vi es justamente
igual al valor v(+)MAX, la diferencia de tensiones entre las entradas se
amplifique bruscamente, pasando a ser el valor característico siguiente:
R1
∆vε = v(+ ) MIN − v(+ ) MAX = (voMIN − voMAX ) × (16)
R1 + R 2
Aquí vemos claramente que la RP tiende a hacer lo más desiguales
posible las tensiones en las entradas (+) y (-). Con los valores voMAX=+11V
y el atenuador por 100 (R1=1KΩ, R2=99KΩ) la ecuación (16) indica que la
zona de histéresis (luego veremos su significado) es: ∆Vε=-0,22V. Esta
zona es de gran interés si el circuito se emplea como comparador con
histéresis para luchar contra el ruido, como veremos más tarde. Si una vez
que el circuito ha basculado o cambiado de estado vi sigue aumentando, no
sucede nada más (salvo que vi sea tan alto que pueda dañar la entrada del
AO). El circuito permanece en su estado “0” (con vo=-11V).](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-77-2048.jpg)
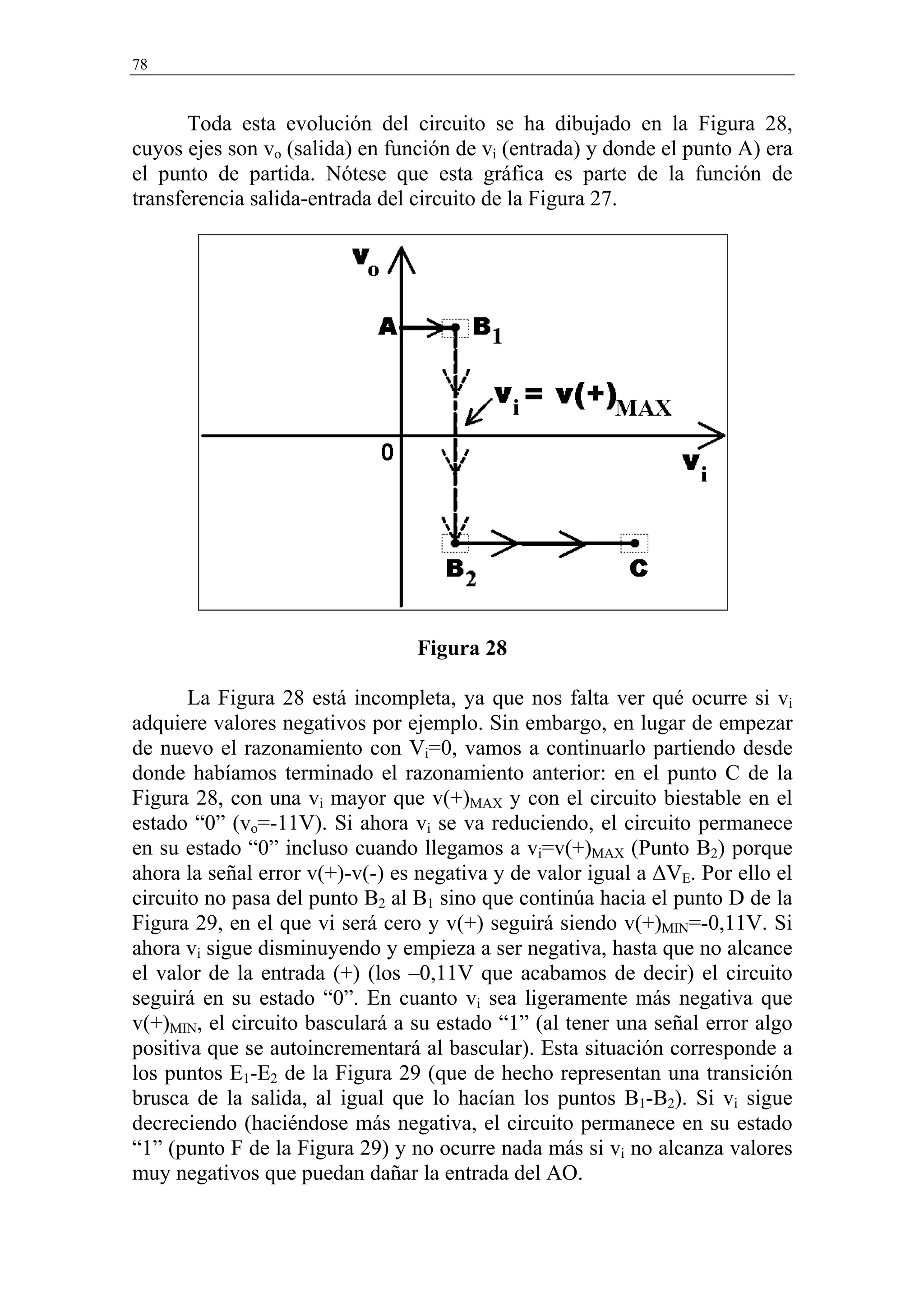

![Diseño con Amplificadores Operacionales 81
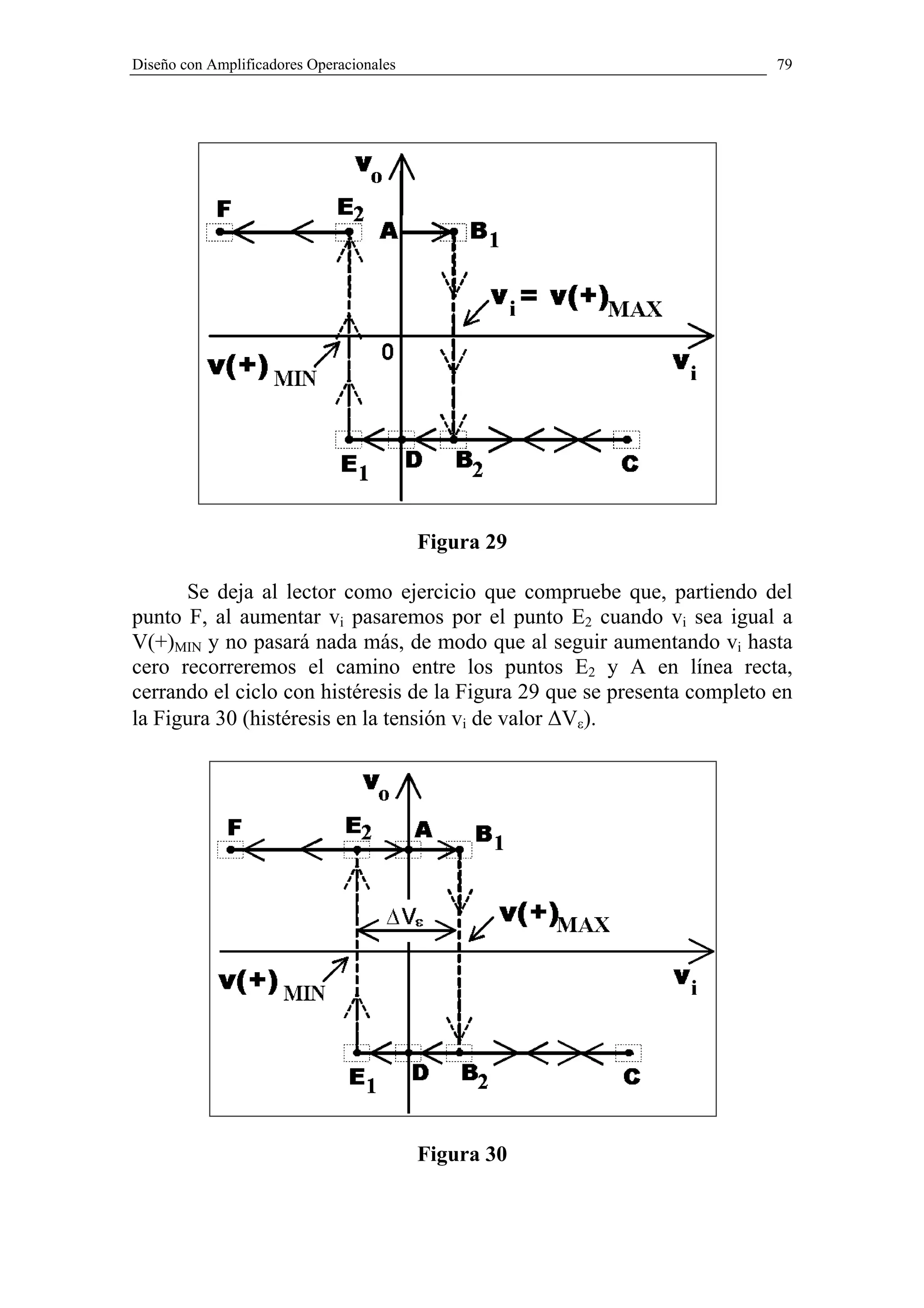
Al estar la señal cerca de cero, los picos de ruido harán que se
produzca una ráfaga de conmutaciones de +Vcc a –Vcc y de –Vcc a +Vcc en
puntos donde los picos de ruido hagan cruzar por cero la señal
[vi(t)+ruido], con lo que no tendremos una buena indicación del cruce por
cero de la señal vi(t) (el punto X). Curiosamente, la realimentación positiva
que hace al circuito generativo le permite también luchar contra los efectos
del ruido mostrados en la Figura 31-b. Si empleamos el comparador con
una histéresis ∆Vε como se muestra en la Figura 32, eliminaremos la ráfaga
de conmutaciones y disfrutaremos además de una ventaja adicional; el
circuito conmutará más deprisa debido a la acción de la realimentación
positiva, porque en cuanto cambia de estado, la entrada diferencial del AO
pasa a estar excitada por una señal que no es un valor cercano a cero de vi,
sino la diferencia entre ese valor casi nulo y uno de los valores v(+)MAX o
v(+)MIN que se realimentan a la patilla (+) del AO. Esto aumenta la rapidez
de evolución de la electrónica interna del AO durante la conmutación.
Figura 32
Tras esta primera aplicación del circuito de la Figura 25 diremos que
recibe el nombre de “comparador Schmitt” (Schmitt trigger) y es la base de](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-81-2048.jpg)













![Diseño con Amplificadores Operacionales 97
2.- Desensibilización de ganancia por el mismo factor: la ganancia G es
(1+Aβ) veces menor que A, pero también es (1+Aβ) veces más estable o
menos sensible a las variaciones relativas de ganancia A.
3.- Modificación de impedancias de entrada y de salida, aumentándola en
un factor (1+Aβ) si la conexión es serie (entrada) y reduciéndola por el
mismo factor si la conexión es paralelo (salida). Más tarde comprobaremos
que esto ocurre tanto a la entrada como a la salida y sólo depende del tipo
de conexión (serie o paralelo).
Otras propiedades circuitales como son: reducción de distorsión,
reducción de efectos debidos a ruido interno, aumento de ancho de banda,
etc, son consecuencia de las anteriores y no entraremos aquí en detalle. El
lector interesado podrá encontrar tratamientos más amplios y con diversos
enfoques, en obras como: [6], [8], [13] y [14].
III.3- Efectos de carga de la red de realimentación
Hasta este momento hemos ido evitando deliberadamente los efectos
de carga de una red sobre otra en el esquema de dos cuadripolos A y β
interconectados en la forma mostrada. Tratábamos así de aproximarnos al
diagrama ideal de la Figura 2, con cajas o bloques que no se molestaban
entre sí. Sin embargo, esto no es posible en Electrónica y para ser capaces
de diseñar bien un circuito con AO y RN, debemos conocer el correcto
manejo de estos efectos de carga. El diagrama de la Figura 2 y su función
de transferencia asociada, la ecuación (3), son un buen ejemplo de algo que
casi todo estudiante capta y entiende, pero cuya implementación real con
circuitos electrónicos pocos dominan. No obstante, viendo de dónde vienen
las cosas, se puede dominar sin mayores problemas el diseño tanto de este
tipo de circuitos realimentados basados en AO, como el de otros que
empleen los diversos dispositivos electrónicos existentes.
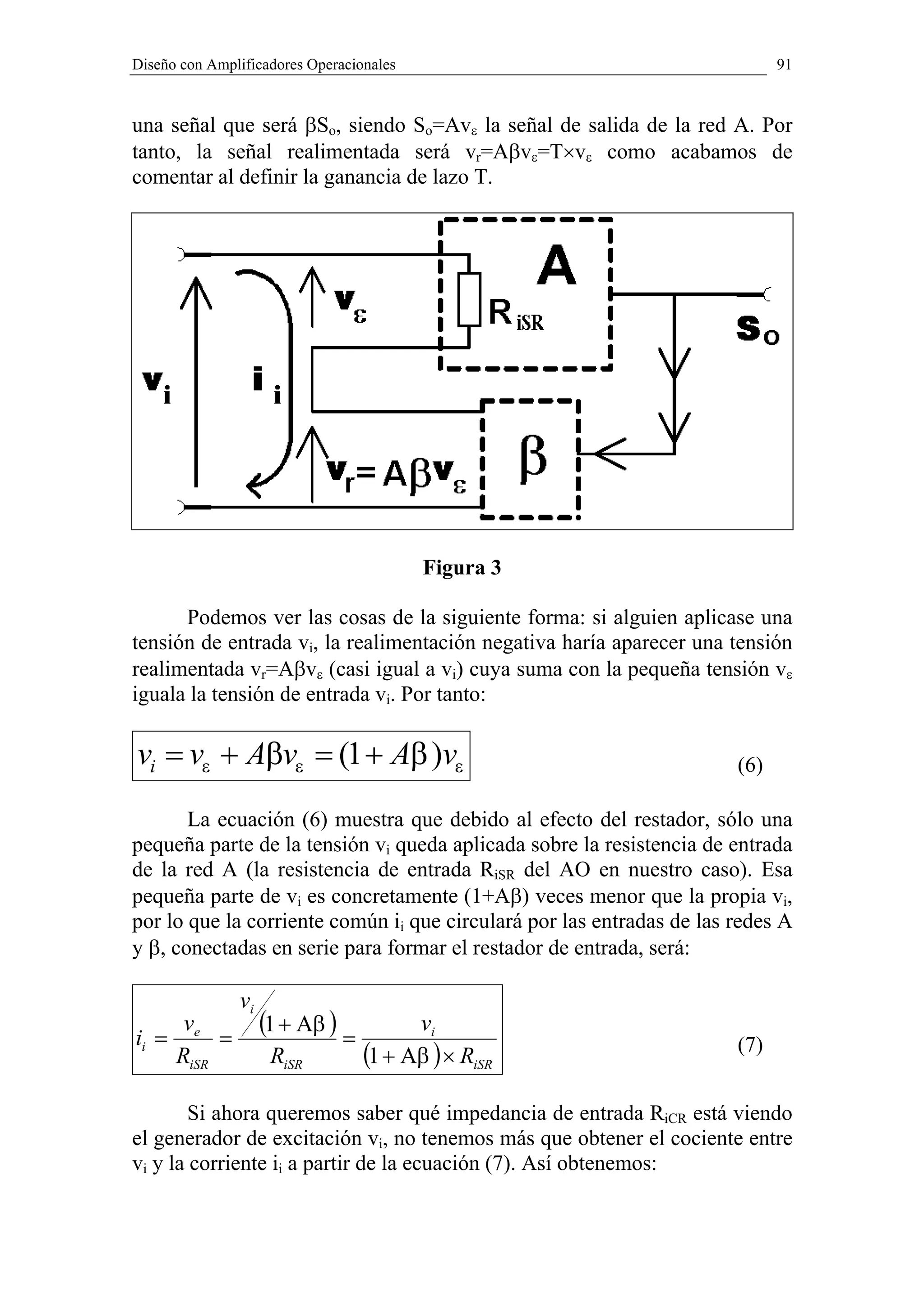
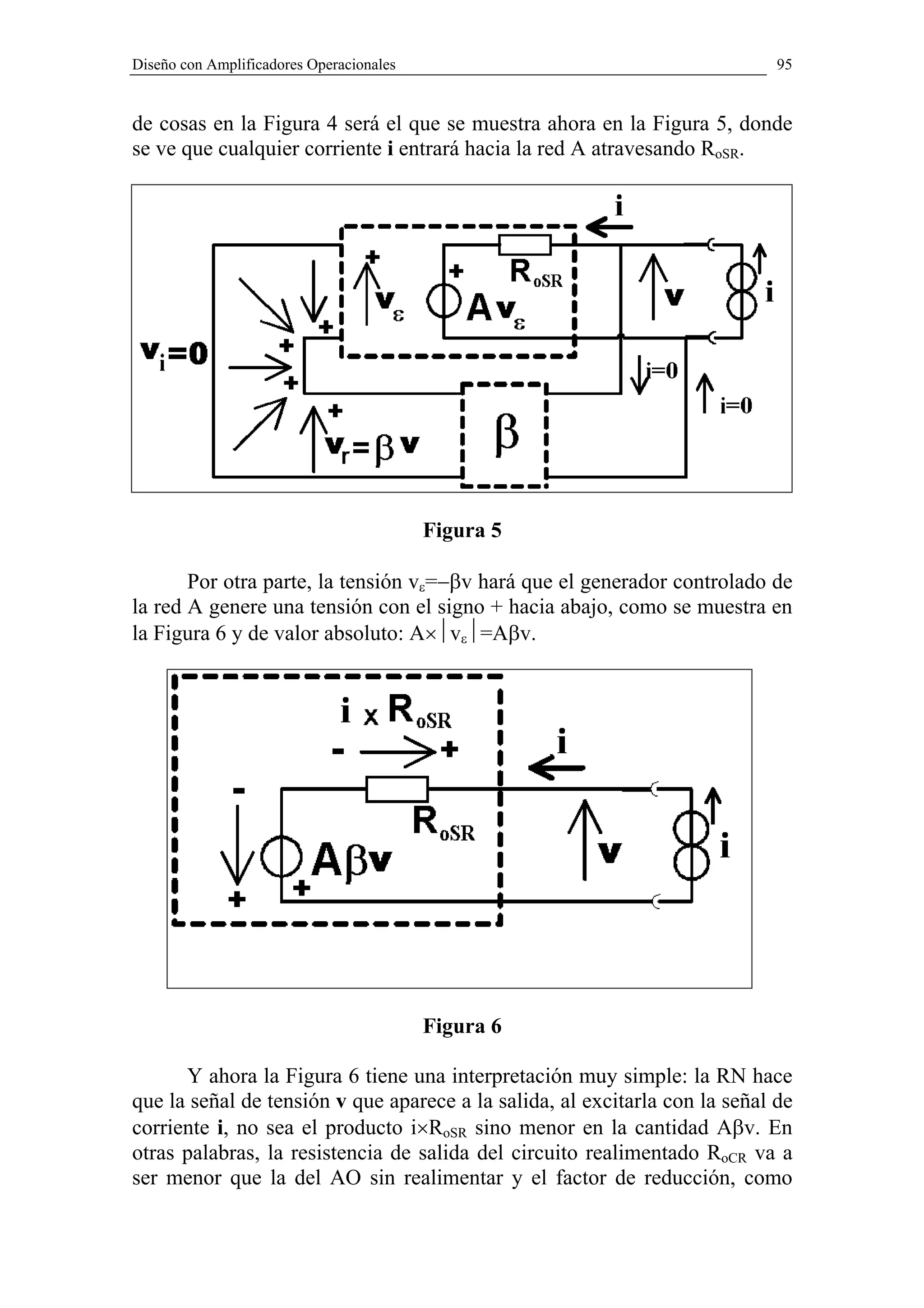
Una vez hecha esta presentación pasamos a ver las “complicaciones”
que acarrea el empleo de una red β tan sencilla como el divisor resistivo del
amplificador de la Figura 17 del Capítulo II. Observando las Figuras 1, 3 y
4 del presente Capítulo vemos que el cuadripolo β y el cuadripolo A están
conectados en serie a la entrada para formar el restador de tensiones y en
paralelo a la salida para tener el muestreador de tensión. Esto significa que
la tensión de salida vo es una excitación común a los dos cuadripolos A y β,
o mejor dicho: a los tres cuadripolos existentes, que son:
1- El de transferencia directa o red A
2- El de transferencia inversa, de realimentación, o red β.
3- El global de ganancia G al que equivale la conexión de los otros
dos y que posee tanto transferencia directa como inversa, aspecto
éste que se olvida frecuentemente.](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-97-2048.jpg)









![Diseño con Amplificadores Operacionales 109
que hicimos allí para obtener la ecuación (10) y su versión generalizada la
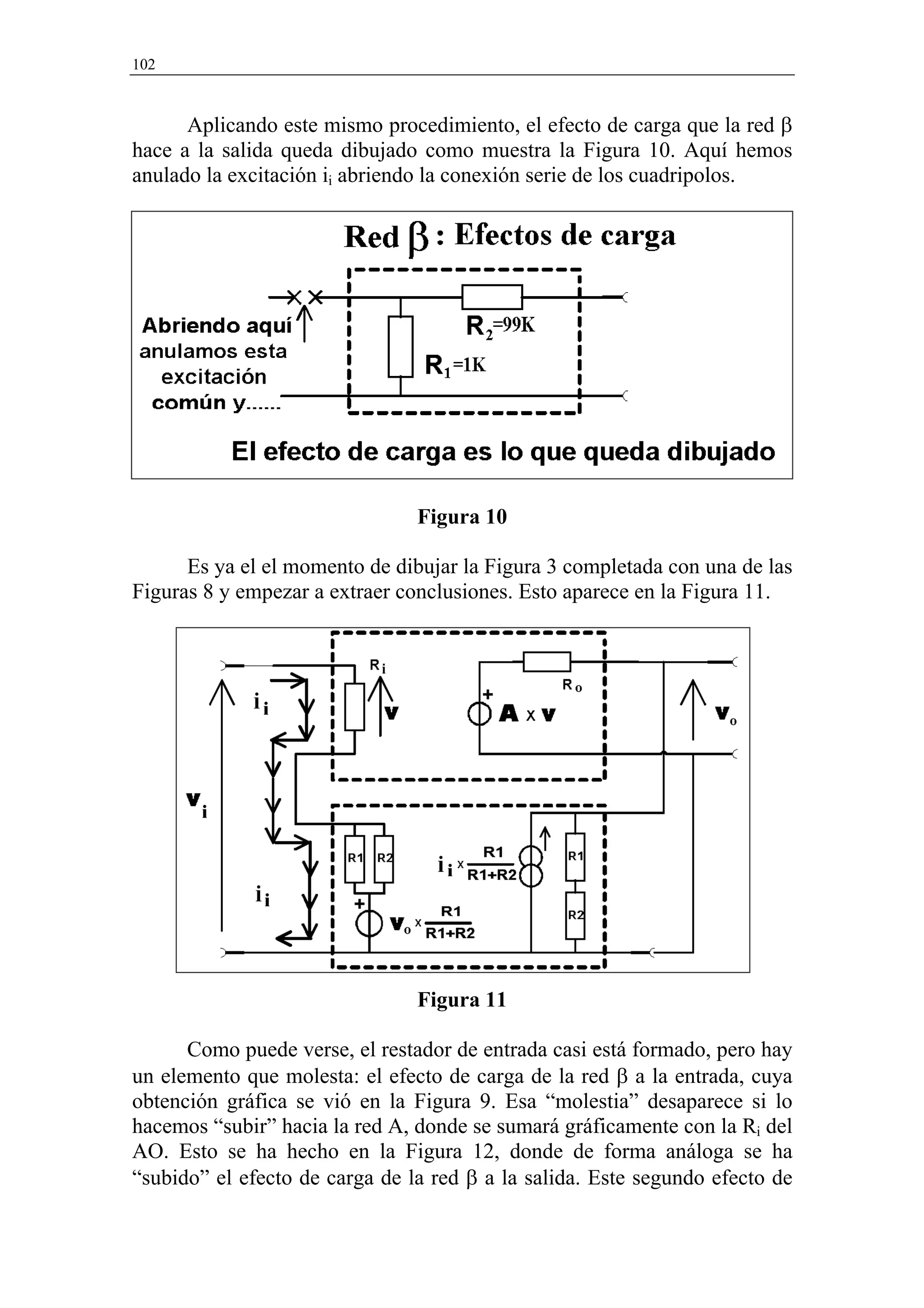
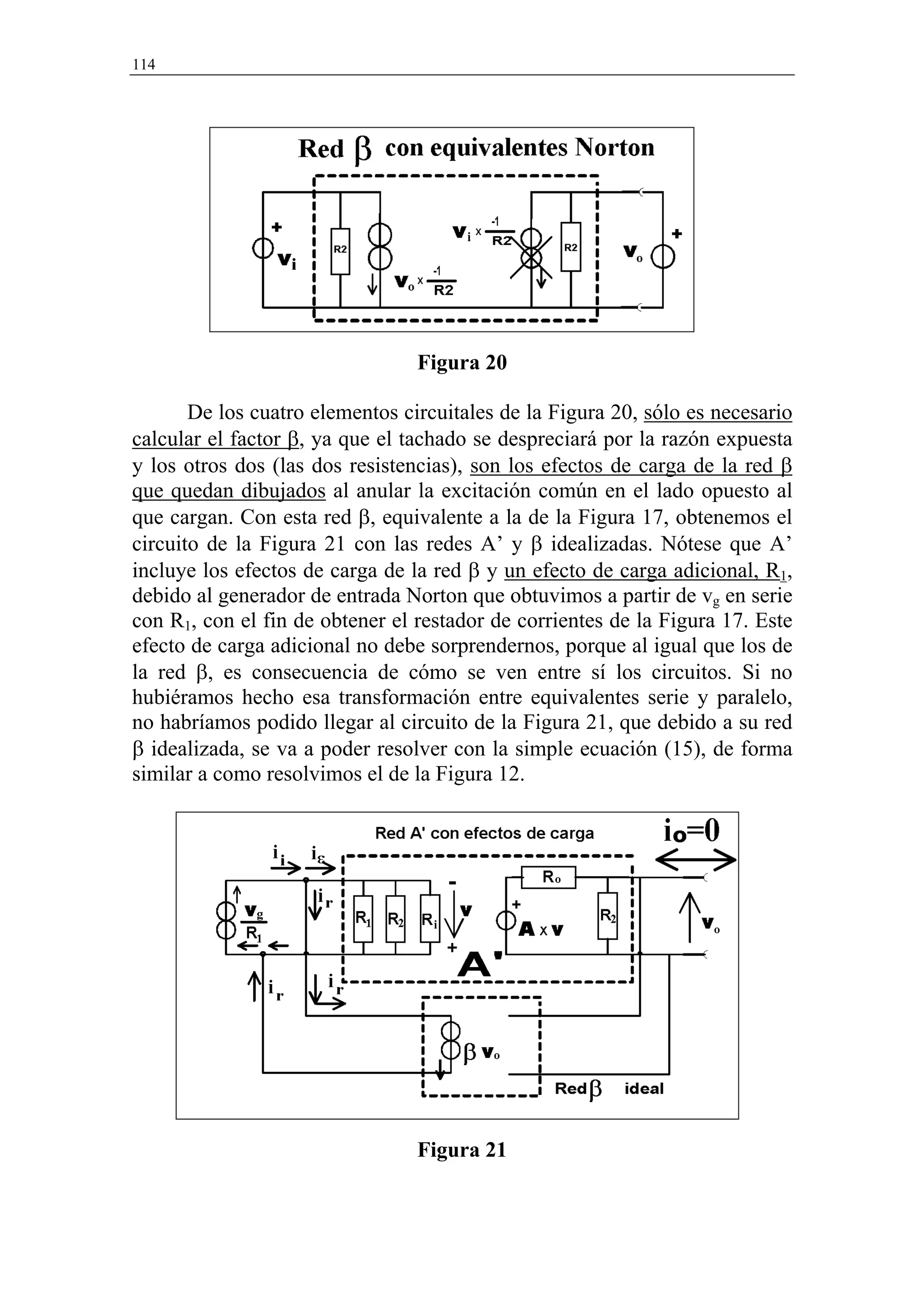
ecuación (11). Por tanto, la conexión paralelo a la salida de las redes A’ y β
hace que la resistencia de salida del circuito realimentado sea la de la red
A’ dividida por el factor (1+A’β). Ello es: RoCR≈Ro/104=0.1Ω.
En resumen: pasando hacia la red A los efectos de carga de la red β
real obtenemos una red A’ y una red β idealizada que funcionan de acuerdo
a la ecuación (15) formalmente idéntica a la ecuación (3) que obtuvimos
para el diagrama de la Figura 2. Debido a ello, las impedancias de entrada y
de salida del circuito total realimentado son las de entrada y salida de la red
A’ multiplicadas o divididas por el factor (1+Aβ) según sea la conexión
(serie o paralelo) de las redes A y β a la entrada y a la salida.
Empleando la ecuación (15) es fácil comprobar con los valores que
venimos manejando que la ganancia del amplificador de la Figura 13, que
antes denominamos Configuración Amplificadora No-Inversora (CANI),
es: G=(1+R2/R1), justo el inverso del factor β de realimentación debido a
que la ganancia de lazo T=A’β=10.000 es mucho mayor que la unidad. El
alto valor de T también es la causa tanto de la alta impedancia de entrada
del circuito total (100GΩ ≈Ri×10.000), como de su baja impedancia de
salida (0,1Ω≈Ro/10.000). De este modo tenemos una visión muy completa
del amplificador global G tanto para su análisis como para su diseño. Este
potente método para resolver el circuito sin necesidad de aplicar ITV(SC)
resulta muy útil y aún va más allá al darnos pautas para elegir los valores
de R1 y R2 a la vista de la Figura 12 y de su ganancia asociada la ecuación
(12), cosa que la aproximación ITV(SC) no hace.
Así valores de R1 y R2 tales que R1+R2 fuese inferior a Ro(∼1KΩ) no
serían adecuados: la salida del AO sufriría y además se perdería ganancia
A’ inútilmente. Valores de R1 muy grandes tampoco serían recomendables
porque si tomásemos R1=1MΩ por ejemplo, entonces R2 sería de 99MΩ.
Su combinación en paralelo será muy próxima a R1 (1MΩ) lo que ya es el
10% de Ri, por lo que el efecto de carga a la entrada se empieza a notar
(perdemos un 10% de ganancia A’ de forma innecesaria) y por otra parte,
una resistencia R2 tan alta (99 MΩ) es muy proclive a ser “puenteada” por
elementos parásitos imprevistos que modificarán el valor de impedancia
que ofrece. Bastarían C=0.5 pF de capacidad parásita en paralelo con R2 (la
de sus propios terminales si no se dejan cortos) para que a la frecuencia de
unos 3 KHz el módulo de la impedancia ofrecida por el circuito R2-C
paralelo así formado, fuese sólo el 70% de 99 MΩ (99/√2 MΩ), cosa que se
reflejaría en la ganancia global G. Tendríamos una RN dependiente de la
frecuencia, lo que a su vez haría depender de la frecuencia el factor
[1+A’β(jω)] y todo aquello que depende del mismo: ganancia G(jω) e
impedancias terminales ZiCR(jω) y ZiCR(jω).](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-109-2048.jpg)























![Diseño con Amplificadores Operacionales 135
Capítulo IV: Diseño de sistemas con AO y
Realimentación Negativa
IV.1- Introducción
En este capítulo veremos la forma de proceder a la hora de diseñar
sistemas formados por varias etapas con AO realimentados negativamente.
Salvo en algunos amplificadores en los que esas etapas quedan conectadas
de forma nativa en serie, es bastante común que se conecten en cascada,
una detrás de otra. En este caso una práctica bastante común es el diseño de
esas etapas por separado y luego conectarlas sin más, esperando que cada
una siga comportándose como si estuviera aislada, sin importar qué tiene
que excitar cada etapa ni qué le está excitando a cada etapa. Esta forma de
proceder es conceptualmente errónea, pero con ideas claras sobre lo que
estamos haciendo, puede resultar válida en la práctica.
Tras presentar esas ideas y sus fundamentos en etapas amplificadoras
diferenciales pasaremos a estudiar el diseño de etapas amplificadoras para
el manejo de señales débiles. Ello nos servirá para ver cómo armonizar los
criterios de diseño del MRA del Capítulo anterior con otros nuevos que
aparecen al querer diseñar etapas que añadan el menor ruido posible a las
débiles señales que tienen que amplificar o procesar.
No haremos una presentación exhaustiva de los muchos subsistemas
(amplificadores, integradores, convertidores I-V y V-I, filtros, sumadores,
etc.) que se pueden hacer con AO realimentados negativamente. Existen
excelentes libros [7], [8] y notas de aplicación de fabricantes de AO [9],
que cubren el tema ampliamente. Nuestra forma de proceder será más bien
la de tomar un cierto sistema o subsistema con AO, analizarlo mediante
ITV(SC) para ver rápidamente su funcionalidad (qué hace o para qué sirve)
y ver a continuación qué condicionantes de diseño nos sugiere el MRA que
vimos en el Capítulo anterior. Este proceso suele ser el más enriquecedor y
nos dará muchas veces ideas nuevas de diseño para nuevos sistemas o
subsistemas. Diremos aquí que serán subsistemas aquellos circuitos con un
solo AO, mientras que sistemas serán aquellos que lleven más de un AO o
más de una realimentación. De esta forma los circuitos analizados en el
Capítulo anterior serían subsistemas en general y a partir de ahora será
cuando empecemos a presentar algunos sistemas.
Con las ideas del párrafo anterior pasaremos a considerar algunos
aspectos relacionados con efectos relacionados con la frecuencia de señales
que varían en el tiempo. Estos efectos no son los “clásicos” sobre respuesta
en frecuencia de circuitos realimentados, sino otros menos tratados en los
libros debidos a efectos de capacidades parásitas inevitables en muchos
sistemas. El intento de reducirlas en algunos casos nos llevará a sistemas](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-135-2048.jpg)










![146
ganancias de los AO, por lo que variaciones del 20% son muy posibles. De
todas formas esa diferencia ya no será de un orden de magnitud o más
como sucedía con el sistema de la Figura 3. Así tendremos un amplificador
diferencial con excelentes propiedades en sus entradas y cuyo CMRR sólo
dependerá de los dos cocientes R4/R3 en cada rama del AO3 en la Figura 5.
El sistema de la Figura 5 es una buena solución como amplificador
diferencial, pero tiene el inconveniente de que toda la ganancia del circuito
la debe proporcionar AO3 y es igual a R4/R3, como puede verse en la
ecuación (10) haciendo R2=0 (y R1→∞ si se desea). Esta situación hace que
a veces el ancho de banda conseguido para una cierta ganancia no sea
suficiente, situación que se deriva del hecho de que muchos AO vienen
compensados internamente mediante lo que se llama ganancia controlada
por un polo dominante. Esa compensación resulta necesaria para evitar que
el AO se vuelva inestable al ser realimentado cada vez más (por ejemplo
con factores β cada vez más cercanos a la unidad). Los motivos de esta
forma de proceder pueden verse en [6, 8, 14] y por ahora lo único que hace
falta saber es que esa compensación da lugar a que el AO posea una figura
de mérito (G×Bw) conocida como producto Ganancia×Ancho de Banda.
Con el tipo de realimentación pasiva que tiene el AO3 de la Figura 5, el
producto G×Bw del AO3 y el del amplificador diferencial construido en
torno al AO3 son similares. De esta forma, si el AO3 posee un producto
G×Bw=5MHz y la realimentación que le aplicamos mediante R3 y R4 le
reducen su ganancia hasta un valor de 100 por ejemplo, la ganancia de 100
se mantendrá hasta la frecuencia ƒc=G×Bw/100=50KHz y a partir de ahí
caerá con la frecuencia. En otras palabras: el producto G×Bw se mantiene
al realimentar negativamente y es posible que el producto GBw del AO3 no
sea suficiente para lo que deseamos en el sistema de la Figura 5.
Por ello sería bueno que las etapas de entrada amplificasen también,
pero sin necesitar ese ajuste tan preciso de sus cocientes R2/R1 que vimos
para el sistema de la Figura 4. Sería mejor aún que esas etapas de entrada
amplificasen mucho la señal diferencial y poco la señal en modo común,
cosa que no ocurre en el circuito de la Figura 4, donde las etapas de entrada
amplifican por igual tanto la tensión común a vA y vB como la diferencial
entre vA y vB. La resta posterior en AO3 de las tensiones en los puntos A y
B es la que cancela las aportaciones debidas a la parte común de vA y vB en
las salidas de AO1 y AO2. Sin embargo, esta situación donde se arrastra y
se va amplificando a lo largo del circuito una componente común, que
suele ser además mucho mayor que la componente diferencial que interesa
amplificar, no es deseable en absoluto y un ejemplo aclarará las cosas.
Supongamos que las entradas del circuito de la Figura 4 se conectan
a sendos electrodos de un equipo de encefalografía (EEG) para recoger y
amplificar una débil señal eléctrica de 10 microvoltios eficaces que aparece
entre ellos (por tanto es señal diferencial: si fuera señal en modo común,](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-146-2048.jpg)




![Diseño con Amplificadores Operacionales 151
Como habíamos propuesto una ganancia 100 para la etapa de salida,
necesitamos una ganancia diferencial de 100 en las etapas de entrada. Por
tanto: 2R2/R11=99 y como el efecto de carga a la salida de AO1 y AO2 es
R2 en serie con R11/2 (R2 en serie con R1 en la Figura 7, porque la tensión
del punto de unión de las resistencias R1 no varía bajo excitación
diferencial: es como si fuera una “masa”), ya podemos elegir R2=99KΩ y
R11=2KΩ como valores razonables por ahora y así obtenemos la Figura 8.
Figura 8
El lector familiarizado con el análisis de redes simétricas reconocerá
aquí una aplicación del Teorema de Bartlett a la entrada simétrica del
circuito de la Figura 7 y quien desee más detalles puede consultar otra
bibliografía más específica como [5].
El circuito final que tendríamos para nuestro amplificador diferencial
con todas las mejoras propuestas sería el de la Figura 8. Este sistema de tres
AO es lo que se conoce como Amplificador de Instrumentación (AI) y
existe como componente integrado, donde las resistencias pueden aparearse
mejor que empleando componentes discretos. Para componentes discretos
recomendaríamos resistencias del 0,1% de tolerancia y a ser posible de las
que vienen encapsuladas en “arrays” de resistencias de precisión. También
es recomendable incluir la posibilidad de un ajuste preciso de una de las
resistencias de la etapa de salida (véase la pequeña resistencia variable en
la Figura 8) a fin de lograr el máximo CMRR.](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-151-2048.jpg)
![152
IV.3- Ruido en Amplificadores Operacionales
El ruido en componentes electrónicos y en los sistemas basados en
ellos que construyamos, es algo inevitable e incluso diremos que inherente
a la naturaleza de los mismos. Así el ruido de origen térmico resulta como
consecuencia del equilibrio termodinámico del componente con el universo
que le rodea y que se encuentra a cierta temperatura absoluta T. Por ello
podemos reducirlo mucho enfriando los componentes hasta temperaturas
muy bajas, pero nunca eliminarlo del todo. Más aún: en bastantes casos no
resulta posible llevar a cabo ese enfriamiento y en muchos más ni siquiera
hace falta. Lo que sí suele buscarse es el diseño de amplificadores para
manejar señales débiles con cierto ruido añadido, que amplifiquen esa señal
y ese ruido sin añadir apenas más ruido extra. Es decir: deben amplificar la
señal de entrada que les llega sin degradar mucho la relación señal/ruido de
entrada (S/N)i que trataremos de preservar a fin de que la nueva relación
señal/ruido a la salida (S/N)o no sea mucho peor que la (S/N)i. Veremos
que con cierto cuidado al elegir los componentes (AO, resistencias, etc), es
posible no tener degradaciones importantes de la relación S/N, o al menos
tener la menor posible para una fuente de señal dada.
Antes de ver cómo va a degradar la relación (S/N) una etapa
amplificadora con AO conviene tener claros algunos conceptos sobre ruido
y fuentes de señal. Por una mayor simplicidad y claridad en la exposición
que viene, supondremos fuentes de ruido térmico cuyo espectro en potencia
es plano con la frecuencia. Ello permite trabajar con valores de densidad
espectral de ruido o con potencias de ruido en un ancho de banda de 1Hz en
torno a una frecuencia dada (“spot noise”) y considerar después el ancho de
banda del sistema para obtener la potencia total de ruido. Esto supone un
tratamiento bastante básico en cuanto al tipo de ruido presente en nuestros
circuitos y sistemas, pero el lector interesado en el tema puede consultar
obras específicas mucho más amplias como [10].
Nuestro punto de partida será que una resistencia R a la temperatura
absoluta T presenta una pequeña fluctuación de tensión entre sus extremos
dejados “al aire” o una pequeña fluctuación de corriente entre sus extremos
cortocircuitados. El valor medio de esas fluctuaciones es cero, pero no así
el valor eficaz de las mismas, y podemos decir que se deben a la agitación
térmica de los portadores de carga que hay en su interior [11, 12]. Ese valor
eficaz depende del ancho de banda (Bw) que tenga el sistema de medida,
de modo que recogiendo todas las aportaciones entre 10 y 1010Hz de ese
ruido, se obtiene cierto valor eficaz y si se recogen las aportaciones entre
10Hz y 100.010Hz se obtendrá un valor eficaz 10 veces mayor. Por lo
tanto, el valor medio de los cuadrados de los valores de tensión medidos a
lo largo del tiempo (valor cuadrático medio vn2) resulta ser proporcional al
ancho de banda. La ecuación que los relaciona es:](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-152-2048.jpg)






![160
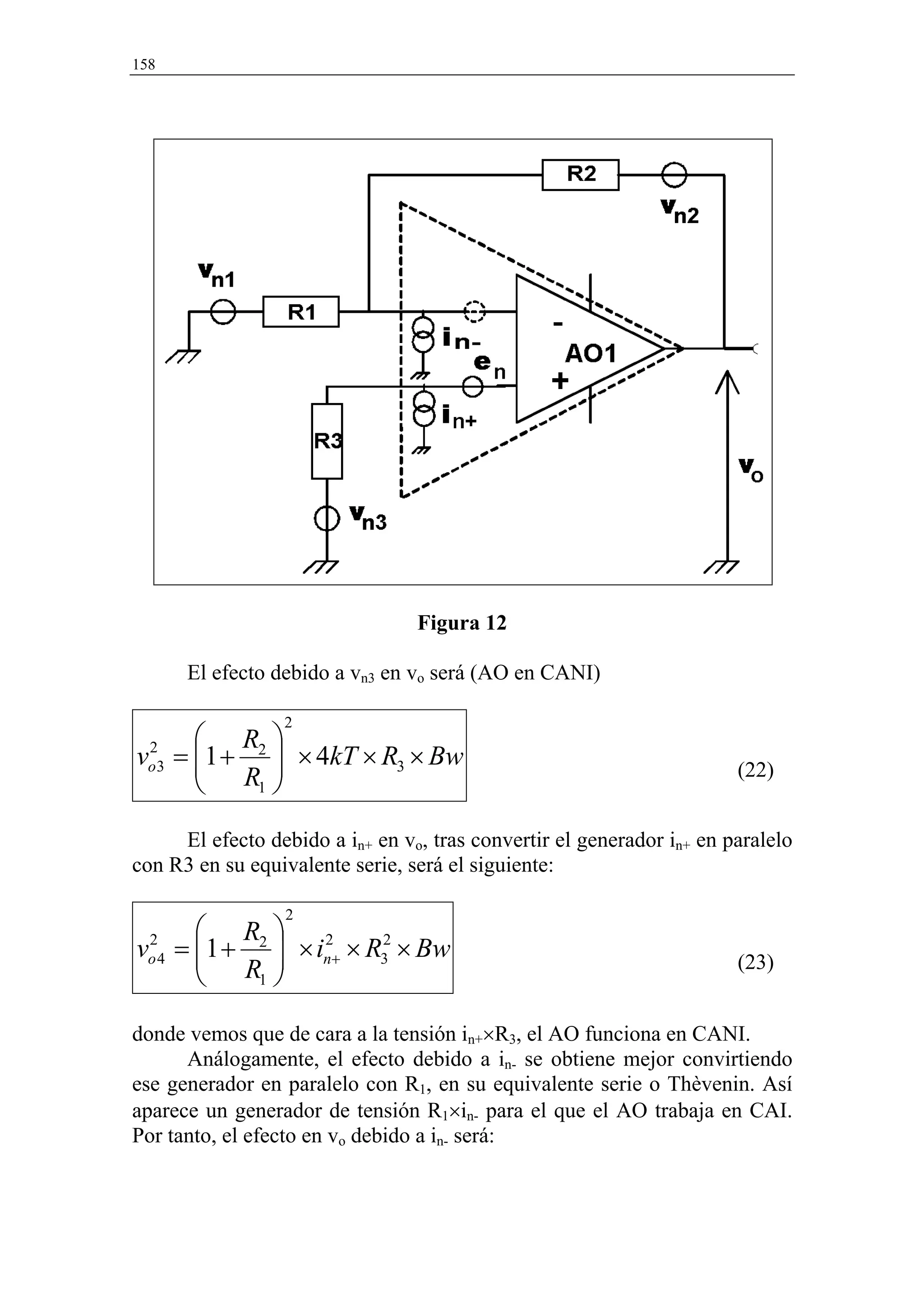
tensión en el punto de unión de R2 y vn2 sea cero. Ello hará que la corriente
por R2 sea nula y nula también la corriente a través de R1 lo que garantizará
que la tensión en la entrada (-) sea igual a la de la entrada (+) que es nula.
Por tanto el efecto en vo debido a vn2 será:
vo 2 = 4kT × R2 × Bw
2
(26)
Antes de sumar las seis contribuciones contenidas en las ecuaciones
(21) a (26) hay que hacer una aclaración respecto a los generadores de
ruido del AO. Lo normal es encontrar equivalentes en e in en los libros que
son densidades espectrales de tensión o de corriente eficaz de ruido
respectivamente. No son por tanto voltios eficaces o amperios eficaces,
sino valores eficaces divididos por la raíz cuadrada de Hz. De esa forma al
elevarlos al cuadrado dan voltios o amperios eficaces al cuadrado divididos
por hercio y al multiplicarlos por los Hz del ancho de banda considerado ya
quedan con dimensiones de V2 o A2, como ocurre con los factores 4KTR o
4KT/R de la ecuación (15) al multiplicarlos por el término Bw. Por ello, las
ecuaciones (23), (24) y (25) están multiplicadas por el factor Bw para ser
valores eficaces de tensión de ruido elevados al cuadrado como lo son las
restantes contribuciones de las ecuaciones (21), (22) y (26).
Sumando las seis contribuciones obtenemos el siguiente ruido total a
la salida (valor cuadrático medio, porque al ser ruido, el valor cuadrático de
tensión de salida no es constante y fluctúa en torno a su valor medio von2):
2
R
R
2
[
von ≈ 1 + 2 × en + in × RN + 4kTRN × Bw
2 2 2
] (27)
1
La ecuación (27) no es estrictamente la suma exacta, pero es la que
se utiliza para el diseño por ser fácil de recordar. Las aproximaciones que
se han hecho para su obtención son dos bastante razonables. La primera
aproximación supone: in-=in+=in (bastante cierta en la mayoría de los casos)
y se refleja en que los fabricantes de AO sólo suelen dar una in (medida en
A/√Hz) y la en medida en V/√Hz. La segunda aproximación supone que:
in × R32 + ( R1 R2 ) 2 ×in ≈ in × ( R3 + R1 R2 ) 2 =in × RN
2 2 2 2 2
(28)
y se hace con el propósito de obtener una ecuación (27) que sea fácil de
recordar y aplicar como veremos enseguida. Antes hay que resaltar que la
Resistencia Total de Ruido RN viene dada por:](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-160-2048.jpg)


![Diseño con Amplificadores Operacionales 163
La Figura 14 presenta el circuito propuesto en el que se asume que la
corriente de polarización IB+ de la entrada (+) del AO circula a través del
propio sensor, cosa que dicho sensor debe permitir. Esto puede ser así en
captadores electrodinámicos, donde la bobina de hilo conductor que detecta
variaciones de flujo magnético suele permitir el paso de IB+ sin problemas.
Figura 14
Otra cosa sería un sensor piezoeléctrico por ejemplo, para el que
habría que modificar algo la entrada a fin de permitir el paso de IB+. No
vamos a entrar en detalles sobre este caso, pero hacemos ver la importancia
de que IB+ pueda circular: si no puede hacerlo, no existe el AO y menos aún
el amplificador propuesto. En este caso una resistencia entre la entrada (+)
y masa soluciona el problema si se puede elegir de modo que no forme
atenuador apreciable con la resistencia de salida del sensor.
Volviendo a la Figura 14, el condensador CA va a limitar el ancho de
banda en la parte de altas frecuencias a 1KHz y se diseña haciendo que a
1KHz su reactancia sea igual a la resistencia R2. Así el circuito presentará
un filtrado paso-bajo de primer orden con una frecuencia de corte superior
de 1KHz, que para potencia de ruido supone un Bw=(π/2)×1KHz [10]. El
condensador CB tiene la misión de limitar el ancho de banda en la parte de
bajas frecuencias a 100Hz y se diseña haciendo que su reactancia a 100 Hz
iguale a la suma de las resistencias que debe acoplar. Esas resistencias son
los 50KΩ de la etapa siguiente y la resistencia de salida del propio AO
realimentado que será del orden del ohmio si cuidamos el factor A’β del
circuito como permite hacerlo el MRA del capítulo anterior. Nótese que en
esa resistencia de salida debió intervenir la propia resistencia de 50KΩ en
serie con CB, porque según el MRA, todo lo que haya en la salida debe ser
incluido ya que afecta al producto A’β. En nuestro caso, su efecto es escaso](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-163-2048.jpg)



![Diseño con Amplificadores Operacionales 167
distintos. Luego se suman las salidas de esas N etapas y lo que es señal se
sumará en tensión mientras que los ruidos de las N etapas se sumarán en
potencia (es decir cuadráticamente). Con ello se logra reducir en un factor
√N el equivalente de ruido en tensión en del AO presente en las N etapas de
entrada a costa de aumentar en ese mismo factor el equivalente de ruido en
corriente in global. Con ello la nueva RoptN que resulta es:
en
RoptN = N = Ropt
N × in N (36)
Esta es la propuesta que aparece en la Figura 16, tomada del catálogo
de Linear Technology [15], que emplea el AO de muy bajo ruido LT-1028,
con equivalentes de ruido en=1nV/√Hz e in=1pA/√Hz, de los que se deduce
una Ropt=1KΩ. Haciendo n=5 en el circuito de la Figura 16, tendríamos un
sistema amplificador de bajo ruido para una fuente de señal de 200Ω de
resistencia de salida, que es bastante baja y plantea problemas con diseños
basados en un solo AO, aunque éste sea de los mejores existentes para bajo
ruido. Animamos al lector a demostrar la ecuación (36) para el circuito de
la Figura 16, porque es un excelente ejercicio de sumas (superposición más
bien) de señales, unas veces en tensión y otras en potencia, que ayudan a
educar el “sentido común” en esta temática de ruido electrónico. Como
ejemplo del modo de proceder, considérese que la corriente de ruido del
AO número “i” de los N de entrada, al circular por la resistencia de la
fuente de señal, generará una tensión de ruido que será “vista” por los N
amplificadores, por lo que sus salidas se sumarán en tensión . Sin embargo,
las aportaciones de este tipo debidas a los AO número “i” y número “j”
(hasta recorrer todo N) se sumarán en potencia, porque en principio la
generación interna de ruido en cada AO no tiene relación con la generación
de ruido en los restantes y por tanto esos ruidos estarán incorrelados.
El bajo valor de 470Ω en los AO de entrada de la Figura 16 requiere
cierta explicación. Ello se puede hacer sin estropear apenas el producto A’β
porque la Ro del AO LT-1028 es de unos 80 ohmios y no de 1KΩ como
valor típico que venimos asumiendo. Es éste un AO un tanto especial, de
reducidísimo ruido en conseguido por las altas corrientes de los transistores
del par diferencial de su entrada y que debido a ello posee una “baja” Ri de
sólo unos 20KΩ. Su ganancia Ad es del orden de 30×106, bastante más alta
que el valor típico de 106 que venimos empleando y debido a las altas
corrientes de polarización de su par diferencial de entrada, su equivalente
de ruido en corriente es algo mayor que en los AO con tecnología bipolar.](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-167-2048.jpg)
![168
Figura 16
Un último consejo relacionado con diseño para bajo ruido se refiere a
la necesidad de acoplar bien a “masa”, a efectos de variaciones de tensión,
los terminales +Vcc y –Vcc de los AO empleados. Así, dos condensadores
electrolíticos de un valor comprendido entre 10 y 100µF, conectados entre
cada uno de esos terminales y masa, suelen resolver la mayoría de los
problemas relacionados con bajas frecuencias. Para los relacionados con
altas frecuencias, en las que esos condensadores electrolíticos ya no
responden bien, un condensador cerámico de valor comprendido entre 10 y
100 nF, conectado en paralelo con cada electrolítico, resultará muy eficaz.
La eficacia de estos condensadores es tanto mayor cuanto más cerca se
pongan físicamente de las patillas +VCC y-VCC del AO. Si se colocan lejos
de ellas, la longitud de las pistas de circuito impreso que los unen al AO
puede dar lugar a la aparición de cierta inductancia parásita. Ello unido a la
propia resistencia óhmica de la pista, hace que los condensadores no
puedan mantener constante las tensiones +VCC y-VCC del AO cuando éste
varía la corriente que pide o da a dichos terminales, según se lo exigen las
señales que está manejando. Lo anteriormente expuesto es lo más básico de
un tema muy amplio y complejo a veces, que es la reducción de ruido en
sistemas electrónicos. Remitimos al lector interesado a referencias como
[16] y [17] donde encontrará más información sobre el tema.](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-168-2048.jpg)
![Diseño con Amplificadores Operacionales 169
IV.5- Consideraciones iniciales sobre efectos de la frecuencia
Como el lector habrá podido comprobar, hemos pretendido resaltar
los efectos debidos a la realimentación negativa, considerando redes A y β
resistivas en general, es decir, sin efectos con la frecuencia. Ello hacía que
los valores de las ganancias A’ y β fuesen constantes, permitiendo apreciar
claramente los efectos del factor (1+A’β) tanto en la ganancia global G
(reducción y desensibilización por dicho factor) como en las impedancias
terminales de la red total G a la que equivalen las redes A y β conectadas
según alguna de las cuatro topologías que se han visto (modificación de
impedancias de la red A’ por dicho factor). Estas ideas permanecen aunque
aparezcan elementos reactivos (condensadores y bobinas) en los diseños
que den lugar a ganancias A’(jω) y β(jω) que varíen con la frecuencia.
Vamos ahora a dar una panorámica reducida pero ilustrativa del gran
campo que se abre al considerar simultaneamente realimentación negativa
y efectos con la frecuencia. Aspectos sobre el comportamiento con la
frecuencia de sistemas y circuitos realimentados aparecen en varias de las
referencias de la bibliografía [2], [4], [6], [8] a las que remitimos al lector
interesado en estos temas. Nuestro objetivo aquí va a ser más bien despertar
su curiosidad sobre este interesante tema con unos ejemplos basados en lo
visto hasta ahora, que muchas veces no son tratados en esas referencias,
aunque la teoría allí expuesta les sea aplicable. Serán ejemplos simples,
pero reales y por tanto útiles para educar el “sentido común electrónico”
del lector en estos temas. Los iremos presentando como casos de estudio a
los que aplicaremos lo visto hasta ahora.
Caso I.- Efecto de la capacidad parásita de entrada del amplificador.
Supongamos que tenemos un sensor o fuente de señal de alta
impedancia (10MΩ por ejemplo) cuya señal deseamos amplificar por un
factor 1000 en tensión (60 dB). Asimismo deseamos que el amplificador
que diseñemos apenas cargue a ese sensor, por lo que su impedancia de
entrada nos interesa lo más alta posible, por encima de 1012Ω si es posible.
Por otra parte queremos que esa amplificación sea con bajo ruido, lo que
nos sugiere que el AO que elijamos tenga su par diferencial de entrada con
tecnología FET. De nos ser así el ruido en corriente del AO a su entrada se
convertirá en un gran ruido en tensión sobre la alta resistencia del sensor
(que hará el papel de R3 en la Figura 11). Debido a esto, el impresionante
AO LT-1028 de la Figura 16 aquí no sirve, porque su in=1pA/√Hz sobre los
10MΩ se convierte en nada menos que 10µV/√Hz que dan una Figura de
ruido de varios centenares según la ecuación (34). Aquí nos viene mucho](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-169-2048.jpg)


![172
central del cable coaxial y la malla intermedia, respecto al formado por esa
malla y la malla exterior de blindaje electrostático.
Figura 18
Nótese en la Figura 18 que sólo hay una conexión “a masa” de la
malla exterior del cable triaxial en el lado del amplificador. Obsérvese
también que la malla intermedia está a un potencial que es el 90% del que
tenga el hilo central del cable triaxial debido al divisor de las resistencias
de 9Ω y 1Ω. Esto hace que el condensador coaxial cilíndrico existente entre
el hilo central y la malla intermedia, sea 10 veces menos efectivo que si esa
malla estuviera conectada al potencial de masa. Esta forma de proceder
pertenece al tipo de técnicas de guarda y “bootstrapping” que pueden
encontrarse en diversas referencias [18], [19] a las que remitimos al lector
interesado. Aquí solo diremos que bajo el punto de vista de realimentación,
la acción anterior conlleva la aparición de cierta realimentación desde la
salida del AO hacia su entrada (+) a través de la capacidad existente entre
el hilo central y la malla intermedia (condensador cilíndrico Cint). Esta es
una realimentación positiva que origina un circuito que tiene dos tipos de
realimentación (negativa y positiva), cuyas propiedades y comportamiento
no son ni evidentes ni tan sencillos de ver como los de circuitos con sólo
realimentación negativa. Este tema de la doble realimentación requiere
cierto sentido común electronico y será tratado en el último capítulo del
libro, por lo que concluiremos por ahora con la Figura 19 que muestra el
circuito al que equivale en primera aproximación el sistema sensor-
amplificador de la Figura 18. Nótese que Cext es el condensador cilíndrico
debido a la capacidad entre las mallas intermedia y exterior del cable
apantallado triaxial.](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-172-2048.jpg)


![Diseño con Amplificadores Operacionales 177
saturado y en ese caso hay que descargar de alguna forma el condensador
(mediante un interruptor o una resistencia en paralelo con C) en la que no
vamos a entrar ahora.
Figura 23
Quedémonos con la idea de que el circuito es un buen integrador
para señales que no tengan componente continua ni sean de muy bajas
frecuencias y como ejemplo de la potencia del MRA que hemos visto, que
sirve también para cuando las funciones A’ y β dependen de la frecuencia,
vamos a mostrar cómo será la impedancia de salida del integrador de la
Figura 20. Debido a la RN esperamos una ZoCR que sea muy baja porque
será la ZoSR de la red A’ dividida por el factor [1+A’β(jω)] dada la
conexión paralelo de las redes A’ y β a la salida, pero nótese que ahora el
producto A’β depende de la frecuencia. La red A’ que obtendríamos
empleando el MRA sería la que se representa en la Figura 24.
Figura 24](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-177-2048.jpg)




![182
de amplificadores basados en AO para fotodiodos, podrá encontrar mucha
más información en la referencia [20].
Figura 28
Con los valores de la Figura 28, el efecto de carga (dentro de la red
β) de los 5MΩ sobre el atenuador por 20 (resistencias de 50KΩ y 950KΩ)
es despreciable. En otras palabras, la tensión vo queda dividida por 20 antes
de ser aplicada a la resistencia de 5MΩ que realimentará una corriente ir
hacia la entrada, proporcional por tanto a vo/20. Esta visión del convertidor
I-V de la Figura 28 resulta mucho más instructiva que la simple resolución
de dicho circuito mediante la aproximación ITV(SC), que el lector puede
hacer como ejercicio práctico sabiendo ya “lo que tiene que obtener”.
IV.6- Realimentaciones negativas no-lineales y ocasionales
En los apartados anteriores hemos ido viendo diversos sistemas que
se obtenían al aplicar realimentación negativa a un AO mediante una red β
formada por elementos lineales, que para nosotros serán aquellos elementos
circuitales (resistencias, capacidades e inductancias) cuyo valor no depende
de la amplitud de las señales que existan sobre dichos elementos. Así una
resistencia de valor R presenta una característica corriente-tensión (I-V)
que decimos que es lineal porque si dibujamos una gráfica de la corriente I
que atraviesa R en función de la tensión V que hay entre los extremos de R,
aparece una línea recta de pendiente 1/R (función lineal) en todo el rango
de valores de tensión V que manejamos en Electrónica (sean nV, µV, mV,
voltios, etc). El empleo de elementos lineales en la red β bajo RN da lugar
a que las funciones de transferencia obtenidas (GV, GI, GZ y GY) también
sean funciones lineales o valores constantes independientes tanto de la
amplitud como del signo de las señales que estén manejando.](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-182-2048.jpg)



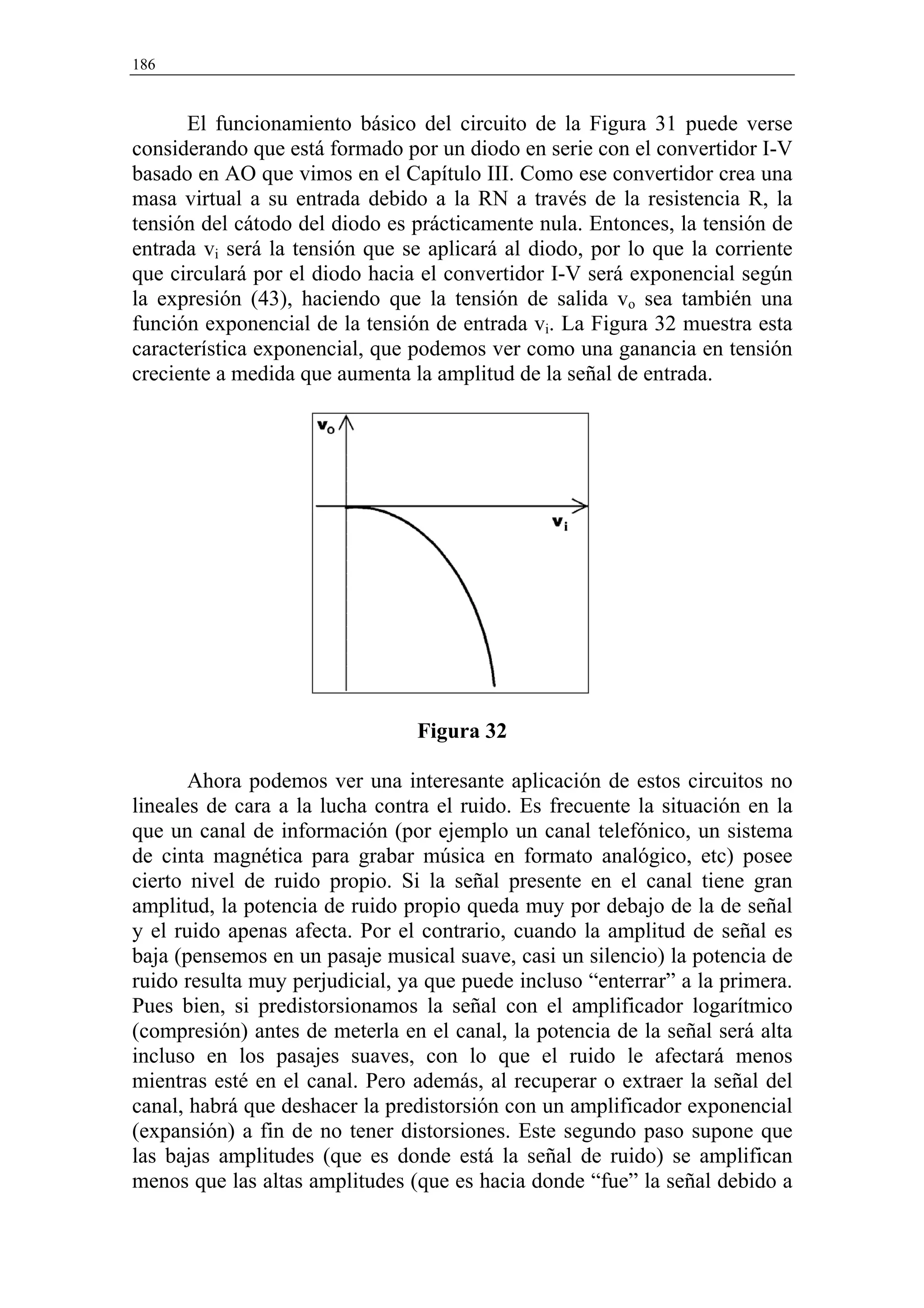
![Diseño con Amplificadores Operacionales 187
la predistorsión). De esta forma se reduce el ruido de forma notable gracias
al empleo de un sistema “compansor” (compresor-expansor) similar a este
ejemplo básico con amplificadores logarítmicos y exponenciales.
Otras aplicaciones de estos circuitos y de sus versiones comerciales
mejoradas conciernen al tratamiento analógico de señales electrónicas. Si
una tensión analógica vi(t) se procesa con un amplificador logarítmico y la
salida de éste se amplifica por 3 linealmente, la señal resultante puede
hacerse pasar o procesarse con el amplificador exponencial inverso del
primero para obtener la señal analógica vi(t) elevada al cubo en virtud de la
expresión (44).
exp(3× Ln[vi (t )]) = (exp(Ln[vi (t )])) = (vi (t ))
3 3
(44)
Si en vez de la amplificación lineal por 3 hubiésemos atenuado por 2
la señal de salida del logarítmico, lo obtenido a la salida del exponencial
sería la raíz cuadrada de vi(t). Nótese que si deseásemos emplear los
circuitos de las Figuras 29 y 31 para hacer el cálculo anterior, uno de los
diodos de esos circuitos debería invertirse (por ejemplo el de la Figura 31)
para que el signo de la tensión de salida del amplificador logarítmico y el
de la señal de entrada del exponencial fuesen compatibles. Lo anterior da
una idea de las posibles aplicaciones de este tipo de circuitos en cuanto a
cálculo analógico, del que el cálculo de valores eficaces y potencias de
señales sería un buen ejemplo. Remitimos al lector interesado a referencias
como [7, 8, 14 y 21], donde encontrará un buen número de aplicaciones.
Con este tipo de circuitos no lineales, los conceptos de ganancia y de
impedancia no sirven, salvo que se definan en un cierto entorno, debido a la
gran distorsión que producen, lo que genera señales que no estaban en la
señal inicial. Si atacamos el amplificador de la Figura 29 con una señal
senoidal de 100 mV de amplitud por ejemplo, las partes negativas de esa
señal generarían una tensión de salida positiva muy alta (la máxima que
pudiera dar el AO a su salida) y las partes positivas se procesarían como
hemos visto, con una ganancia logarítmica. Esa señal de salida tan extraña
es toda una suma de señales senoidales de frecuencias múltiplos de la de
entrada (Serie de Fourier). Por tanto, además de a la frecuencia de entrada
(fundamental) se han generado señales a otras frecuencias para las que no
podemos definir una “ganancia” porque no se encontraban a la entrada.
Tampoco podríamos definir una impedancia de salida en el circuito de la
Figura 29 porque al atacar su salida con cierta fluctuación senoidal de
corriente i(t), la fluctuación de tensión v(t) que obtendríamos no sería
senoidal y no podríamos aplicar la Ley de Ohm generalizada para señales
senoidales.](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-187-2048.jpg)


![190
de salida ha de hacerse con cierto cuidado. Así cuando vi sea negativa, el
AO1 hará aparecer en el punto A la tensión de entrada negativa que va
siguiendo debido a que tiene RN a través de su diodo, por lo que crea
ITV(SC) entre sus entradas. En estas condiciones el AO2 no tiene RN, por
lo que la resistencia de 5KΩ entre el punto B y masa tendrá en paralelo
hacia masa la alta impedancia que se “vea” hacia la entrada (-) del AO2,
que por otra parte carece de posibilidad de dar o absorber corrientes
apreciables sobre los 5KΩ. Por ello podemos considerar que la tensión en
el punto B es nula y que entre ese punto y masa sólo está la resistencia. En
estas condiciones, el AO3 y sus resistencias asociadas son un amplificador
con AO en CAI de ganancia unitaria para la tensión del punto A, lo que
hace que en la salida vo aparezca la tensión del punto A invertida, es decir:
la tensión negativa de entrada vi cambiada de signo, o para quien prefiera el
proceso analógico de señales, el valor absoluto de vi.
Por otra parte, cuando vi sea positiva, el AO2 hará aparecer en el
punto B la tensión de entrada tal como es, ya que la va siguiendo debido a
que tiene RN a través de su diodo, por lo que crea ITV(SC) entre sus
entradas. Como en estas condiciones el AO1 no tiene RN, la resistencia de
5KΩ entre el punto A y masa tendrá en paralelo la alta impedancia que se
“vea” hacia la entrada (-) del AO1, entrada que no puede dar ni absorber
corrientes apreciables sobre los 5KΩ. Por ello podemos considerar que
entre el punto A y masa sólo está la resistencia de 5KΩ. En estas
condiciones AO3 y sus resistencias asociadas son un amplificador en CANI
de ganancia 5/3: 1+[10K/(10K+5K)] para la tensión de su entrada (+), por
lo que atenuando la tensión del punto B por un factor 3/5, la salida vo será
la tensión del punto B sin invertir, es decir: la tensión positiva de entrada vi
sin cambio de signo, o pensando en el procesado analógico de señales, el
valor absoluto de vi. De esta forma funciona el rectificador de precisión y
onda completa de la Figura 34, al que también se le puede dotar de
ganancia en tensión diseñando adecuadamente el diferencial de salida.
IV.7- Conclusiones
En este Capítulo nos hemos centrado en el diseño de sistemas con
varios AO que emplean realimentación negativa lineal, lo que nos ha
permitido presentar progresivamente la amplificación diferencial partiendo
de la amplificación “referida a masa” y luego el diseño para obtener
prestaciones de bajo ruido en amplificadores basados en AO. Después y sin
entrar en el tema específico de la respuesta en frecuencia de circuitos
realimentados, hemos presentado algunos efectos básicos con la frecuencia
que aparecen a la entrada y salida de sistemas con realimentación negativa
o en la propia red de realimentación. Algunos como las capacidades de
entrada parásitas, resultan perjudiciales porque reducen el ancho de banda](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-190-2048.jpg)





![196
evoluciona la carga almacenada por el condensador (y por tanto su tensión:
∆v(t)=∆Q(t)/C) tras una variación brusca de las condiciones de excitación.
Estaremos estudiando el caso particular del régimen transitorio del circuito
R-C, una respuesta en el dominio del tiempo íntimamente ligada a su
respuesta en frecuencia, como el lector puede conocer y si no es el caso
consultar, en otros textos [2], [4]. De todos modos, el tratamiento que
haremos aquí no usará el potente método de transformadas de Laplace y
variable compleja s, sino una ecuación temporal básica del circuito R-C
serie o paralelo que permite resolver muchos casos prácticos.
Para empezar con el tema, en la Figura 1 se han dibujado los filtros o
circuitos R-C paso-bajo y paso-alto más simples (de 1er orden) que hemos
mencionado. Como puede verse, la señal de salida en el paso-bajo es la
tensión sobre el condensador, mientras que la señal de salida en el paso-alto
es la que aparece sobre la resistencia. Sin embargo, ambos circuitos tienen
una esencia común que es su evolución temporal a partir de un mismo
estado de carga inicial del condensador. Si de algún modo cargásemos el
condensador de ambos circuitos con la tensión inicial VI=10V por ejemplo,
y anulásemos a continuación la excitación de entrada vi poniendo un
cortocircuito en lugar de ese generador, veríamos que ambos circuitos
evolucionarían de forma similar. Esa evolución sería la descarga de un
condensador C a través de una resistencia R, que iría reduciendo los 10V
iniciales hasta una tensión final de cero voltios (VF=0V).
Figura 1
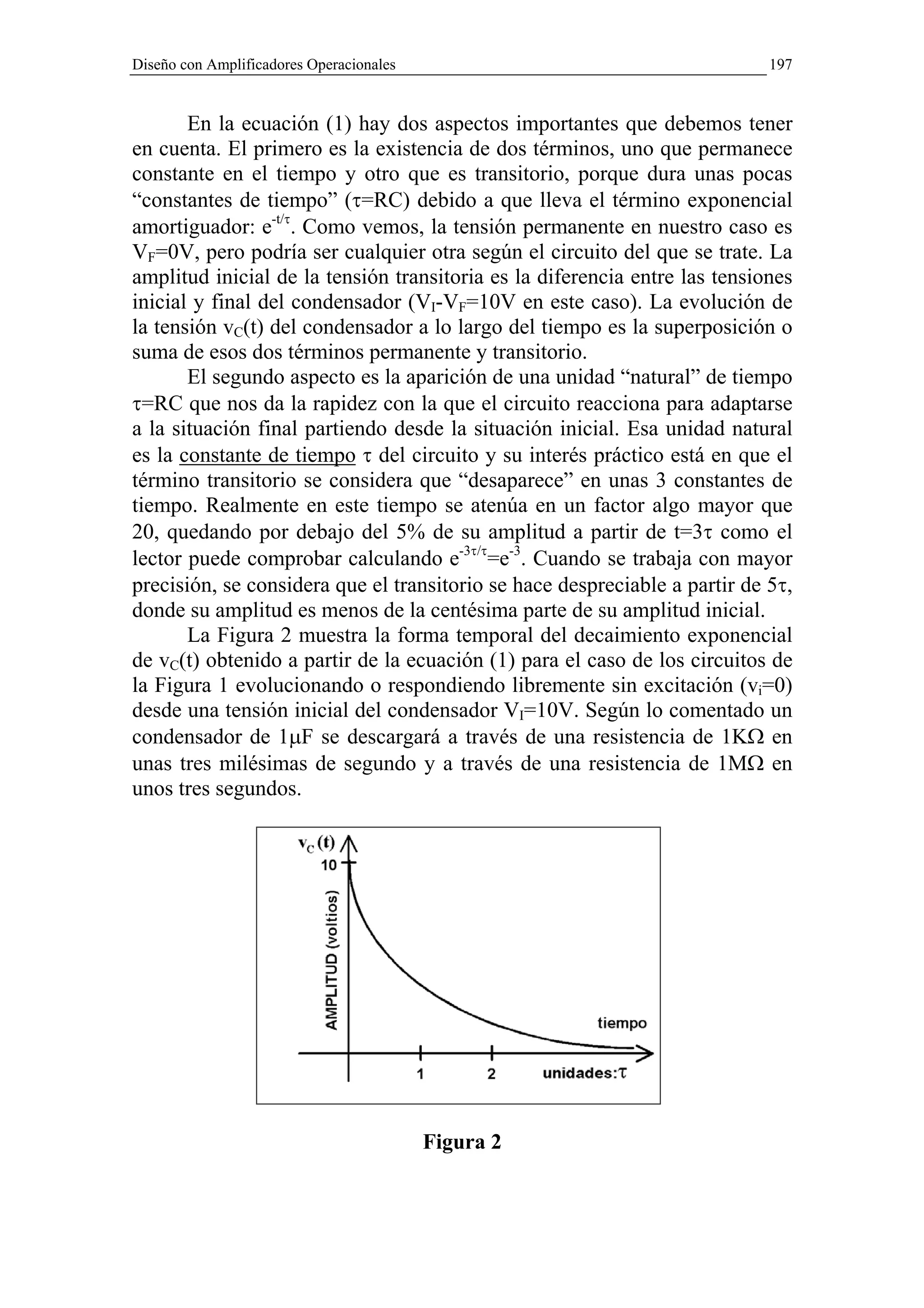
La forma de onda de la tensión del condensador vC(t) en el caso
anterior es un decaimiento exponencial en el tiempo que comienza en VI y
termina en VF (cero voltios en este caso). La ecuación correspondiente es la
siguiente:
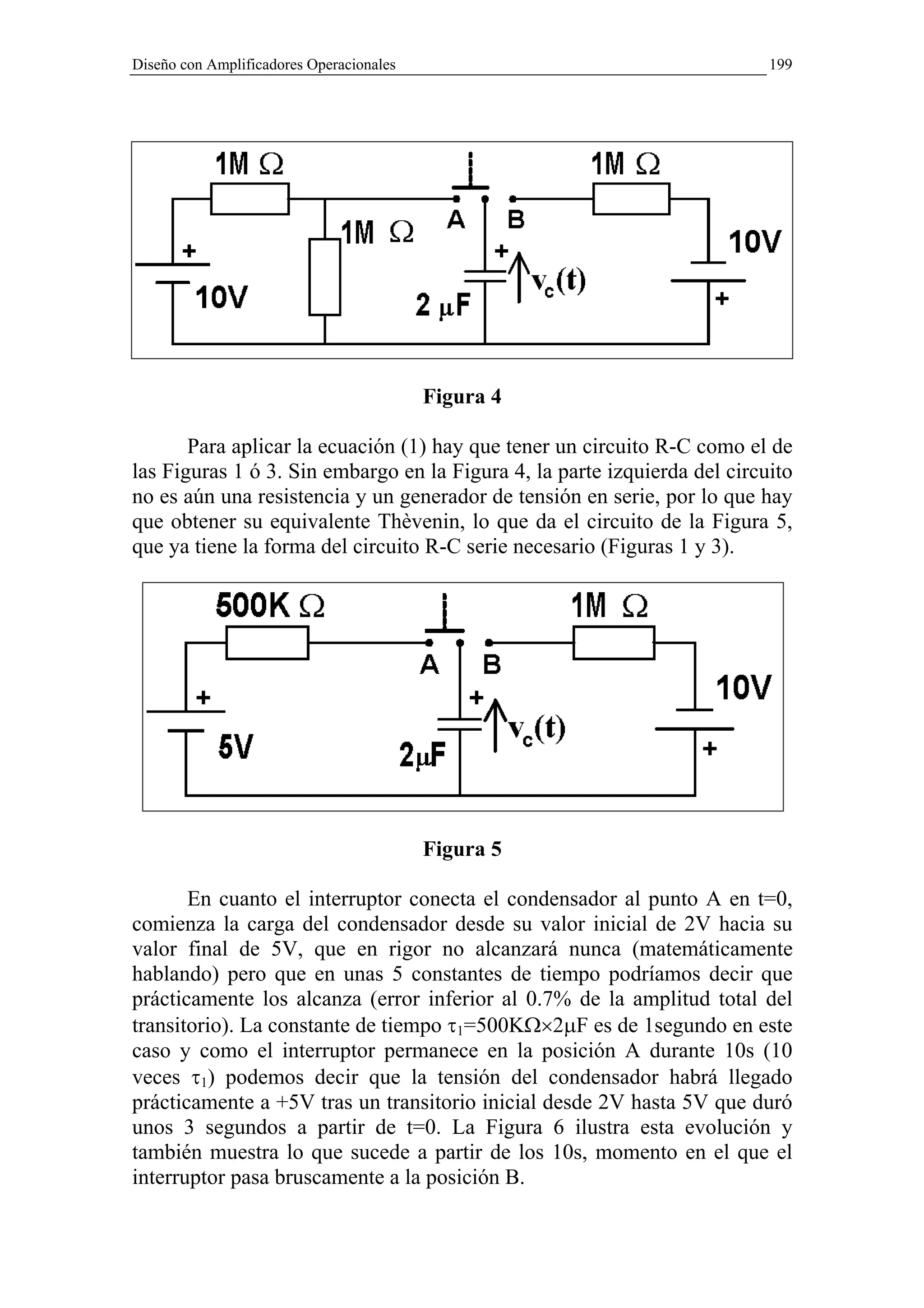
vC (t ) = VF + (VI − VF ) × e ( −t / RC ) (1)](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-196-2048.jpg)

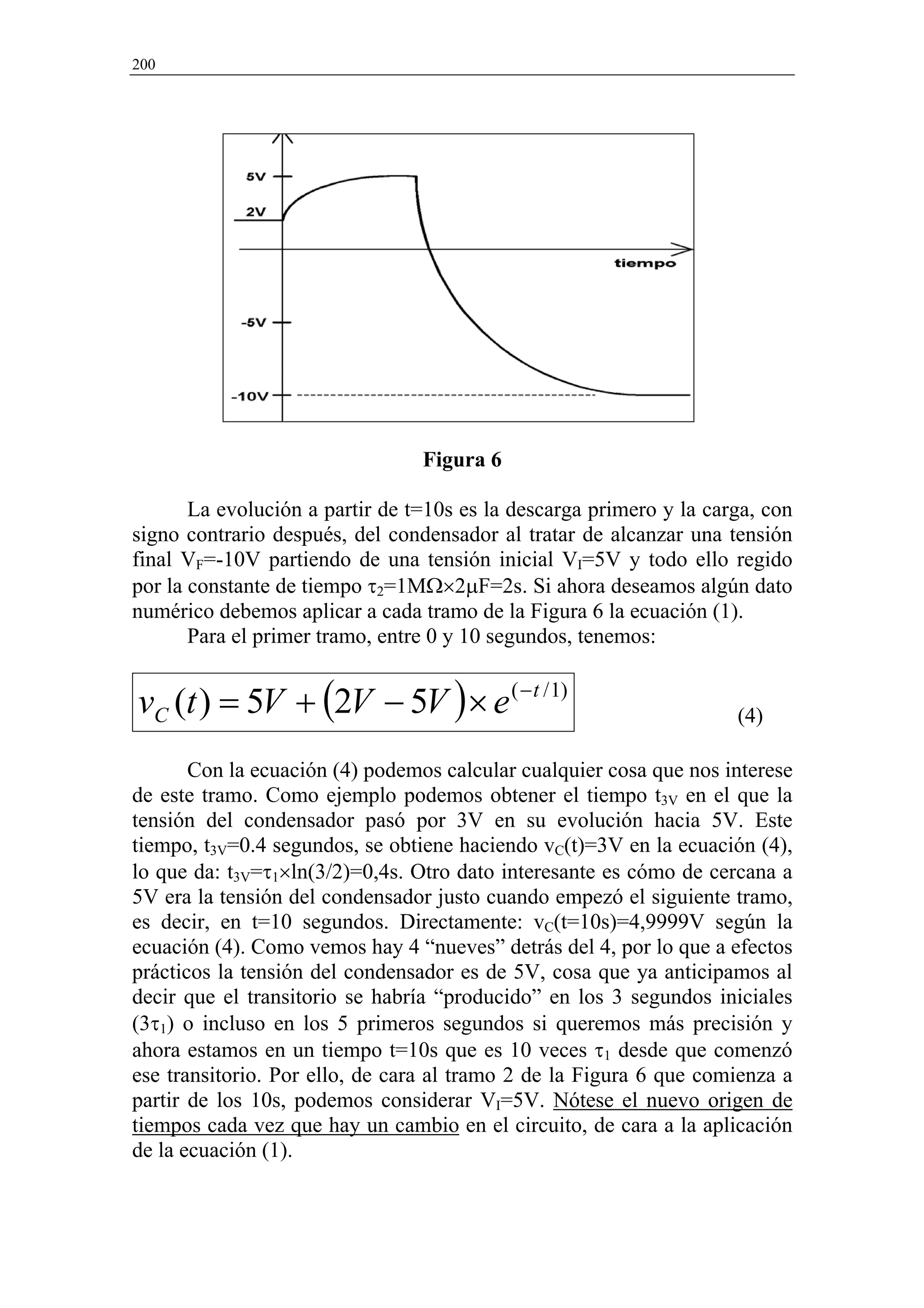
![Diseño con Amplificadores Operacionales 201
Para el segundo tramo, con el nuevo origen de tiempos (t=0) a partir
de los 10 segundos, tendremos:
vC (t ) = −10V + [5V − ( −10V )]× e ( − t / 2 ) (5)
Con la ecuación (5) y considerando el nuevo origen de tiempos
indicado, es fácil ver que el tiempo transcurrido desde que empezó este
nuevo tramo hasta que la tensión en el condensador pasó por cero voltios,
fue de 0,8s: τ2×ln(15/10). Vista la forma de calcular la evolución temporal
de vC(t) en el circuito R-C serie básico, pasamos al estudio del comparador,
báscula o “trigger” de Schmitt que ya vimos en el Capítulo II y al que irá
ligado el empleo práctico de esa evolución del circuito R-C para el diseño
de circuitos monoestables y aestables básicos con AO.
V.3- Biestable básico: Trigger de Schmitt
En la Figura 7 se representa el biestable básico obtenido con un AO
y realimentación positiva que vimos en el Capítulo II. Conviene recordar
que para su análisis había que considerar uno de los dos estados posibles y
a partir de ello razonar su comportamiento en función de la excitación. En
el Capítulo II empleamos la patilla (-) del AO como entrada de control o de
disparo del “trigger” y vimos con qué tensiones podíamos hacerlo bascular.
Para fijar ideas y valores de tensiones vamos a considerar que el AO está
alimentado con ±12 voltios y que debido a su estructura interna, su tensión
de salida máxima es VOMAX=11V y por la misma razón su tensión de salida
mínima va a ser VOMIN=-11V. Por tanto, los dos estados posibles de este
biestable serán: el que llamaremos estado “1” con vo=VOMAX=+11V y el
que será el estado “0”, con una tensión de salida vo=VOMIN=-11V.
Figura 7](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-201-2048.jpg)























![Diseño con Amplificadores Operacionales 225
Capítulo VI: Sistemas con AO y
Realimentación Global Negativa
VI.1- Introducción
Como anticipamos al final del Capítulo anterior, vamos a ver bajo la
óptica de la realimentación algunas propiedades interesantes de circuitos y
sistemas que hacen uso simultáneo de ambos tipos de realimentaciones y en
los que en todo momento domina la realimentación negativa sobre la
positiva. Ello va a permitir que los AO produzcan una igualdad virtual de
tensiones entre sus entradas (+) y (-), lo que dada la impedancia no nula
existente entre ellas por dentro del AO (esencialmente la Ri de éste) va a
conseguir que hacia el AO no entre ni salga corriente de señal apreciable.
Estaremos pues ante una ITV(SC) que vimos en circuitos con RN, pero
ahora van a aparecer algunos comportamientos inesperados que el MRA no
puede predecir.
Esto no debe extrañarnos porque el MRA fue desarrollado para el
caso de circuitos con sólo Realimentación Negativa y no para el caso de
aquellos con realimentaciones simultáneas en los que dominase la negativa,
que son los que denominaremos circuitos y sistemas con Realimentación
Global Negativa (RGN). El que la aproximación ITV(SC) también se
aplique a estos casos de RGN puede hacer pensar, erróneamente, que se
van a comportar exactamente como circuitos y sistemas con RN, por lo que
el objetivo del presente Capítulo es dejar claro este aspecto y presentar a la
vez algunas aplicaciones interesantes de circuitos y sistemas con RGN.
VI.2- Fuente de corriente Howland
Vamos a presentar en este Apartado un circuito con AO que permite
entregar una cierta corriente IL a una carga RL o extraerla de ella, al ser IL
proporcional a una tensión de control vi que puede ser positiva o negativa.
Estamos hablando por tanto de una fuente de corriente bidireccional
controlada por una tensión de entrada y en concreto nos referimos a una de
las fuentes Howland que aparecen en [7] y que como puede verse en la
Figura 1, es un circuito con doble realimentación, por lo que entraría en la
categoría de sistema electrónico con arreglo a lo que dijimos al respecto en
la Introducción del Capítulo IV. En la Figura 1 se indica que si se cumple
la relación R1R4=R2R3 , la corriente que circula por RL es proporcional a vi
mediante el inverso de R2 cambiado de signo. Si se desean corrientes IL en
el rango del mA con señales de control vi en el rango del voltio, R2 será del
orden del KΩ. En cuanto al signo, diremos que IL fluye hacia masa si la
tensión de entrada vi es negativa y en sentido contrario si vi es positiva.](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-225-2048.jpg)
![226
Figura 1
Esta forma de presentar la fuente Howland suele ser la que aparece
en los textos de Electrónica Analógica y en concreto la que encontró en su
día el autor. Nos referimos al circuito de la Figura 1 junto con las dos
relaciones que allí aparecen, poniendo como premisa la relación entre las
cuatro resistencias para obtener la corriente de salida en función de la
tensión de control. Por su interés posterior, ambas expresiones se recogen
en las ecuaciones (1) y (2), donde se definen algunos factores adicionales
cuyo significado se verá posteriormente.
R3 R4 R R
R1R4 = R2 R3 ⇒ M = = ,K = 2 = 4 (1)
R1 R2 R1 R3
−1
I L = × vi
R (2)
2
Siguiendo la referencia [7], se han definido los factores K y M en la
ecuación (1) e igual que allí, al factor K lo llamaremos “Factor de escala”.
Como para el factor M no se da en [7] ningún nombre, vamos a llamarlo
por ahora “Factor de reparto de tensión” y después ya justificaremos ambos
nombres, con una visión más amplia del sistema completo.
Con los factores K y M sin explicar todavía, la presentación de la
fuente Howland no resulta muy atractiva o al menos esa fue la sensación](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-226-2048.jpg)


![Diseño con Amplificadores Operacionales 229
La entrada de la Figura 2 recuerda la del amplificador inversor con
AO, circuito con RN que creaba una “masa virtual” en la entrada (-) del
AO. Si en la Figura 2 sucediese algo parecido, podríamos aceptar sin
mucha dificultad la frase de [7] en la que se dice:
“…a continuación el factor de escala, K, puede emplearse para establecer
R1, la cual determina, esencialmente, la impedancia de entrada.”
Sin embargo merece la pena obtener la expresión de Zi haciendo uso
de la ITV(SC) que ya empleamos antes en este circuito para obtener IL en
función de vi. Empleando la ecuación (6) se obtiene directamente la tensión
v(+) en función de vi, que resulta ser:
R
v(+) = − L × vi
R (7)
2
La corriente i que entra por R1 como consecuencia de vi es:
vi − v(−)
i= (8)
R1
Aplicando ITV tendremos v(-)=v(+), lo que nos permite sustituir la
ecuación (7) en la (8) y despejar el cociente v/i=Zi. Así obtenemos la
ecuación (9) que ya anticipa un interesante resultado.
vi R RL
Zi = = 1
= R1 × 1 −
R +R
i 1+ RL 2 L (9)
R2
Ese resultado es que la impedancia de entrada no es igual a R1 más
“algo”, sino que es: R1 menos “algo” y ese “algo” depende de RL en una
forma peculiar: si RL→∞ (si quitamos la carga RL) la impedancia de
entrada se anula. Este es un primer aviso de que un circuito con RGN no se
comporta como uno con RN. Retomando la ecuación (9) y empleando la
igualdad R1R4=R2R3 obtenemos la siguiente expresión:
vi R ×R R
Zi = = R1 − 1 L = R1 − R3 × P
i R2 + RL R4 (10)](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-229-2048.jpg)
![230
Ahora, a la vista de la ecuación (10) y de la Figura 2 podemos decir
que la impedancia ZRGN es negativa y además proporcional a R3 mediante
un factor que es la relación de resistencias que fijan la realimentación
positiva del AO. Esta observación nos lleva a la Figura 3 que vamos a
estudiar detenidamente en el próximo apartado.
VI.3- Circuitos de Impedancia Negativa
Aunque éste es un tema muy amplio que el lector interesado puede
consultar en otros textos [5], [22], vamos a presentar bajo el enfoque de
circuitos realimentados las ideas básicas y los circuitos más elementales
con AO que permiten obtener impedancias denominadas “negativas”. En el
caso de resistencias negativas la corriente que circulará a través de una de
ellas para una tensión dada (continua o alterna), lo hará en sentido opuesto
al que tendría en una resistencia de las vistas hasta ahora. En el caso de
bobinas y condensadores “negativos”, las corrientes que los atraviesan en
régimen permanente senoidal presentarán una inversión de fase de 180º (un
cambio de signo) en relación con las corrientes que circularían por sus
correspondientes bobinas y condensadores “positivos” o habituales. Para la
breve presentación mencionada vamos a empezar considerando la Figura 3
y en concreto la impedancia que presenta entre la entrada (-) del AO y
masa, que como acabamos de ver es:
R
Z RGN = − p × R3
R (11)
4
Figura 3](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-230-2048.jpg)

![232
R3 R4
+ 1〈 + 1
(13)
R1 RP
Eliminando los unos y volviendo a invertir los términos (y el signo)
de la desigualdad obtenemos:
RP R1
〈 (14)
R4 R3
Por lo tanto, la condición que garantiza que en el circuito existe
Realimentación Global Negativa puede escribirse como:
R3 RP 〈 R1R4 ⇔ RGN (15)
La condición (15) recuerda en cierto modo la igualdad R1R4=R2R3 de
la fuente Howland de la Figura 1 y considerando que la resistencia RP era la
combinación en paralelo de R2 y RL en dicha fuente, vemos enseguida que
la Fuente Howland posee RGN, porque cualquier RL en paralelo con R2 da
algo menor que R2. Si la fuente se diseñó de forma que cumplía la igualdad
R1R4=R2R3, la desigualdad (15) se cumplirá automáticamente al conectar la
carga RL. Por tanto y aunque todavía no se ve muy bien cómo funciona la
fuente Howland, al menos hemos justificado la validez de nuestro análisis
que partía de la hipótesis fundamental de que en el circuito existía RGN. Y
no sólo eso, sino que también vemos que si con dicha fuente pretendemos
atacar resistencias de carga RL altas, o si desconectamos RL para ver “qué
pasa”, podemos encontrarnos con un circuito inestable, dominado por RGP,
debido a la tolerancia en los valores de las resistencias. De ahí la necesidad
de emplear resistencias de precisión y con baja deriva térmica para el
montaje de fuentes Howland, como puede verse en [7].
Volviendo al circuito de la Figura 3, la existencia de RGN en el
mismo nos permite aplicar ITV(SC), con lo que su funcionamiento se ve
enseguida. Si vi es cero, las tensiones vo, v(+) y v(-) serán cero también,
pero si no es así, la excitación vi hará que aparezca alguna tensión v entre el
punto A y masa. Debido a la ITV(SC) la misma tensión v será creada por el
AO entre su entrada (+) y masa. Esto exige que exista una corriente i2 a
través de R4-RP, lo que a su vez exige una tensión vo=(1+R4/RP)×v en la
salida del AO. Por tanto, la caída de tensión sobre R4 y sobre R3 será la
misma y de valor:](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-232-2048.jpg)

![234
Figura 5
En otras palabras: el circuito de la Figura 5 se puede emplear como
resistencia negativa siempre que la resistencia del circuito al que se aplique
sea mayor que el valor absoluto de la resistencia negativa que se crea entre
su entrada y masa. Así por ejemplo, el circuito de la Figura 5 tal y como
está, sin un generador que le ataque (todo lo cual equivale a tener R1→∞)
será estable, porque en esta situación la realimentación negativa tiende a
ser unitaria: R1/(R1+R3)→1, la mayor posible con un divisor resistivo y va a
dominar a la positiva. Debido a ello se dice que el circuito de la Figura 5 es
“estable frente a circuito abierto”, aunque resulta más claro decir que un
circuito abierto a la entrada del circuito de la Figura 5 garantiza su RGN.
Con unos valores de R3=1KΩ, RA=10KΩ y RB=5KΩ, el circuito de la
Figura 5 presentará una RRGN= -2KΩ a cualquier circuito que se le conecte
con resistencia mayor de 2KΩ y será inestable al conectarlo a circuitos con
resistencias menores de 2KΩ. Ser inestable significa que se convertirá en
un biestable como los vistos en el Capítulo anterior, dejando de ofrecer esa
resistencia negativa dada por la ecuación (18).
Bajo un principio similar funcionarían los circuitos generadores de
capacidades negativas que podemos encontrar en [22]. El circuito utilizado
para ello es el que se muestra en la Figura 6 y la capacidad negativa
aparece entre la entrada (+) del AO y masa. Como puede verse, también
hay doble realimentación en este caso hacia las entradas del AO y por tanto
habrá que asegurar la existencia de RGN en el sistema para que funcione
con arreglo a lo esperado. Esto puede lograrse conectando a la entrada del
circuito una impedancia capacitiva adecuada C’ de modo que el divisor
capacitivo C-C’ realimente a la entrada (+) una señal menor que la que el
divisor resistivo R-R realimenta a la entrada (-). Supondremos que éste es](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-234-2048.jpg)

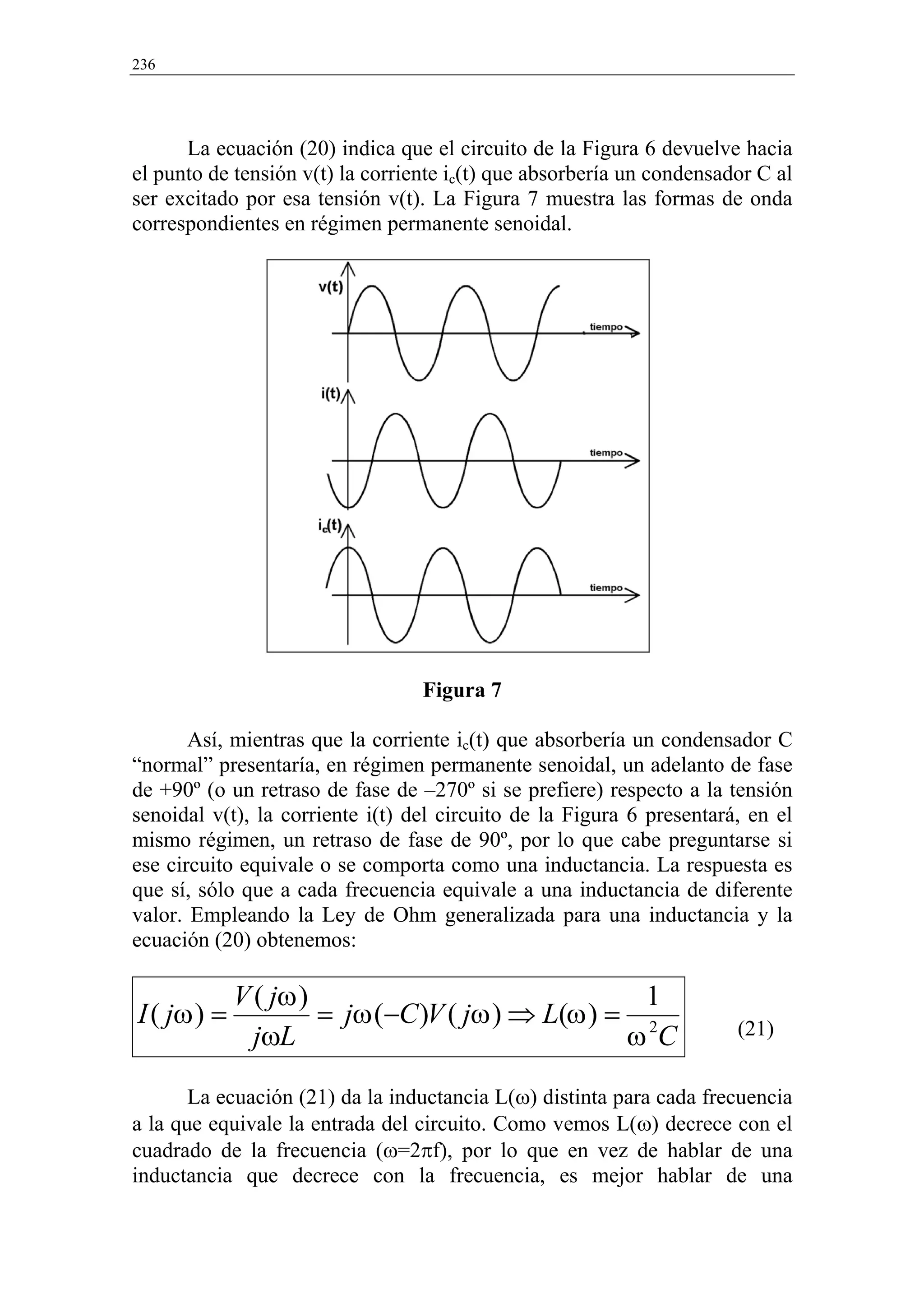
![Diseño con Amplificadores Operacionales 237
capacidad constante con la frecuencia, pero negativa. Esto además sugiere
una posible aplicación del circuito, que es la de compensar capacidades
parásitas que deseemos eliminar o reducir, pero antes de comentar algo más
sobre este tema, veamos qué se necesita para garantizar la existencia de
RGN en el circuito de la Figura 6. Empleando el circuito de la Figura 4 o su
adaptación para impedancias en lugar de resistencias, podemos decir que el
circuito de la Figura 6 tendrá RGN y será por tanto estable, siempre que a
su entrada conectemos una impedancia capacitiva menor que la que ofrece
el condensador C. Este sería el caso para una capacidad Cin mayor que C,
porque se formaría un divisor de tensiones C-Cin que realimentaría menos
del 50% de vo a la entrada (+), mientras que las dos resistencias de valor R
realimentan el 50% de vo a la entrada (-). De esta forma la realimentación
negativa siempre dominaría, incluso en el caso de que la capacidad Cin
llevase conectada en paralelo alguna resistencia Rg, porque la combinación
en paralelo de Cin con esa posible resistencia daría una impedancia
resultante cuyo módulo sería menor que el de la impedancia capacitiva de
Cin. Por tanto, una baja impedancia conectada a la entrada del circuito de la
Figura 6 tiende a hacer el circuito estable porque debilita la realimentación
positiva. De ahí que en la referencia [22] se diga que los circuitos que allí
se presentan (basados en el de la Figura 6), para obtener capacidades
negativas, son “estables en cortocircuito”.
Tras lo que acabamos de comentar sobre una capacidad Cin con algo
en paralelo de tipo resistivo, una aplicación de la capacidad negativa que
hemos visto sería la cancelación de parte de la capacidad debida al cable
apantallado que conectase un sensor de alta impedancia a un amplificador
cuya entrada no permitiese el empleo de técnicas tipo “bootstrap” como las
que vimos en el Capítulo IV (Figura 18). La resistencia de salida del sensor
suele formar con esa capacidad un filtro paso-bajo cuya frecuencia de corte
es inversamente proporcional a dicha capacidad, por lo que su reducción
desde Cin=200pF hasta el valor de 20pF para un sensor con Rg=1MΩ,
permitiría tener un ancho de banda de 8KHz en lugar de los 800Hz debidos
al filtro R-C paso-bajo formado por Rg y Cin. El circuito de la Figura 6 con
R=5KΩ y C=180pF, conectado en paralelo a la entrada del amplificador o a
la salida del sensor con el cable conectado (cuya capacidad de 200 pF
garantizará la existencia de RGN), lograría este efecto.
Por simple cuestión de dualidad tras la obtención de capacidades
negativas mediante el circuito de la Figura 6, surge la pregunta siguiente:
¿Será posible obtener inductancias negativas mediante el mismo circuito,
cambiando el condensador C por una bobina L?. La respuesta es que en
principio parece que sí, pero el circuito así formado va a ser bastante difícil
de manejar y seguramente inestable, porque para señales de muy baja
frecuencia y con más razón en continua (dc), la impedancia de la bobina
tiende a ser cero. Ello haría que la realimentación positiva dominase en el](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-237-2048.jpg)
![238
circuito, dejando de existir la ITV(SC) y perdiendo su utilidad al no tener
RGN sino RGP. Para la finalidad propuesta, el circuito de la Figura 5
también nos daría esa inductancia negativa cambiando R3 por la bobina L,
siendo estable de cara a bajas frecuencias y a dc. Sin embargo habría que
tener cuidado con las altas frecuencias para las que la impedancia de la
bobina aumentaría, debilitando por tanto la realimentación negativa. Esto
haría que el circuito pasase a tener RGP, volviéndose inestable y perdiendo
su utilidad. Como en general se prefiere evitar el empleo de bobinas por su
volumen y características circuitales, peores que las de los condensadores,
dejaremos el tema de inductancias negativas y nos quedaremos con las
simples ideas presentadas sobre circuitos estables frente a cortocircuito y
frente a circuito abierto que permiten obtener resistencias y capacidades
negativas. Para el lector interesado en este tema de impedancias negativas
obtenidas mediante AO y condensadores, la referencia [22] ofrece ejemplos
de circuitos que usan resistencias negativas dependientes de la frecuencia y
que aparecen como FDNR (Frequency Dependent Negative Resistances).
VI.4- Sistemas con ambas realimentaciones equilibradas
Cuando analizamos la fuente de corriente Howland y obtuvimos las
ecuaciones que regían su comportamiento, no vimos su funcionamiento de
una forma clara o intutiva. Sin embargo hicimos algún avance importante,
especialmente al emplear el circuito de la Figura 4 para ver si existía RGN
en estos circuitos con AO y realimentaciones dobles. Vamos a considerar
ahora la fuente Howland de la Figura 1, sólo que sin la resistencia RL, tal y
como aparece en la Figura 8. Recordamos que las cuatro resistencias que
rodean al AO cumplen la relación: R1R4=R2R3 y ello significa que, para
cualquier tensión vo que haya en la salida, las fracciones de esa señal que
los divisores resistivos R1-R3 y R2-R4 realimentan a las entradas (-) y (+)
del AO son iguales. Considerando infinita la ganancia Ad del AO podemos
tener esas dos tensiones iguales en las entradas (+) y (-) con una tensión de
salida vo cualquiera no nula. La ganancia finita, por ejemplo Ad=106, de un
AO real, requerirá que si a la salida hay una tensión vo de 3 voltios, la señal
de la patilla (+) sea 3 microvoltios mayor que la de la patilla (-) del AO. Sin
embargo, esa pequeña diferencia de 3µV entre las dos tensiones puede
considerarse nula a efectos prácticos, por lo menos en lo que respecta a los
valores de las cuatro resistencias ligados por la relación R1R4=R2R3. Piense
el lector en un caso práctico en el que cada uno de los divisores resistivos
R1-R3 y R2-R4, atenúe por 3 la señal vo. La tensión vo de 3 voltios dará lugar
a una tensión realimentada de 1 voltio en cada entrada del AO. El que esa
tensión sea 1 voltio exactamente o difiera de este valor en 3 µV es algo que
queda más allá de la precisión que podemos tener en los valores de las
resistencias aunque las tomemos con el 0.1 por mil de precisión. Por tanto](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-238-2048.jpg)

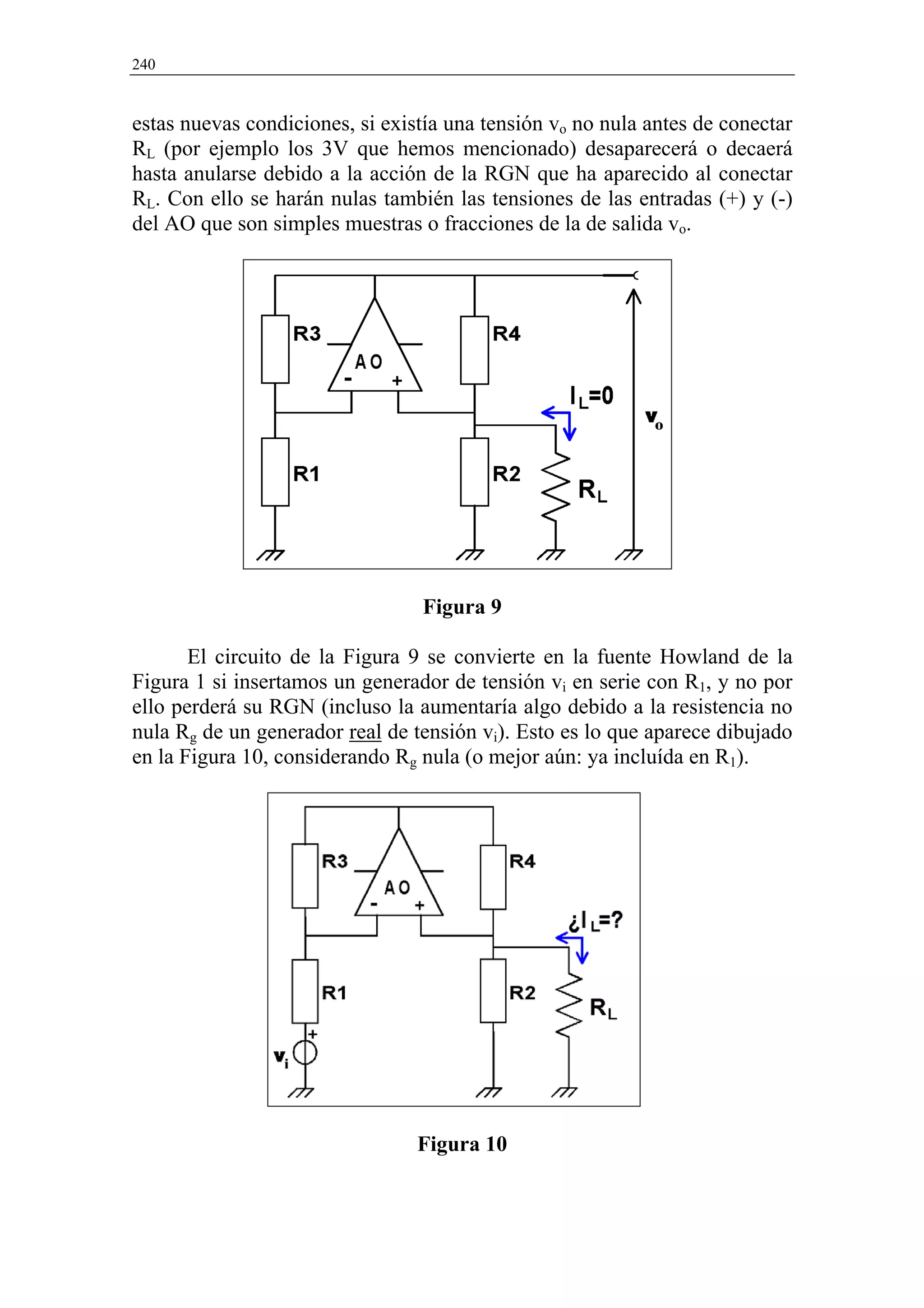
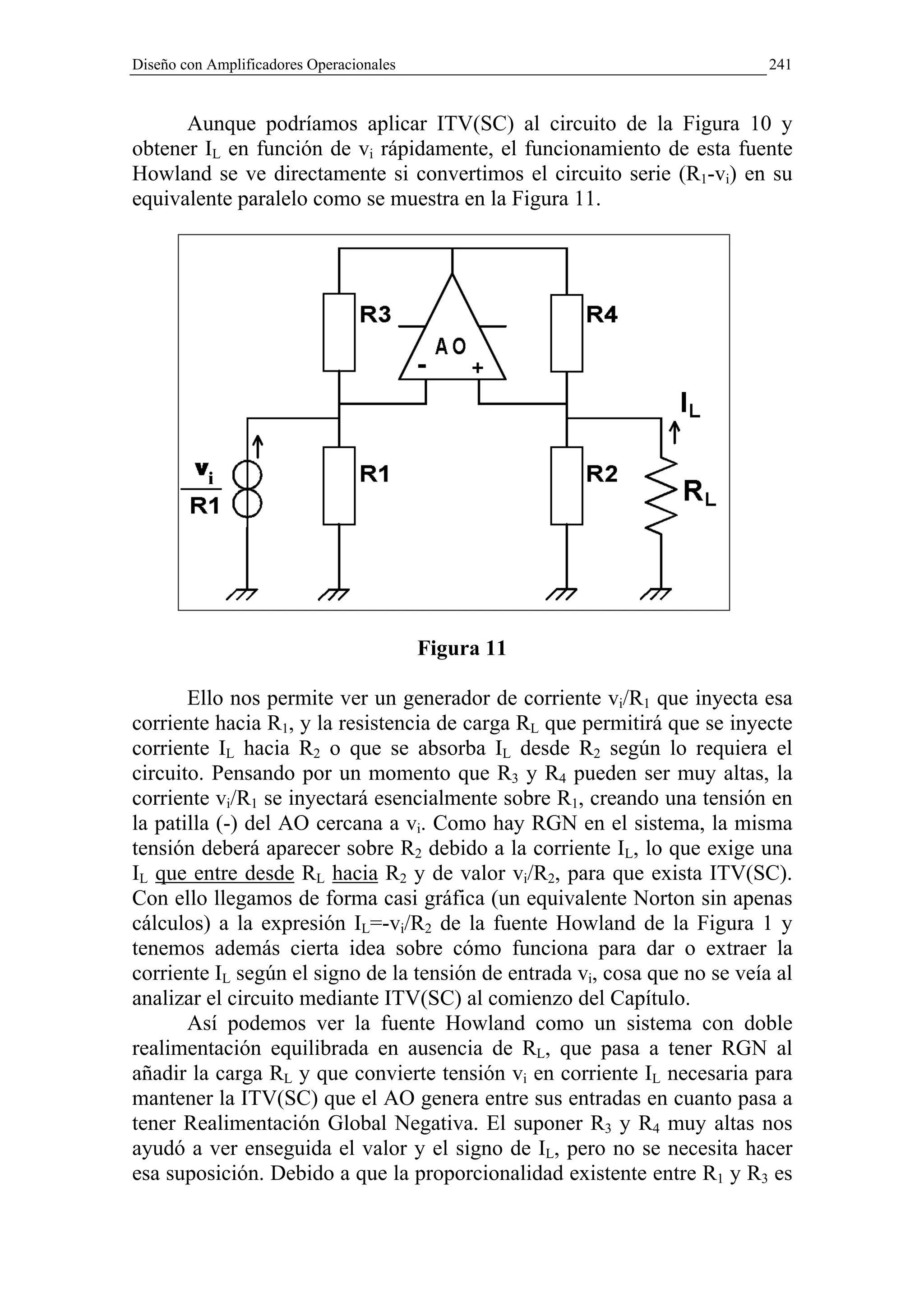
![242
la misma que entre R2 y R4, basta considerar que la corriente vi/R1 de la
Figura 11 se inyecta sobre R1R3 que es la misma fracción de R1 que
R2R4 lo es de R2. Esta es la situación que obtenemos al anular vo en la
Figura 11 para superponer los efectos de vi y de IL por separado, de donde
se obtiene la relación IL=-vi/R2 al aplicar ITV(SC).
A la vista del circuito de la Figura 11 resulta fácil entender la otra
versión de la fuente Howland presentada en [7] en la que el generador vi se
conecta entre R2 y masa en lugar de estar entre R1 y masa como en la
Figura 10. Al convertir a su equivalente paralelo el generador vi (ahora en
serie con R2) aparece directamente que la corriente IL saliente hacia la carga
RL debe ser IL=vi/R2 para que exista la ITV(SC) que genera la RGN. Es lo
que se muestra en la Figura 12 y de esta forma la corriente a través de RL
con el sentido dibujado en la Figura 1 resulta ser: IL=+vi/R2 si el generador
de control vi de la Figura 1 se sitúa entre R2 masa, conectando a masa la
patilla de R1 a la que antes iba conectado. Esta versión “no-inversora” de la
fuente Howland presenta ciertas diferencias en cuanto a su impedancia de
entrada respecto a la versión “inversora” que hemos visto. La diferencia es
que dicha impedancia de entrada (resistencia en este caso) puede ser
negativa, cosa que sucede cuando la resistencia de carga RL es mayor que
R2 [23]. La Figura 12 permite ver este efecto de forma rápida porque ante
una tensión de control vi aplicada debajo de R2, la tensión encima de R2, es
decir: la de la entrada (+) del AO será: vi×RL/R2.
Figura 12](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-242-2048.jpg)












![Diseño con Amplificadores Operacionales 255
Bibliografía
[1] Optoelectronique
E. Rosencher, B. Vinter
Masson S.A. París. (1998). ISBN: 2-225-82935-7.
[2] Signals and systems
A.V. Oppenheim, A.S. Willsky, I.T. Young.
Prentice-Hall signal processing series. (1983). ISBN: 0-13-811175-8.
[3] Fourier Analysis with applications to boundary value problems
M.R. Spiegel.
Schaum´s outline series, McGraw-Hill. (1974). ISBN: 0-07-060219-0.
[4] Complex variables and the Laplace transform for engineers
W.R. LePage.
Dover Publications Inc. New York. (1980). ISBN: 0-486-63926-6.
[5] Análisis de circuitos
W. Warzanskyj.
Dpto. Publicaciones E.T.S.I.T. Madrid. (1977). ISBN: 84-7402-045-X.
[6] Analog integrated circuits (Second Edition)
P.R. Gray, R.G. Meyer
John Wiley & Sons, New York. (1984). ISBN: 0-471-81454-7.
[7] Amplificadores Operacionales Integrados
W.G. Jung
Editorial Paraninfo S.A. Madrid. (1991). ISBN: 84-283-1833-6.
[8] Amplificadores Operacionales y Circuitos Integrados Lineales
J.M. Fiore
Int. Thomson Editores Spain. (2002). ISBN: 84-9732-099-9.
[9] General Purpose Linear Devices, Databook
National Semiconductor Corp. (1989). Santa Clara, California (USA)
[10] Low-Noise Electronic Design
C.D. Motchenbacher, F.C. Fitchen
John Wiley & Sons, New York. (1973). ISBN: 0-471-61950-7.
[11] Thermal agitation of electricity in conductors
J.B. Johnson
Physical Review, 32, pp 97, 1928
[12] Thermal agitation of electric charge in conductors
H. Nyquist
Physical Review, 32, pp 110, 1928](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-255-2048.jpg)
![256
[13] Design of Analog CMOS Integrated Circuits (Preview Edition)
B. Razavi
McGraw-Hill. (2000). ISBN: 0-07-237371-0.
[14] Design with Operational Amplifiers and Analog Integrated Circuits (Second Ed.)
S. Franco
McGraw-Hill. (1998). ISBN: 0-07-115280-6.
[15] Linear Databook
Linear Technology Corporation. (1990). Milpitas, California (USA)
[16] Noise Reduction Techniques in Electronic Systems (Second Edition)
H.W. Ott
John Wiley & Sons, New York. (1988). ISBN: 0-471-85068-3.
[17] EMC at component and PCB level
M. O´Hara
Newnes (Butterworth-Heinemann). (1998). ISBN: 0-07-115280-6.
[18] Linear Applications Handbook: A guide to linear Circuit Design
Linear Technology Corporation. (1990). Milpitas, California (USA)
[19] A practical introduction to Electronic Circuits (Third Edition)
M. H. Jones
Cambridge University Press. (1995). ISBN: 0-521-47879-0
[20] Photodiode Amplifiers, Op Amp Solutions
J. Graeme
McGraw-Hill. (1996). ISBN: 0-07-024247-X.
[21] Analog Integrated Circuits Databook (Volume 10)
Precision Monolithics Inc. (1990). Santa Clara , California (USA).
[22] Analog Circuits Cookbook (Second Edition)
I. Hickman
Newnes (Butterworth-Heinemann). (1999). ISBN: 0-7506-4234-3.
[23] Convertidor DC-AC de mediana potencia para automóvil
F. J. Martínez
Proyecto Fin de Carrera. ETSI Telecomunicación-UPM. (2004)
***](https://image.slidesharecdn.com/textom2-110613054151-phpapp01/75/Texto-m2-256-2048.jpg)