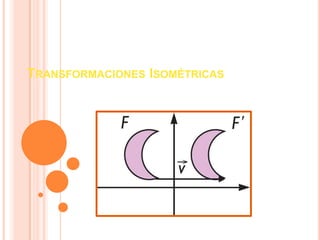
Este documento describe las transformaciones isométricas de figuras geométricas planas, incluyendo traslaciones, rotaciones y simetrías. Define una transformación isométrica como un cambio de posición que no altera la forma ni el tamaño de la figura. Explica que las traslaciones involucran un cambio de lugar determinado por un vector, las rotaciones implican un giro alrededor de un punto fijo, y las simetrías producen un reflejo de la figura respecto a un eje o punto. Además, señala

1. TRANSFORMACIONES ISOMÉTRICAS

2. Objetivo fundamental
 Caracterizar y efectuar
transformaciones isométricas
de figuras geométricas
planas, reconocer algunas de
sus propiedades e identificar
situaciones en contextos
diversos que corresponden a
aplicaciones de dichas
transformaciones.

3. ISOMETRÍA Y TRANSFORMACIONES
ISOMÉTRICAS
 Se denomina transformación
isométrica de una figura en el
plano aquella transformación
que no altera ni la forma ni el
tamaño de la figura en cuestión
y que solo involucra un cambio
de posición de ella resultando
que la figura inicial y la final
son semejantes, y
geométricamente congruentes.

4.  Respecto a la isometría y a las posibilidades de
transformaciones de figuras, se pueden describir
tres tipos de ejecución: por traslación, por
rotación y simetría (o reflexión).
 Cualquiera que sea el método aplicado para
realizar una transformación isométrica en un
plano es imprescindible trabajar sobre un sistema
de coordenadas.

5. SISTEMA DE COORDENADAS
 Un sistema de coordenadas
bidimensional (en un plano) es
un sistema en el cual un punto
puede moverse en todas
direcciones, manteniéndose
siempre en el mismo plano.
 Este sistema está formado por
dos rectas perpendiculares
entre sí llamadas ejes de
coordenadas (eje de las x y eje
de las y).

6.  El origen del sistema divide a cada eje
en dos semi-ejes:
 (a) las ABSCISAS ubicadas a la
derecha del eje Y, respecto del origen,
son positivas y las ubicadas a la
izquierda son negativas.
 (b) las ORDENADAS ubicadas hacia
arriba del eje X, respecto del origen,
son positivas y las ubica-das hacia
abajo son negativas.
 Los ejes dividen al plano en cuatro
partes llamadas cuadrantes,
numerados según se muestra en la
Figura 1.

7. Transformaciones isométricas por
Traslación
 En una transformación
isométrica por traslación se
realiza un cambio de posición
de la figura en el plano. Es un
cambio de
lugar, determinado por un
vector.

8.  Las traslaciones isométricas están
marcadas por tres elementos:
 La dirección, si es horizontal, vertical un oblicua.
 El sentido, derecha, izquierda, arriba y abajo.
 Y la magnitud del desplazamiento que se refiere a
cuánto se desplazó la figura en una unidad de medida.

9. Ejemplo
 El punto A se traslada tres unidades hacia la derecha y 3
unidades hacia abajo, por lo que el vector de traslación
se podría representa por el par ordenado (3,-3)

10. Ejemplo 2
El punto A(2,4) se traslada según el vector (4,0)
 Para obtener el punto A’ , se deben sumar las
coordenadas correspondientes del punto A y el vector,
es decir (2,4) + (4,0) = (2+4, 4+0) = (6+4)

11.  Al igual que las traslaciones, las reflexiones
también se denominan isometrías
 o movimientos rígidos,
 porque se mueven las figuras sin
distorsionarlas, sin apretarlas ni expandirlas.

12. Transformaciones isométricas por
Rotación
 Es una figura que se mueve rotándose con un ángulo hacia
un punto determinado, es decir, es un movimiento de
cambio en la orientación de un cuerpo; de forma que,
dado un punto cualquiera del mismo, este permanece a
una distancia constante de un punto fijo.

13. En una rotación se identifican tres
elementos:
 El punto de rotación (centro de
rotación), punto en torno al cual
se efectúa la rotación.
 La magnitud de rotación , que
corresponde al ángulo, éste está
determinado por un punto
cualquiera de la figura, el centro
de rotación (vértice del ángulo) y
el punto correspondiente de la
figura obtenida después de la
rotación
 El sentido del giro, positivo
(antihorario), negativo (horario)

14. Ejemplo
 Efectuar una rotación de 90º en sentido antihorario
respecto al origen.

16. ¡Las rotaciones siempre
preservan
 distancias y ángulos!

17. Transformaciones isométricas por
Simetría
La figura del escarabajo como de la mariposa se ven simétricas, pues si trazamos
una línea recta en el centro de cada una, la parte que está a la derecha de la línea
sería exactamente igual a la parte que está a la izquierda de esa misma línea.
Sobre la base de estos dos ejemplos, se descubre fácilmente que hay una
transformación que hace que la parte izquierda de la figura sea un reflejo de la
parte derecha sin cambiar su forma ni sus dimensiones.
Esto nos lleva a afirmar que Simetría es la correspondencia exacta (un reflejo) en
la disposición regular de las partes o puntos de un cuerpo o figura con relación a
un punto (centro), una recta (eje de simetría) o un plano.

18.  Se puede considerar
una simetría como
aquel movimiento
que aplicado a una
figura geométrica,
produce el efecto de
un espejo.

19. Simetría central
 La simetría central, en geometría, es una transformación en la que a cada
punto se le asocia otro punto, que debe cumplir las siguientes condiciones:
 a) El punto y su imagen estén a igual distancia de un punto llamado centro de
simetría.
 b) El punto, su imagen y el centro de simetría pertenezcan a una misma
recta.

20. Ejemplo
 Reflejar el cuadrado ABCD en torno al origen

22. Simetría axial
 La simetría axial, en geometría, es una transformación respecto de un
eje de simetría, en la cual, a cada punto de una figura se asocia otro
punto llamado imagen, que cumple con las siguientes condiciones:
 a) La distancia de un punto y su imagen al eje de simetría, es la misma.
 b) El segmento que une un punto con su imagen, es perpendicular al eje
de simetría.

23. Ejemplo
 Reflejar el cuadrado ABCD respecto al eje Y

24. Ejemplo 2
 Reflejar el cuadrado ABCD en torno al eje X

25. Transformaciones isométricas en la
vida cotidiana:
 Traslación: al moverse ,al caminar.
 Rotación: al girar, al dar vueltas.
 Simetría: un espejo al mirarse.

26. Importante
 Todatransformación isométrica, mantiene la
forma y tamaño de una figura geométrica, por lo
tanto el perímetro y el área no sufren variación.