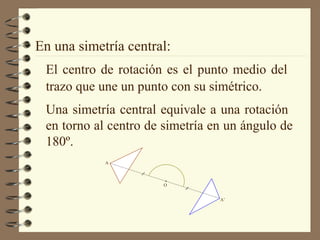
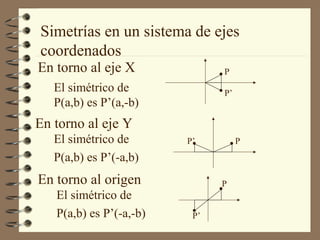
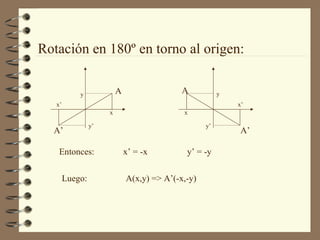
Este documento describe las transformaciones isométricas, que son movimientos que no alteran la forma ni el tamaño de una figura. Explica tres tipos principales: simetrías o reflexiones, traslaciones y rotaciones. Las simetrías incluyen reflexiones axiales y centrales. Las traslaciones implican deslizar una figura manteniendo su forma. Las rotaciones implican girar una figura en torno a un punto central sin cambiar su forma.

1. TRANSFORMACIONES
ISOMÉTRICAS
En una transformación isométrica:
1) No se altera la forma ni el tamaño de la
figura.
2) Sólo cambia la posición (orientación o
sentido de ésta).

2. Tipos de transformaciones isométricas
Simetrías o reflexiones
Traslaciones
Rotaciones o giros
Axial o especular
Central

3. Simetrías o reflexiones
Se puede considerar una simetría como
aquel movimiento que aplicado a una
figura geométrica, produce el efecto de un
espejo.

4. Tipos de simetrías
Axial (reflexión respecto de un eje)
Central (reflexión respecto de un punto)
O

5. En una simetría axial:
Cada punto y su imagen o simétrico
equidistan del eje de simetría.
El trazo que une un punto con su simétrico
es perpendicular al eje de simetría.
A’
A

6. En una simetría central:
El centro de rotación es el punto medio del
trazo que une un punto con su simétrico.
Una simetría central equivale a una rotación
en torno al centro de simetría en un ángulo de
180º.
O
A’
A

7. Simetrías en un sistema de ejes
coordenados
En torno al eje X
El simétrico de
P(a,b) es P’(a,-b)
En torno al eje Y
El simétrico de
P(a,b) es P’(-a,b)
En torno al origen
El simétrico de
P(a,b) es P’(-a,-b)
P
P’
·
·
P’· · P
·P
·P’

8. Traslaciones
Se puede considerar una traslación como el
movimiento que se hace al deslizar una
figura, en línea recta, manteniendo su
forma y tamaño.

9. En una traslación:
Al deslizar la figura todos los puntos
describen líneas rectas paralelas entre
sí.

10. En una traslación se distinguen tres
elementos:
Dirección (horizontal, vertical u oblicua).
Sentido (derecha, izquierda, arriba, abajo).
Magnitud del desplazamiento (distancia
entre la posición inicial y final de
cualquier punto)

11. Traslaciones en un sistema de ejes
coordenados
En este caso se debe señalar las
coordenadas del vector de traslación.
Estas son un par ordenado de números
(x,y), donde x representa el
desplazamiento horizontal e y
representa el desplazamiento vertical.

12. En el par ordenado la primera componente
recibe el nombre de abscisa y la segunda
componente el nombre de ordenada.

13. Traslaciones de puntos en el sistema
cartesiano.
·A(4,6)
·
A’ (2,3)
Traslación de A(4,6)
a través del vector v(-2,-3)
Traslación de B(-5,2)
a través del vector v(4,4)
·
B(-5,2)
· B’(-1,6)
Traslación de C(-4,-2)
a través del vector v(7,1)
·
C(-4,-2)
· C’(3,-1)

14. En la abscisa:
Signo positivo: desplazamiento hacia la derecha.
Signo negativo: desplazamiento hacia la izquierda.
En la ordenada:
Signo positivo: desplazamiento hacia arriba.
Signo negativo: desplazamiento hacia abajo.

15. Rotaciones o giros.
Una rotación es el movimiento que se
efectúa al girar una figura en torno a un
punto.
Este movimiento mantiene la forma y el
tamaño de la figura.

16. En una rotación se identifican tres elementos:
El punto de rotación (centro de rotación), punto en torno al cual se
efectúa la rotación.
La magnitud de rotación, que corresponde al ángulo, éste está
determinado por un punto cualquiera de la figura, el centro de
rotación (vértice del ángulo) y el punto correspondiente de la figura
obtenida después de la rotación.
El sentido de giro, positivo (antihorario), negativo (horario)
O
M
M’
N’
N
.

17. Rotación en 90º en torno al origen:
A
x
y
A
x
y
A’
y’
x’
x’
y’
A’ Entonces: x’ = -y y’ = x
Luego: A(x,y) => A’(-y,x)

18. Rotación en 180º en torno al origen:
A
x
y
x’
A’
y’
A
x
y
x’
A’
y’
Entonces: x’ = -x y’ = -y
Luego: A(x,y) => A’(-x,-y)

19. Importante
Toda transformación isométrica,
mantiene la forma y tamaño de una
figura geométrica, por lo tanto el
perímetro y el área no sufren
variación.