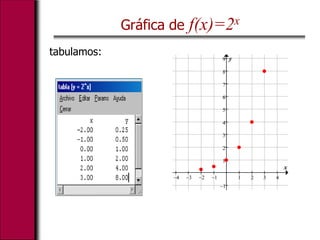
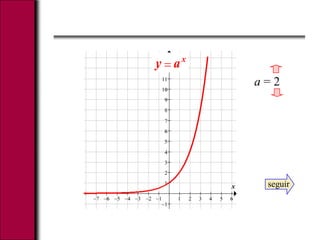
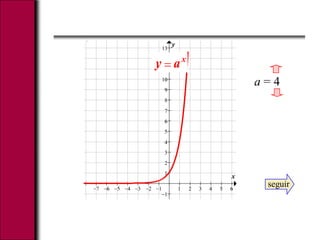
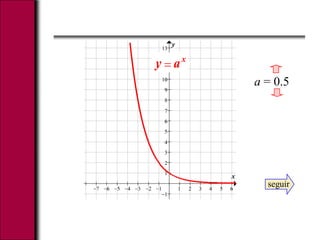
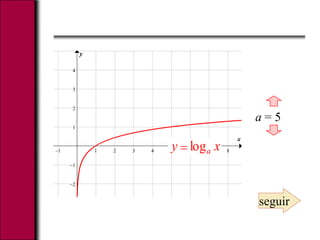
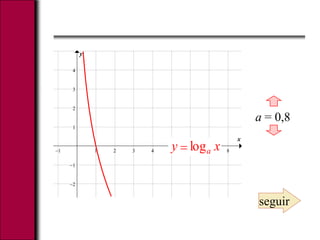
El documento explica las funciones exponenciales y logarítmicas. Define una función exponencial como f(x)=ax, donde a es la base. Las gráficas de funciones exponenciales con a>1 son crecientes y cóncavas hacia arriba, mientras que las de 0<a<1 son decrecientes. También define el logaritmo y explica que las gráficas logarítmicas son simétricas a las exponenciales, siendo cóncavas hacia abajo para bases mayores a 1 e hacia arriba para bases menores. Finalmente

2. Función exponencial
Una función exponencial f está
dada por:
f(x) = ax
donde x es cualquier número real,
a > 0 y a ≠ 1. El número a se
llama base.

3. x
y
tabulamos:
Gráfica de f(x)=2x

4. x
y
x
y 2
La curva se acerca al eje x pero no lo toca ni
lo corta. El eje x es una asíntota horizontal.
La gráfica es:
Creciente
Cóncava hacia arriba.
Pasa por el punto (0; 1); (1; 2).

5. x
y
a = 2
seguir
x
ay

6. x
y
a = 3
seguir
x
ay

7. x
y
a = 4
seguir
x
ay

8. x
y
a = 5
seguir
x
ay

9. x
y
a = 1.5
seguir
x
ay

10. x
y
a = 1.2
seguir
x
ay

11. x
y
a = 1
seguir
x
ay

12. tabulamos…
x
y
Gráfica de f(x)=(½)x

13. x
y
x
y
2
1 La gráfica es:
Decreciente
Cóncava hacia arriba.
Pasa por el punto (0; 1); (1; ½ ).
La curva se acerca al eje x pero no lo toca ni
lo corta. El eje x es una asíntota horizontal.

14. x
y
a = 0.5
seguir
x
ay

15. x
y
a = 0.33
seguir
x
ay

16. x
y
a = 0.25
seguir
x
ay

17. x
y
a = 0.2
seguir
x
ay

18. Muy importante!!
x
y
f(x)=
a > 1
x
a
);1( 1
a
);2( 2
a
);1( 1
a
)1;0(
Función creciente
Rango: (0; ∞)
Dominio:
Asíntota: Eje x
Gráfica cóncava
hacia arriba
Conclusiones

19. OJO!!
x
y
f(x)=
0 < a < 1
x
a
)1;0(
);1( 1
a
);2( 2
a
);1( 1
a
);2( 2
a
Función decreciente
Rango: (0; ∞)
Dominio:
Asíntota: Eje x
Gráfica cóncava
hacia arriba
Conclusiones

20. n
1 S/.2,00000
2 S/.2,25000
3 S/.2,37037
4 S/.2,44141
12 S/.2,61304
52 S/.2,69260
365 S/.2,71457
8760 S/.2,71813
525600 S/.2,71828
…. …..
n
)
n
1(1A
El monto obtenido crece
como puede apreciarse
pero solo hasta cierta
cantidad, es decir
cuando n se hace muy
grande…
....718281828,2
11lim
e
n
e
n
n
El número e

21. Gráfica de f(x) = ex
x
y
x
ey
Función creciente
Rango: (0; ∞)
Dominio:
Asíntota: Eje x
Gráfica cóncava
hacia arriba
x ex
0 1
1 2,71..
2 7,38..

22. x
y
x
y 3
x
y 2
x
ey
Gráfica de f(x) = ex

23. f
g
Note que: y = f(x) y x = g(y)
g(y)
x. .y = f(x)
Diagrama de una función inversa

24. Definición
Sean f y g dos funciones tales que:
dominio de f es D y rango C
dominio de g es C y rango D
g es la inversa de f si se cumple:
– g(f(x)) = x para todo x en D
– f(g(x)) = x para todo x en C

25. Función logarítmo
loga x = y ay = x
a>1 y a≠1
• El logaritmo de un número x en una base
a es el exponente y al que hay que
elevar la base para obtener el número.

26. Ecuación logarítmica Ecuación exponencial
NMalog MaN
2100log10
201,0log10
2
1
49 7log
100102
01,010 2
7492
1
Exponenciales y logarítmos

27. xxy y
2log2
¼ -2
½ -1
1 0
2 1
4 2
8 3
y
x 2 y
x
y
graficamos…
Gráfica de f(x) = log 2 x

28. x
y
xy 2log
Se observa que ahora la
asíntota vertical es el eje y
La gráfica es creciente
y cóncava hacia abajo
y pasa por (1; 0)
¿cómo se compara esta gráfica con la exponencial de
base 2?

29. ¿y cómo varía la gráfica al cambiar la base a?
x
y
x
xf 2)(
xxg 2log)(
xy
(2; 4)
(4; 2)
Las gráficas son simétricas
respecto a la recta y = x.
Cada punto (a; b) de la
curva exponencial tiene su
simétrico de la forma (b; a)
en la curva logarítmica.

30. x
y
a = 2
seguir
xy alog

31. x
y
a = 2,5
seguir
xy alog

32. x
y
a = 3
seguir
xy alog

33. x
y
a = 3,5
seguir
xy alog

34. x
y
a = 4
seguir
xy alog

35. x
y
a = 4,5
seguir
xy alog

36. x
y
a = 5
seguir
xy alog

37. x
y
a = 1,6
seguir
xy alog

38. x
y
a = 1,2
seguir
xy alog

39. a = 0,8
x
y
seguir
xy alog

40. a = 0,7
x
y
seguir
xy alog

41. a = 0,6
x
y
seguir
xy alog

42. a = 0,5
x
y
seguir
xy alog

43. a = 0,4
x
y
seguir
xy alog

44. x
y
xy alog
a > 1
Función creciente
Dominio: (0; ∞)
Rango:
Asíntota: Eje y
Gráfica cóncava
hacia abajo
base
a
Conclusiones

45. x
y
xy alog
0 < a < 1
Función decreciente
Dominio: (0; ∞)
Rango:
Asíntota: Eje y
Gráfica cóncava
hacia arriba
a
base
Conclusiones

46. Propiedades de logarítmos
eedcb
b
a
a
mb
a
n
m
a
a
n
a
xmx
nm
n
m
nmnm
abya
adcba
x
x
b
m
b
m
b
b
n
b
a
m
a
bbb
bbb
y
b
b
n
loglog.log.log.log)8
log
log
log)7
)6
loglog)5
log
1
log)4
loglog)3
logloglog)2
loglog.log)1
log
log

47. Para cualquier número positivo x.
xx loglog10
Logarítmo decimal o común
El logaritmo log10 x se llama
logaritmo común de x y su forma
abreviada es log x.

48. Son aquellos cuya base es el número
e ≈ 2,7182818..
Para cualquier número positivo x.
xxe lnlog
Logaritmo natural

49. x
y
e
Posee las
características de
toda gráfica
logaritmica de
base mayor que 1.
Gráfica de f(x) = ln x

51. Resolver: 15
)5(2 xx
EXPONENCIALES
0)5)(2(
55 xx
0)5)(2( xx
05210 2
xxx
01072
xx
0)2)(5( xx
0205 xx
25 xx
C.S: {2;5}

52. Resolver:
EXPONENCIALES
C.S:
25 272 12 x xx x
aa
25
27
2
12
x
x
x
x
aa
25
27
2
12
x
x
x
x
)2)(27()25)(12( xxxx
41272910 22
xxxx
042129710 22
xxxx
06213 2
xx
25 272 12 x xx x
aa
)(2
))((42
a
cabb
x
)2(2
)2)(1(477 2
x
4
8497
x
4
417
x
0272
xx
4
417
;
4
417

53. Resolver:
LOGARITMOS
2
log216loglog3
x
x
2
3
2
log16loglog
x
x
23
2
log
16
log
xx
23
216
xx
416
23
xx
4
16
2
3
x
x
4x
C.S: {4}

54. Resolver:
LOGARITMOS
Rpta: 4
49log25log3log4log 2759
2
2
2
75
2
3
7log.5log.3log.2log 2
7log.5log.3log.2log
2
2.2.2
2753
3log.5log.7log.2log.4 5723
3log.4 3
)1.(4
4

55. Resolver:
LOGARITMOS
Rpta: 32
2log3
243
2log5 3
)3(
2log5 3
3
5
3 2log
3
5
2
32

56. Resolver:
LOGARITMOS
Rpta:
122 23x
12log2log 23x
12log2log)23( 22x
3log2log2log2log)23( 2222x
3log1123 2x
2log
3log
43x
30.0
48.0
43x
46,13x
6,53x
.)(87,1 aproxx

57. Para cualesquier números positivos a, M y N, a ≠ 1 y
cualquier número real k:
MkM
NM
N
M
NMNM
ka
a
a
k
a
aaa
aaa
k
a
a
a
loglog.6
logloglog.5
logloglog.4
log.3
01log.2
1log.1
Propiedades de logarítmos