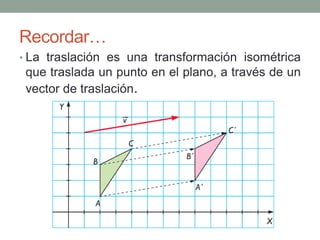
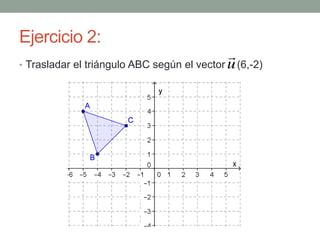
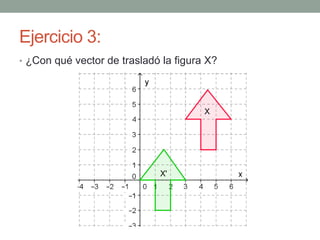
Las transformaciones isométricas incluyen traslaciones, que desplazan un punto en el plano mediante un vector determinado. Se presentan ejemplos de cómo calcular las nuevas coordenadas de un punto traslacionado y ejercicios para practicar la ubicación y traslado de puntos y figuras en el plano. Se concluye que, para determinar un punto trasladado o el vector de traslación entre dos puntos, se utilizan operaciones de suma y resta de sus coordenadas.

1. TRANSFORMACIONES ISOMÉTRICAS:
TRASLACIONES
Prof: Jennifer Corvalán R.

2. Recordar…
• La traslación es una transformación isométrica
que traslada un punto en el plano, a través de un
vector de traslación.

3. Ejemplo:
• Trasladar el punto A( 2,3) según el vector (4,-1)

4. • Al mover el punto A se obtiene su imagen que es
el punto A’.
• Para determinar las coordenadas de la imagen,
se puede graficar o desarrollar la operatoria de
vectores.
• Es decir: A(2 , 3)
+ (4,-1)
A’(6 , 2)

5. Ejercicio 1:
• Ubicar los siguientes puntos en el plano y trasladarlos
según el vector dado:
• 1) A(3,2) vector:
• 2) B(-2,5) vector:
• 3) C(0,3) vector:
• 4) D(-4,-1) vector:
• 5) E(3,-2) vector:

6. Ejercicio 2:
• Trasladar el triángulo ABC según el vector (6,-2)

7. Ejercicio 3:
• ¿Con qué vector de trasladó la figura X?

8. Conclusiones
• Dado un punto A y un vector de traslación , se puede
determinar el punto trasladado A’, con la operación A+
• Dado un punto A y el punto trasladado A’, se puede
determinar el vector de traslación restando el punto final
menos el punto inicial, es decir: A’ – A

9. Ejercicio final
• Utilizando operatoria de vectores, determinar lo siguiente:
• 1) A’ , considerando A(4, 5) y (-3,2)
• 2) Vector , si A(2,-1) y A’(7,4)