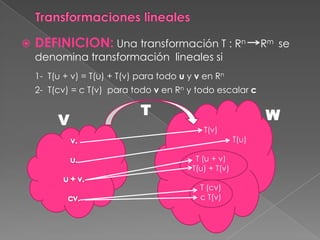
Este documento resume las transformaciones lineales. Define transformaciones lineales como funciones entre espacios vectoriales que preservan la suma y la multiplicación por escalares. Presenta ejemplos de transformaciones lineales como reflexiones y rotaciones. Explica que las transformaciones lineales pueden representarse mediante matrices y que la composición y inversa de transformaciones lineales también son transformaciones lineales.

1. Espacio curricular: Algebra III
Profesor: Petrovic Héctor

2.  Son funciones entre espacios vectoriales que
preservan las cualidades de los espacios
vectoriales. Es decir, de funciones que preservan la
suma y la multiplicación por escalares.
 TA: R2 R3
1 0 x
A = 2 -1 y V=
y
3 4
x x
TA y = 2x – y
3x + 4y

3.  DEFINICION: Una transformación T : Rn Rm se
denomina transformación lineales si
1- T(u + v) = T(u) + T(v) para todo u y v en Rn
2- T(cv) = c T(v) para todo v en Rn y todo escalar c
T W
V
T(v)
T(u)
T (u + v)
T(u) + T(v)
T (cv)
c T(v)

4. Transformación lineal
 TEOREMA 1
Sea A una matriz de m x n . Entonces la
transformación matricial TA: R n R m definida por.
TA(x) = A x (para x en Rn)
es una transformación lineal.
EJEMPLO: Sea F: R2 R2 la transformación que manda a
cada punto hacia su punto de reflexión sobre el eje x.
y
(1;2)
(X ;Y)
x
(x;-y)
(1;-2)

5. Transformaciones lineales
EJEMPLO: Sea R: R2 R2 la transformación que gira
cada punto a 90o en el sentido contrario de las
manecillas del reloj con respecto al origen.

6. Transformaciones lineales
Este tipo de ejemplo lo podemos ver en la
vida diaria como en la naturaleza

7. Transformaciones lineales
 TEOREMA 2
Sea T: Rn Rm una transformación
lineal. Entonces T es una transformación matricial.
Mas específicamente, T = TA, donde A es la matriz de
mxn
 A = T(e1); T(e2); ... ; T(en)
Esta matriz se la conoce como matriz estándar de
la transformación lineal T

8. Nuevas transformaciones lineales a
partir de las antiguas
TEOREMA 3
Sean T: Rm Rn y S: Rn Rp
transformaciones lineales. Entonces S T: Rm Rp es
una transformación lineal. Además, sus matrices
estándar se encuentran relacionadas mediante
S T = S T

9. Inversas de transformaciones lineales
 Definición :
Sean S yT transformaciones
lineales de Rn a Rm. Entonces S yT son
“transformaciones inversas” si ocurre
que S T = In y T S = In.

10. Inversas de transformaciones lineales
 TEOREMA 4
Sea T: Rn Rn una matriz
invertible. Entonces su matriz estándar T
es una matriz invertible, y
T-1 = T -1

11. Asociatividad
 Sean R = TA, S = TB y T = TC.
 A(BC) = (AB)C si y solo si R (S T) = (R S) T
 (R (S T))(x) = R((S T)(x))
= R(S(T(x)))
= (R S)(T(x)) = ((R S) T)(x)

12. Muchas de las transformaciones lineales que hemos estudiado,
conservan la forma y las medidas de las figuras u objetos, como por
ejemplo las simetrías y las rotaciones.

14. Integrantes:
Taboada Laura Ornella
Del Rio Candela
Cortez Julio Ricardo
Palacio Eliana Jessica
Frojel Rita María E.
Gramajo Silvia Alejandra
Fuentes Claudia Andrea