El documento describe un modelo matemático de la suspensión de un automóvil usando ecuaciones diferenciales. Se modela la suspensión como un sistema masa-resorte-amortiguador donde la masa representa el chasis, el resorte la constante elástica y el amortiguador el coeficiente de fricción. Se aplica la transformada de Laplace para obtener la función de transferencia del sistema y simular su comportamiento.

1. Aplicación Laplace
Sistema masa amortiguador
Ecuaciones Diferenciales
Suspensión de un
automóvil

2. • La Transformada de Laplace es una técnica
Matemática que forma parte de ciertas
transformadas integrales como la transformada de
Fourier
•el comportamiento de sistemas complejos puede
describirse usando ecuaciones algebraicas en
lugar de ecuaciones diferenciales.
•Una vez que se ha estudiado el comportamiento
de los sistemas, se puede proceder analizar los
Introducción

3. Suspensión automóvil
 La suspensión en un automóvil es el conjunto
de elementos que absorben las irregularidades
del terreno por el que se circula para aumentar
la comodidad y el control del vehículo. El
sistema de suspensión actúa entre el chasis y
las ruedas, las cuales reciben de forma directa
las irregularidades de la superficie transitada.

4. Control en automóvil
Suspensión de un
automóvil

5. MODELADO MATEMÁTICO
Suspensión de un
automóvil
f(t)
z(t)
k
b
m
Fuerza de
entrada
Desplazamiento,
salida del sistema
2
2
)()(
)()(
dt
tzd
m
dt
tdz
btkztf
maF



6. la transformada de Laplace
Ahora pasamos al modelado del
sistema, por la ley de Newton
tenemos que:
𝐹 = 𝑚𝑎
Entonces decimos que: F(t) = m𝑋2+ b 𝑋1 + kX(t)
Ahora aplicando la transformada de Laplace a
la expresión anterior se tiene:
F(s) = m 𝑆2
X(s) + bSX(s) + kX(s)
Despejando X(s):
F(s) = X(s)[m𝑆2 + bS + k]

7. Obteniendo la relación de la transformada de
Laplace de la salida respecto a la entrada, que
corresponde a la función de transferencia del
sistema se obtiene:
X(s)
F(s)
=
1
m 𝑆2+bS+k
Ahora normalizando la ecuación para dejarla
expresada como función de transferencia se
tiene:
𝐹𝑇 =
X(s)
F(s)
=
1
𝑚
𝑆2+ 𝑏
𝑚
S+ 𝑘
𝑚
Ecuación de
modelar el
sistema.

8. Programa.
Parámetros del
sistema
Se tiene el siguiente sistema que
simula el funcionamiento de la
suspensión donde:
m es la masa del chasis del vehículo.
k es la constante elástica del resorte
o muelle.
b es el coeficiente de fricción del
amortiguador.

9. Interfaz

10. Ya dependiendo de los valores
de B, M y K que ingresemos en
la interfaz grafica.
Podremos tener diferentes
respuestas

11. EJEMPLO
 Consideremos un sistema masa-resorte con m = 2
kg, c = 4 Nm/s y k =10 N/m. Supongamos que el
sistema está inicialmente en reposo y en equilibrio
por lo cual x.(0)= x’(0) = 0, y que la masa es
impulsada por una fuerza de excitación f(t) cuya
gráfica se muestra en la figura siguiente.

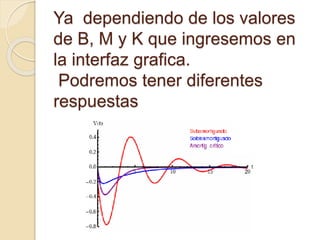
12. La posición x.(t) de la masa m está dada por
la solución del PVI:
2x’’(t) + 4x’(t) + 10x(t)
f(t)=
10, si π ≤ t <−2π 𝑐𝑜𝑛 𝑥 0 =
0, si t[π , 2 π ) 𝑥′
0 = 0
La función f (t) puede escribirse como
f(t)= -10 [u( t - π ) -u(t-2 π )]•; entonces por la
linealidad de la T Laplace
tenemos:
F(s)= ℒ{f(t)} =
10𝑒−2π 𝑆
𝑆
−
10𝑒−π 𝑆
𝑆
.
Ahora, tomamos TL en ambos miembros de
la ED para obtener:

13. 2[𝑆2
X(S) – SX(0) – x’(0)] +4[SX(S)-X(0)] +
10X(S) =F(S)
Al considerar las condiciones iniciales y la
expresión de F(S), tenemos que:
2𝑆2X(S)+4SX(S)+ 10X(S) =
10𝑒−2π 𝑆
𝑆
−
10𝑒−π 𝑆
𝑆
2(𝑆2
+2S + 5)X(S) =
10𝑒−2π 𝑆
𝑆
−
10𝑒−π 𝑆
𝑆
X(S) =
5𝑒−2π 𝑆
𝑆(𝑆2 +2S + 5)
−
5𝑒−π 𝑆
𝑆(𝑆2 +2S + 5)

14. Por lo tanto, para encontrar x(t), lo único
que resta es obtener la transformada
inversa de Laplace.
En primer lugar, por la primera propiedad
de traslación, se tiene que
ℒ−1
{
1
𝑆(𝑆2 +2S + 5)
} = ℒ−1
{
1
(𝑆+1)2 + 4)
} =
1
2
ℒ−1
{
1
(𝑆+1)2 + 4)
} =
1
2
𝑒−1
sen2t.
Luego, calculamos ℒ−1
{
1
𝑆(𝑆2 +2S + 5)
}
Utilizando la propiedad de la
transformada de una integral

15. ℒ−1
{
1
𝑆(𝑆2 +2S + 5)
} = 0
𝑡 1
2
𝑒−𝑢
𝑠𝑒𝑛2𝑢𝑑𝑢
=
1
2
[ 𝑒−𝑢
(2𝑐𝑜𝑠2𝑢 + 𝑠𝑒𝑛2𝑢]
𝑡
𝑜
=
=
1
5
−
1
10
[ 𝑒−𝑡
2𝑐𝑜𝑠2𝑡 + 𝑠𝑒𝑛2𝑡 .
Finalmente, al utilizar la segunda
propiedad de traslación y la periodicidad
de las funciones seno y coseno, se
determina que
X(t) = 5ℒ−1 𝑒−2π𝑠
𝑆(𝑆2 +2S + 5)
-
5ℒ−1 𝑒−π𝑠
𝑆(𝑆2 +2S + 5)
=

16. = 1 −
1
2
𝑒− 𝑡−2𝜋 [2 cos 2𝑡 − 4𝜋 + 𝑠𝑒𝑛(2𝑡 −

17. Grafiacas del ejercio vs la de matlab