1) Se debe tener cuidado al sumar o restar variables afectadas por operadores trigonométricos, ya que no es como sumar o multiplicar variables algebraicas comunes. 2) Para sumas y diferencias de variables trigonométricas existen fórmulas especiales que se presentarán en este capítulo. 3) El objetivo es aprender a aplicar correctamente estas fórmulas especiales para simplificar expresiones que involucren la suma o diferencia de variables trigonométricas.

1. UNIDAD VIII
Sumando y restando variables
Debemos tener mucho cuidado al operar sumas en variables afectadas por operadores trigonométricos
puesto que no es como sumar o multiplicar cualquier variable algebraica, por ejemplo es fácil operar esto:
A(X + Y) = A . X + A . Y; pero en variables afectadas por operadores trigonométricos no es posible esto:
sen(X + Y) = sen X + senY, esta operación es incorrecta puesto que el operador "sen" indica una determinada
operación a realizar que no es la multiplicación por sus variables, así en este capítulo encontraremos
fórmulas especiales para este tipo de expresiones.
Comunicación matemática
• Identificar la aplicación de fórmulas espe-
ciales para suma de variables.
Análisis y demostración
• Demostrar expresiones de sumas y dife-
rencia de variables.
Resolución de problemas
• Resolver problemas de simplificación so-
bre suma y diferencia de variables.
D
H

2. 136
Sistemas de medición angular
TRILCE
Colegios
www.trilce.edu.pe
Identidades de la suma y
diferencia de variables I
Conceptos básicos
Fórmulas básicas
1. Para la suma de variables
sen(x + y) = senx . cosy + seny . cosx
cos(x + y)=cosx . cosy – senx . seny
tan(x + y) =
tanx + tany
1 – tanx . tany
Ejemplos:
Completa las fórmulas siguientes:
• sen(a + b) = sena . cosb + • sen(70° + a) = sen70° . cosa +
• cos(20° + a) = cos20° . cosa – • cos(a + 10°) =
•
tan(a + 10°) = tana +
1 –
• tan(45° + b) =
2. Para la diferencia de variables
sen(x – y) = senx . cosy – seny . cosx
cos(x – y)=cosx . cosy + senx . seny
tan(x – y) =
tanx – tany
1 + tanx . tany
Ejemplos:
Completa las fórmulas siguientes:
• sen(a – b) = sena . cosb – • sen(20° – q) =
• cos(70° – x) = cos70° . cosx + • cos(30° – x) = cos30° . cosx +
•
tan(x – 20°) =
• tan(60° – b) = __________________
Problemas resueltos
1. Demostrar que:
sen(a – b)
cosa . cosb
= tana – tanb
Resolución:
Desarrollando en el primer miembro:
sen(a – b)
cosa . cosb
= tana – tanb ⇒
sena . cosb – senb . cosa
cosa . cosb
= tana – tanb

3. Razonamiento Matemático
137
1
Trigonometría
Unidad I
Central: 619-8100
Desdoblando en fracciones homogéneas:
sena . cosb
cosa . cosb
–
senb . cosa
cosa . cosb
= tana – tanb
Reduciendo:
sena
cosa
–
senb
cosb
= tana – tanb
123 123
demostrado: tana – tanb = tana – tanb
2. Reducir: C = cos(60° + x) + cos(60° – x)
Resolución:
Desarrollando los dos miembros:
C = cos(60° + x) + cos(60° – x) = cos60° . cosx – sen60° . senx + cos60° . cosx + sen60° . senx
Reduciendo:
C = 2cos60° . cosx → pero: cos60° =
1
2
C = 2
1
2
. cosx ⇒ C = cosx
3. Reducir: C = tana + tanb + tana . tanb; si: a + b = 45°
Resolución:
Como: a + b = 45°
⇒ tan(a + b) = tan45°
Desarrollando:
tana + tanb
1 – tana . tanb
= 1 → tana + tanb = 1 – tana . tanb
Trasladando términos:
tana + tanb + tana . tanb = 1 ⇒ C = 1
4. Siendo: sena = 3
10
∧ senq = 2
5
("a" y "q" agudos), calcular: tan(a – q)
Resolución:
Como:
sena = 3
10
10 3
1
a
⇒ tana = 3 senq = 2
5
5 2
1
q
⇒ tanq = 2
Entonces: tan(a – q) =
tana – tanq
1 + tana . tanq
⇒ tan(a – q) =
3 – 2
1 + 3 . 2
⇒ tan(a – q) =
1
7
5. Del gráfico mostrado, calcular "tanq".
A B
D C
1
5
4
q

4. 138
Sistemas de medición angular
TRILCE
Colegios
www.trilce.edu.pe
Resolución:
Del gráfico:
A B
D C
1
5
4
q
x
y
Sea: ABD = x; ACD = y
Luego: q = x + y ... (prop. geométrica)
tanq = tan(x + y) ⇒ tanq =
tanx + tany
1 – tanx . tany
.
...... (1)
DAB: tanx = 4
ADC: tany =
4
5
En(1): tanq =
4 +
4
5
1 – 4 .
4
5
=
24
5
–
11
5
⇒ tanq = –
24
11
Aplica lo comprendido
10 x
5
50
1. Reducir: M =
sen(x + y) – senx . cosy
cosx . cosy
2. Si: tanx = 5 ∧ tany=3, calcular: tan(x – y)
3. Simplificar:
E = sen20° . cos25° + sen25° . cos20°
4. ¿A qué es igual:
P = cos40°. cos20° – sen40°. sen20° ?
5. Reducir: M =
sen4x – cos3x . senx
sen3x
Aprende más...
1. Reducir:
P =
sen(a + b) – senb . cosa
cosa . cosb
a) tanb b) tana c) cota
d) cotb e) 1
2. Reducir:
M =
sen(a – q) + senq . cosa
cos(a – q) – cosa . cosq
a) tanb b) tanq c) cota
d) cotq e) 1
3. Reducir:
J =
cos(45° + x) + cos(45° – x)
senx
a) 2 b) 2 2 c) cotx
d) 2cotx e) 2 2cotx
4. Si: senx + cosx = 3
4
, calcular:
A = sen(45° + x)
a)
6
2
b)
6
4
c)
3
4
d)
3
8
e)
6
8
5. Si: senx – 3cosx =
1
4
Calcular: A = sen(x – 60°)
a)
3
8
b)
3
4
c)
1
4
d)
1
2
e)
1
8
6. Reducir: J =
sen(x + y)
cosx . cosy
+
sen(z – x)
cosz . cosx
a) tanx b) tanz c) tany
d) tanz – tany e) tanz+tany

5. Razonamiento Matemático
139
1
Trigonometría
Unidad I
Central: 619-8100
7. Reducir:
J =
sen(x – y)
cosx . cosy
+
sen(y – z)
cosy . cosz
+
sen(z – x)
cosz . cosx
a) 1 b) 2
c) 0 d) tanx + tany + tanz
e) tanx . tany . tanz
8. Simplificar
A =
sen5x . cos3x – sen3x . cos5x
cos4x . cos2x + sen4x . sen2x
a) tanx b) tan2x c) 1
d) tan3x e) tan5x
9. Simplificar:
A =
cos7x . cos4x + sen7x . sen4x
sen4x . cosx – senx . cos4x
a) cotx b) tanx c) cot3x
d) tan3x e) 1
10. Si "a" y "b" son ángulos agudos; tales que:
csca = 10 ∧ cscb = 13
2
, calcular: tan(a + b)
a)
7
9
b)
5
9
c)
9
5
d)
9
7
e)
4
3
11. Si "a" y "b" son ángulos agudos; tales que:
seca = 5 ∧ secb = 17
Calcular: tan(b – a)
a)
1
9
b)
1
3
c)
2
9
d)
4
9
e)
5
9
12. Si: sen(x + y) = 3sen(x – y)
Calcular: C = tanx . coty
a) 1 b) 2 c) 3
d)
1
2
e)
1
3
13. Si: cos(x – y) = 4cos(x + y)
Calcular: C = tanx . tany
a) 0,2 b) 0,4 c) 0,6
d) 0,7 e) 0,8
14. Del gráfico, calcular "tanf"
B C
D
A
E
2
5 1
f
a)
5
13
b)
9
13
c)
11
13
d)
12
13
e)
7
13
15. Del gráfico, calcular "tanf", si: AB = 6 y BC = 4
A B
C
N
M
f
a)
9
13
b)
5
13
c)
6
13
d)
7
13
e)
8
13
16. Del gráfico, calcular "tanf", si ABCD es un cuadra-
do: BQ = QN; BN = NC ; AP = 3PD y AM=MB
B
Q N
C
D
A
M
P
f
a) 3 b) – 3 c) 5
d) – 2 e)
5
3
17. Del gráfico, calcular "tana", si ABCD es un cua-
drado y además: BC = 3CE.
B
C
E
F
D
A
a
a)
121
37
b)
81
37
c)
136
31
d)
141
37
e)
156
37

6. 140
Sistemas de medición angular
TRILCE
Colegios
www.trilce.edu.pe
¡Tú puedes!
1. Siendo: senx + seny = senz
cosx + cosy = cosz
Calcular: cos(x – y)
a)
1
2
b)
3
2
c)
–
1
2
d)
– 3
2
e)
– 2
2
2. Sabiendo que:
5
S senqi = 0
i = 1
;
5
S cosqi = 0
i = 1
, determine: C =
5
S sen(qi + x)
i = 1
+
5
S cos(qi + x)
i = 1
a) 2 b) –1 c) 0 d)
1
2
e) –
1
2
3. En el gráfico mostrado, hallar el área del trapecio ABCD.
a) sen(q + a) . sen(q – a) b) cos(q + a) . cos(q – a)
c) sen(q + a) . cos(q – a) d) sen(q – a) . cos(q + a)
e) 2sen(q + a) . cos(q – a)
B
P
C
D
A
2
a q
4. Si: x + y + z = 90°, hallar el equivalente de: T = (cotx – tany)(coty – tanx)(cotx – tanz)
a) senx . seny . senz b) cosx . cosy . cosz c) cscx . cscy . cscz
d) secx . secy . secz e) – secx . secy . secz
5. En la circunferencia trigonométrica mostrada, hallar la distancia entre
"M" y "N"
a) vers(a – b) b)
cov(a – b) c)
2vers(a – b)
d) 2cov(a – b) e) 2 vers(a – b)
A'
B
A
B'
O
Y
X
M
N
a
b
Practica en casa
18:10:45
1. Reducir: A=
sen(a + b) – senb . cosa
sena . senb
2. Reducir: P=
cos(a + b) + senb . sena
sena . cosb
3. Demostrar que: sen(45° + x) = 2
2
(senx + cosx)
4. Reducir: M=
cos(60° + x) + cos(60° – x)
senx
5. Simplificar: C =
sen(x + y)
cosx . cosy
– tanx
6. Reducir: C =
cos(x – y)
senx . cosy
– cotx

7. Razonamiento Matemático
141
1
Trigonometría
Unidad I
Central: 619-8100
7. Reducir la expresión:
M =
sen40°.cos20° + cos40°.sen20°
cos20°.cos10° – sen20°.sen10°
8. Si: sen(a + b) = 4sen(a – b)
Calcular: Q =
tana
tanb
9. Sabiendo que "a" y "q" son agudos, tales que:
cosa =
2
29
∧ cosq =
2
13
, calcular: tan(a + q)
10. Sabiendo que "a" y "b" son agudos, tales que:
sena =
3
13
∧ senb =
1
5
, calcular: tan(a – b)
11. Del gráfico, calcular "tanq".
A
5 6
N
B
M
C
2
2
q
12. Si: x + y = 45° ∧ tanx=
1
6
, calcular: tany
13. Si: ABCD es un cuadrado, hallar "tanq"
q
A B
D C
P Q
2 3
1
14. Calcular: Q = tan50°
tan70° – tan20°
+ 1
15. Si: tan(a + b + c) = 5 y tan(a + b) = 3
Calcular: cot(45° + c)

8. 142
Sistemas de medición angular
TRILCE
Colegios
www.trilce.edu.pe
142
Identidades de la suma y diferencia de variables II
TRILCE
Colegios
www.trilce.edu.pe
Identidades de la suma y
diferencia de variables II
Conceptos básicos
Propiedades
I. Si: K = A senx ± Bcosx ⇒
Kmáx = A2 + B2
Kmín = – A2 + B2
Ejemplos:
• E = 3senx + 4cosx ⇒
Emáx = 32 + 42 = 5
Emín = – 32 + 42 = – 5
• E = 2senx – cosx ⇒
Emáx =
Emín =
II. tana + tanb + tana . tanb . tan(a + b) = tan(a + b)
III. tana – tanb – tana . tanb . tan(a – b) = tan(a – b)
Ejemplos:
• tan12° + tan14° + tan12° . tan14° . tan26° = tan26°
123
12° + 14°
• tan20° + tan40° + 3 . tan20° . tan40° = ??
Note que: 3 =tan60°, luego la expresión sería: tan20° + tan40° + tan20° . tan40° . 3
123
tan60°
tan20° + tan40° + tan20° . tan40° . tan60° = tan60°= 3
123
20º + 40°
IV. Si: a + b + q = np ó 180° . n; n ∈ ⇒
tana + tanb + tanq = tana . tanb . tanq
cota . cotb + cotb . cotq + cotq . cota = 1
Ejemplos:
• tan40° + tan80° + tan60° = tan40° . tan80° . tan60° (ya que: 40° + 80° + 60° = 180°)
• tan34° + tan66° + tan80° =
• cot20° . cot60° + cot60° . cot100° + cot100° . cot20° = 1 (ya que: 20°+60°+100°=180°)
• cot50° . cot70° + cot70° . cot60° + cot60° . cot50° =

9. Razonamiento Matemático
143
1
Trigonometría
Unidad I
Central: 619-8100
Razonamiento Matemático
143
2
Trigonometría
Unidad VIII
Central: 619-8100
V. Si: a + b + q = (2n + 1)p
2
ó (2n + 1) . 90°; n ∈ ⇒
cota + cotb + cotq = cota . cotb . cotq
tana . tanb + tanb . tanq + tanq . tana = 1
Ejemplos:
• cot20° + cot60° + cot10° = cot20° . cot60°. cot10° (ya que: 20° + 60° + 10° = 90°)
• tan20° . tan42° + tan42° . tan28° + tan28° . tan20° = 1 (ya que: 20° + 42° + 28° = 90°)
Síntesis teórica

10. 144
Sistemas de medición angular
TRILCE
Colegios
www.trilce.edu.pe
144
Identidades de la suma y diferencia de variables II
TRILCE
Colegios
www.trilce.edu.pe
Problemas resueltos
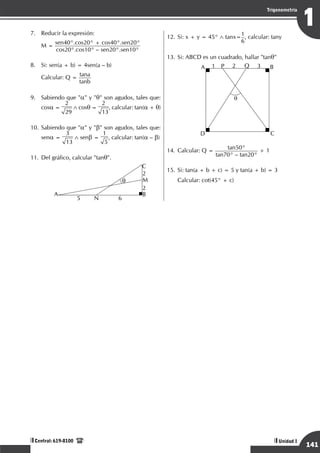
1. Calcular la suma del máximo valor de: C = 3senx + 4cosx + 5, con el mínimo valor de:
L = senx + 3cosx + 1
a) 3 b) 7 c) 9 d) 11 e) 12
Resolución:
Analizando cada expresión:
I. C = 3senx + 4cosx + 5, para que: C: máx ⇒ a: máx
1442443
a
como: a = 3senx + 4cosx ⇒ amáx = 32 + 42 = 5, luego: Cmáx = 5 + 5 ⇒ Cmáx = 10
II. L = senx + 3cosx + 1, para que: L : mín ⇒ b: mín
1442443
b
como: b = 1 . senx + 3cosx ⇒ bmín = – 12 + 32
= – 2
Luego: Lmín = – 2 + 1 ⇒ Lmín = – 1
III. Piden calcular: Cmáx + Lmín = 10 + (–1) ⇒ Cmáx + Lmín = 9
2. Señale la variación de: L = 2 2sen(x + 45°) + senx + 2cosx + 1
a) [– 1; 3] b) [– 2; 4] c) [– 3; 5] d) [– 4; 6] e) [– 5; 5]
Resolución:
En este caso, primero, desarrollaremos la expresión:
L = 2 2sen(x + 45°) + senx + 2cosx + 1
L = 2 2(senx. cos45° + sen45° . cosx) + senx + 2cosx + 1
L = 2 2 senx .
1
2
+
1
2
. cosx + senx + 2cosx + 1
Reduciendo:
L = 2senx + 2cosx + senx + 2cosx + 1 ⇒ L = 3senx + 4cosx + 1
Pero, note que: 3senx + 4 cosx
máx = 5
mín = – 5
⇒
Lmáx = 5 + 1 = 6
Lmín = – 5 + 1 = – 4
⇒ L ∈ [–4; 6]
3. Reducir: L = tan34° + tan26° + 3tan34° . tan26°
tan33° + tan12° + tan33° . tan12°
a) 1 b) 3 c)
3
3
d) 2 e) 2 3
Resolución:
En el numerador:
tan34° + tan26° + 3tan34° . tan26°= tan34° + tan26° + tan34° . tan26° . tan60° = tan60°= 3
En el denominador:
tan33° + tan12° + 1 . tan33° . tan12° = tan33° + tan12° + tan33° . tan12° . tan45° = tan45° = 1

11. Razonamiento Matemático
145
1
Trigonometría
Unidad I
Central: 619-8100
Razonamiento Matemático
145
2
Trigonometría
Unidad VIII
Central: 619-8100
En la expresión:
L = tan34° + tan26° + 3tan34° . tan26°
tan33° + tan12° + tan33° . tan12°
⇒ L = 3
1
⇒ L = 3
4. En un triángulo ABC: tanA = 2 y tanB = 4. Calcular "tanC"
a)
3
7
b)
5
6
c)
3
4
d)
6
7
e)
2
3
Resolución:
Como en un triángulo ABC: A + B + C = 180°, se cumple:
tanA + tanB + tanC = tanA . tanB . tanC (tanA = 2 y tanB = 4)
Reemplazando: 2 + 4 + tanC = 2 . 4 . tanC
6 + tanC = 8tanC ⇒ 6 = 7tanC ⇒ tanC =
6
7
5. En un triángulo ABC: tanA + tanB = 5tanC. Calcular: L = tanA . tanB
a) 5 b) 6 c) 7 d) 10 e) 15
Resolución:
Como en un triángulo ABC: A + B + C = 180°
Se cumple: tanA + tanB + tanC = tanA . tanB . tanC
14243 14243
5tanC L
Luego: 5tanC + tanC = L . tanC ⇒ 6tanC = L . tanC ⇒ L = 6
Aplica lo comprendido
10 x
5
50
1. Indicar si es verdadero "V" o falso "F"
• tan5x + tan10x + tan5x . tan10x . tan15x = tan 30x ( )
• tan20° + tan40° + 3 . tan20° . tan40° = 3 ( )
2. Indicar si es verdadero "V" o falso "F"
a) El máximo valor de: E = 2 senx – 7cosx; es 3 ( )
b) El máximo valor de: E = 3sen20° + 4 cos20°; es 5 ( )
3. El mínimo valor de: Q = 5senx + 12cosx + 3; es:
4. En un triángulo ABC, reducir: K =
tanA + tanB + tanC
tanB . tanC
5. Simplificar: U =
cot20° + cot60° + cot10°
cot20° . cot10°

12. 146
Sistemas de medición angular
TRILCE
Colegios
www.trilce.edu.pe
146
Identidades de la suma y diferencia de variables II
TRILCE
Colegios
www.trilce.edu.pe
Aprende más...
1. Señale el máximo valor de: H = 3senx – 2cosx
a) 13 b)
7 c)
11
d) 15 e)
17
2. Hallar la suma del máximo y mínimo valor de:
Q = 3senx – 4cosx + 2
a) 6 b) – 4 c) 10
d) – 2 e) 4
3. Señale el máximo valor de:
A = 2sen(x + 30°) + 3cosx
a) 17 b) 4 c) 3
d) 19 e)
21
4. Señale la variación de: E = 5senx – 12cosx + 1
a) [– 12; 13] b) [– 14; 14] c) [– 12; 14]
d) [– 11; 13] e) [– 13; 13]
5. Reducir:
C =
tan10° + tan12° + tan10° . tan12° . tan22°
tan15° + tan7° + tan15° . tan7° . tan22°
a) 1 b) 2 c) tan15°
d) tan222° e) 2tan22°
6. Señale un valor agudo de "x", si:
tan2x + tan3x + tan2x . tan3x . tan5x =
1
2
sec5x
a) 2° b) 4° c) 6°
d) 10° e) 12°
7. En un triángulo ABC: tanA = 3 y tanB = 4.
Calcular "tanC"
a)
5
7
b)
7
11
c)
6
11
d)
8
11
e)
4
9
8. En un triángulo ABC: tanA = 4 y tanC = 5. Cal-
cular "tanB"
a)
9
20
b)
9
19
c)
9
7
d)
7
20
e)
7
19
9. En un triángulo ABC; se cumple:
tanA + tanB + tanC = 7tanC
Calcular: tanA . tanB
a) 7 b) 6 c) 5
d) 4 e) 3
10. En un triángulo ABC:
cotA . cotB =
1
4
; cotB . cotC =
1
5
Calcular: P = cotA . cotC
a)
11
15
b)
7
15
c)
7
20
d)
11
20
e)
13
20
11. En un triángulo ABC, reducir:
K =
cotA + tanB
tanB
+
cotB + 3tanC
tanC
+
cotC + 2tanA
tanA
a) 5 b) 6 c) 7
d) 8 e) 10
12. Si: x + y + z = 180°, calcular:
tgy
ctgx tgy
tgz
ctgy tgz
tgx
ctgz tgx
7 6 5
+
+
+
+
+
a) 17 b) 18 c) 19
d) 21 e) 12
13. Si: x + y + z = 90°; tana = tanx + tany + tanz
Hallar: L = sec2x + sec2y + sec2z
a) tan2a b) seca c) sec2a
d) tan2a + 2 e) tan2a – 1
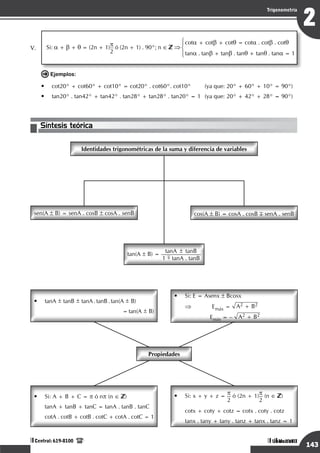
14. Del gráfico, calcular "tanq"
A C
D E
B
2
3
1
37º
q
a)
20
3
b)
29
15
c)
29
45
d)
3
29
e)
108
77
15. En un triángulo acutángulo ABC; reducir:
L = csc2A + csc2B + csc2C – 1
a) tanA + tanB + tanC
b) cotA + cotB + cotC
c) tanA . tanB . tanC
d) cotA . cotB . cotC
e) cscA . cscB . cscC

13. Razonamiento Matemático
147
1
Trigonometría
Unidad I
Central: 619-8100
Razonamiento Matemático
147
2
Trigonometría
Unidad VIII
Central: 619-8100
1. En un triángulo ABC, calcular: K =
tanA + cotB
tanA
+
tanB + cotC
tanB
+
tanC + cotA
tanC
a) 1 b) 2 c) 3 d) 4 e) 5
2. Señale el máximo valor de: A = a(senx – cosx) + b 2cos(45° – x)
a) 2 a2 + b2 b)
2(a2 + b2) c)
a2 + b2 d) 3 a2 + b2 e)
2ab
3. Si: x + y + z = p, determine el equivalente de: M=(cotx + coty)(coty + cotz)(cotz + cotx)
a) secx . secy . secz b) – secx . secy . secz c) cscx . cscy . cscz
d) – cscx . cscy . cscz e) – senx . seny . senz
4. En el gráfico, calcular: K = a2 + b2 + c2 + abc
a) 2 b) 3 c) 4
d) 8 e) 6
A
B
C
D
O
b
a
c
1
5. Si: a + b + q = 90°, calcular: L =
cos(a – b)
cosa . cosb
+
cos(b – q)
cosb . cosq
+
cos(q – a)
cosq . cosa
a) 1 b) 2 c) 3 d) 4 e) 5
1. Indicar V ó F, según corresponda:
I. El máximo valor de:
13senx + 3cosx, es 4 ( )
II. El mínimo valor de:
12 senx – 5cosx, es –7 ( )
III. El máximo valor de:
7senx + 2cosx, es 3 ( )
2. Señale el máximo valor de:
G = 2sen(x + 45°) + senx
3. Determinar el máximo valor de:
E = 3cos(60° + x) + 3senx
4. En un triángulo ABC, reducir:
P = (tanA + tanB + tanC) . cotA . cotB . cotC
¡Tú puedes!
Practica en casa
18:10:45
5. Reducir:
tan13° . tan27° + tan27°.tan50° + tan13°.tan50°
6. En un triángulo ABC, si: 2tanA + 2tanB = 3tanC
Calcular: E = tanA . tanB
7. Si: x + y + z = p
2
; además: cotx + coty = 2cotz
Calcular: P = cotx . coty
8. Reducir:
E = tan7x + tan2x + tan9x . tan7x . tan2x
9. Calcular:
E = tan20° + tan40° + 3tan20° . tan40°
10. Calcular: E = ( 3 + tan10°)( 3 + tan20°)