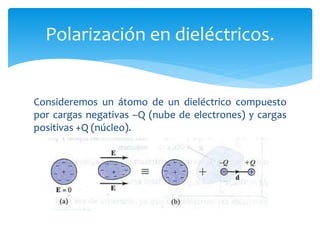
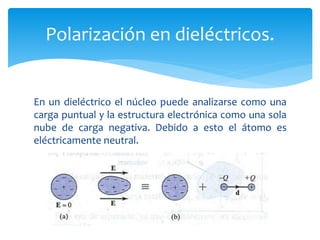
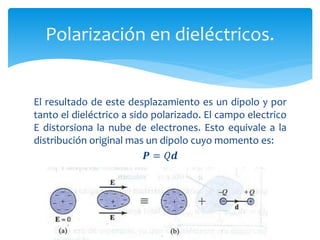
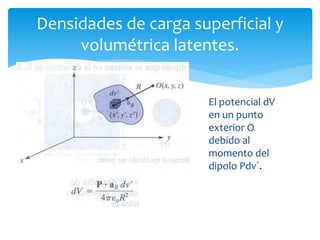
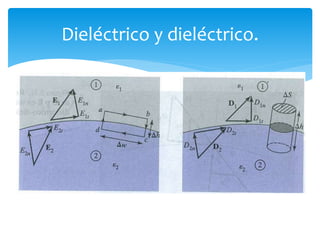
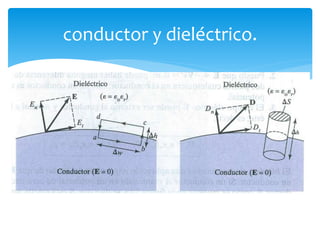
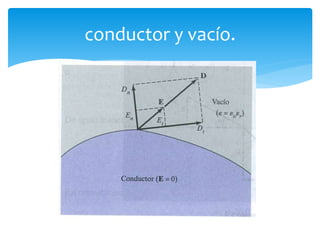
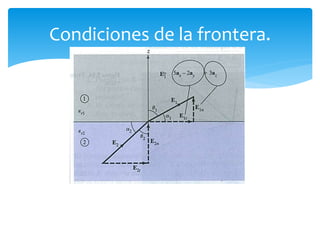
La unidad 2 del documento trata sobre el campo eléctrico estático en dieléctricos, explicando la conductividad eléctrica y la polarización de materiales dieléctricos. Se detallan las diferencias entre dieléctricos polares y no polares, así como conceptos de densidades de carga y condiciones en la frontera entre diferentes medios. Además, se introducen parámetros como la constante dieléctrica y las características de materiales dieléctricos lineales, isotrópicos y homogéneos.

1. UNIDAD 2: CAMPO ELECTRICO
ESTATICO EN DIELECTRICOS.
TEORIA DE CAMPO ELECTROMAGNETICO.

2. La conductividad eléctrica es la medida de la capacidad
de un material o sustancia para dejar pasar la corriente
eléctrica a través de él. La conductividad depende de la
estructura atómica y molecular del material. y su unidad
es el S/m (siemens por metro)
Conductividad.

3. Conductividad.

4. Consideremos un átomo de un dieléctrico compuesto
por cargas negativas –Q (nube de electrones) y cargas
positivas +Q (núcleo).
Polarización en dieléctricos.

5. En un dieléctrico el núcleo puede analizarse como una
carga puntual y la estructura electrónica como una sola
nube de carga negativa. Debido a esto el átomo es
eléctricamente neutral.
Polarización en dieléctricos.

6. Si se aplica un campo electrico E, la carga positiva se
desplaza por la fuerza 𝑭+ = 𝑄𝑬 desde su posición de
equilibrio hacia la dirección de E. la carga negativa es
desplazada en dirección opuesta por la fuerza 𝑭− = 𝑄𝑬
Polarización en dieléctricos.

7. El resultado de este desplazamiento es un dipolo y por
tanto el dieléctrico a sido polarizado. El campo electrico
E distorsiona la nube de electrones. Esto equivale a la
distribución original mas un dipolo cuyo momento es:
𝑷 = 𝑄𝒅
Polarización en dieléctricos.

8. Si hay N dipolos contenidos en cierto volumen Δv de un
dieléctrico el momento del dipolo total puede
expresarse de la siguiente manera:
Polarización en dieléctricos.

9. La polarización P en C/m2 es el momento del dipolo por
unidad de volumen en un dieléctrico:
Polarización en dieléctricos.

10. “los dieléctricos no polares son aquellos materiales en
los que no hay presencia de dipolos hasta que en
determinado momento se aplica un campo electrico”
Ejemplos: hidrogeno, el oxigeno, nitrógeno y gases
enrarecidos.
Dieléctricos polares y no polares.

11. “los dieléctricos polares
poseen dipolos
permanentes integrados
de una manera aleatoria”
En este tipo de dieléctricos
al someterlos a la acción
de un campo electrico los
dipolos tienden a alinearse
con la direccion del campo
electrico.
Dieléctricos polares y no polares.

12. Densidades de carga superficial y
volumétrica latentes.
El potencial dV
en un punto
exterior O
debido al
momento del
dipolo Pdv´.

13. Densidades de carga superficial y
volumétrica latentes.
R es el vector de
posición del
punto O.
obtenemos el
gradiente de R
Para operar el
dV.

14. Densidades de carga superficial y
volumétrica latentes.
Utilizando esta identidad
vectorial obtenemos una
expresión para el
momento del dipolo y
luego sustituimos en el
dV.

15. Densidades de carga superficial y
volumétrica latentes.
De la expresión de V
obtenemos las
densidades de carga
superficial y volumétrica
latentes. Podemos
encontrar la carga
latente positiva en la
superficie mientras que
también podemos
encontrar la carga que
permanece dentro de la
superficie .

16. Densidades de carga superficial y
volumétrica latentes.
Si consideramos carga
libre en el dieléctrico
podemos encontrar la
densidad volumétrica
total y la densidad de
flujo electrico.
D se ve incrementada en
el dieléctrico debido a la
polarización P.

17. Densidades de carga superficial y
volumétrica latentes.
Para algunos dieléctricos
la polarización se puede
encontrar utilizando el
valor de susceptibilidad
electrica del material.

18. Constante dieléctrica.
*ε es la permitividad del
dieléctrico.
*ε0 es la permitividad del
vacío.
* Εr es la constante
dieléctrica o permitividad
relativa.
“la constante dieléctrica es
la razón de la permitividad
del dieléctrico al vacío.”

19. Dieléctricos lineales, isotrópicos y
homogéneos.
“un material dieléctrico es lineal si D varia linealmente
con E, y es no lineal en el caso contrario”.
“un material es dieléctrico homogéneo cuando ε (la
permitividad) o σ (la conductancia) no varían en la
región de consideración, sino que es igual en todos los
puntos (no depende de x,y,z), es inhomogeneo en el
caso que depende de x,y,z.”

20. Dieléctricos lineales, isotrópicos y
homogéneos.
“un material dieléctrico es isotrópico cuando D y E
siguen la misma direccion. Es aniso trópico cuando D, E
y P no son paralelos.”

21. Dieléctricos lineales, isotrópicos y
homogéneos.

22. Dieléctricos lineales, isotrópicos y
homogéneos.

23. Condiciones en la frontera.
Estas condiciones se dan en regiones compuestas por dos
medios distintos y hay una interfaz que separa a ambos
medios. Las condiciones de frontera requiere que en uno de
los dos medios se encuentre un campo para encontrar el
campo en el otro medio. Se consideraran tres escenarios:
A. Dieléctrico y dieléctrico.
B. Conductor y dieléctrico
C. Conductor y vacío.

24. Dieléctrico y dieléctrico.

25. Dieléctrico y dieléctrico.

26. conductor y dieléctrico.

27. conductor y vacío.

28. Condiciones de la frontera.

29. Condiciones de la frontera.