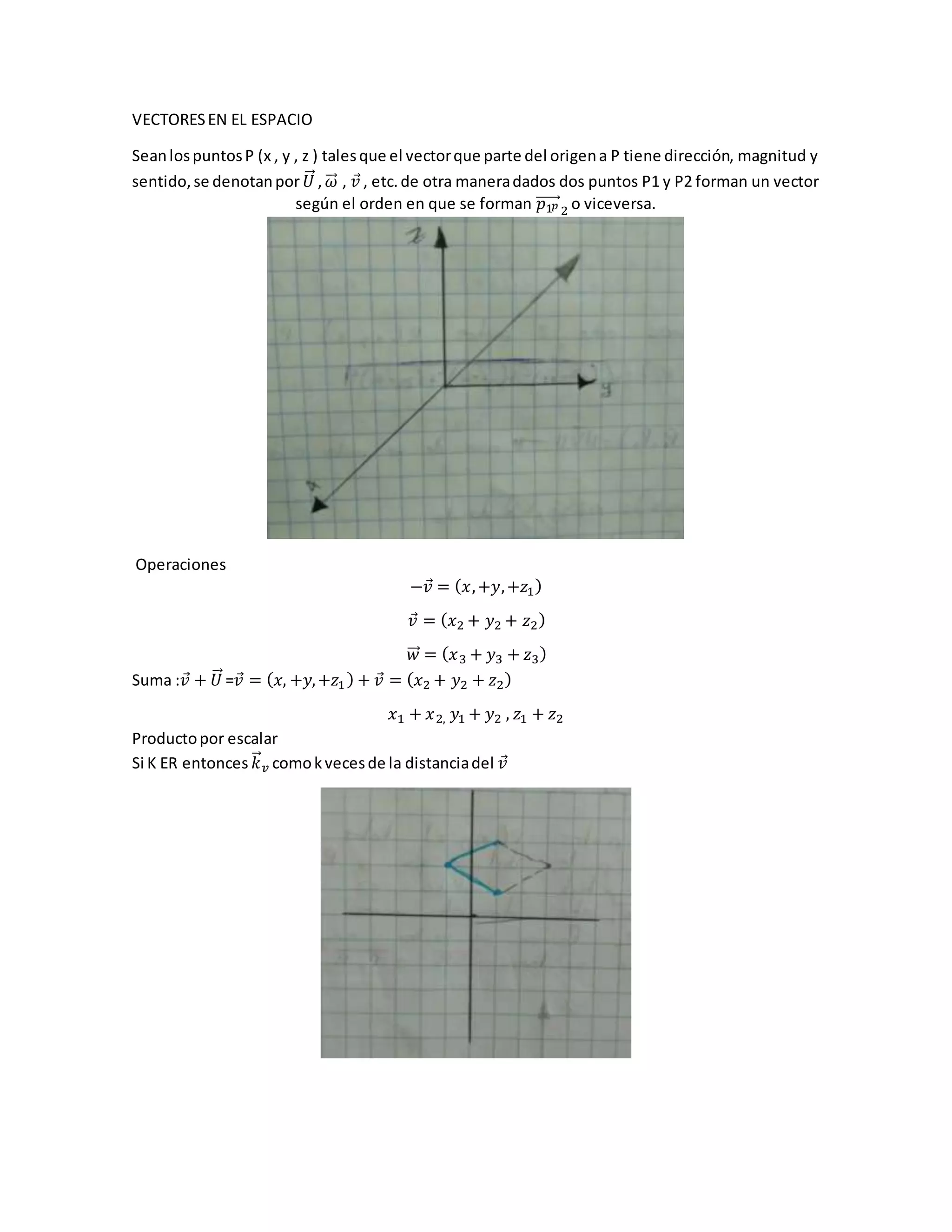
El documento describe conceptos básicos de vectores en el espacio, incluyendo su dirección, magnitud y sentido. Explica operaciones como suma, producto por escalar, distancia entre puntos, producto punto, propiedades y ángulo entre vectores. También cubre conceptos como vectores unitarios, producto vectorial y ortogonalidad.

1. VECTORESEN EL ESPACIO
SeanlospuntosP (x , y , z ) talesque el vectorque parte del origena P tiene dirección, magnitud y
sentido,se denotanpor 𝑈⃗⃗ , 𝜔⃗⃗ , 𝑣 , etc.de otra maneradados dos puntos P1 y P2 forman un vector
según el orden en que se forman 𝑝1 𝑝⃗⃗⃗⃗⃗⃗ 2 o viceversa.
Operaciones
−𝑣 = ( 𝑥,+𝑦,+𝑧1)
𝑣 = ( 𝑥2 + 𝑦2 + 𝑧2)
𝑤⃗⃗ = ( 𝑥3 + 𝑦3 + 𝑧3)
Suma :𝑣 + 𝑈⃗⃗ =𝑣 = ( 𝑥, +𝑦,+𝑧1) + 𝑣 = ( 𝑥2 + 𝑦2 + 𝑧2)
𝑥1 + 𝑥2, 𝑦1 + 𝑦2 , 𝑧1 + 𝑧2
Productopor escalar
Si K ER entonces 𝑘⃗ 𝑣 comokvecesde la distanciadel 𝑣

2. Distanciaentre 2 puntos P1 ( x1 , y1 , z1 ) P2 (x2, y2 , z2 )
√( 𝑥2−𝑥1
)
2
+ ( 𝑦2 − 𝑦1)2 + ( 𝑧2 − 𝑧1)2
U= d P1 , P2 = II𝑣II----------- normade unvectoro distancia
𝜈( x , y , z ) = 𝑥 𝑖̂, 𝑦𝐽̂,𝑧 𝐾̂donde sonlos vectoresunitariosde losejesx ,y, z para generarunvector
unitario.
U=
𝑣⃗
‖ 𝑣‖
= 𝑎1 𝐼̂ + 𝑎2𝐽̂ + 𝑎3 𝑘̂
Productopunto
Sean 𝑎 = (a1 , a2 , a3 ) 𝑏⃗ = ( b1 , b2 , b3 )
𝑎 ⋅ 𝑏⃗ = a1*b1 + a2*b2 + a3*b3 - Numero

3. Propiedades
1) a*a = | 𝑎|2 3) a*(b+C) = a1b+a*c
2) a*b = b*a 4)(ka)*b= k(a*b)=a (kb)
El Angulo entre dos vectores 𝑎 y 𝑏⃗ a*b= IIaII IIbII 𝐶𝛩𝑠𝜃̇ 𝑐𝑜𝑠−1(
𝑎𝑏
|| 𝑎|||| 𝑏||
)
Ortogonalidad
a y b sonortogonalessi ysolosi a*b =0
Productocruz o productovectorial
Si a= (a1 , a2 , a3 ) b( b1 , b2 , b3 )
𝑖̂ 𝑗̂ 𝑘̂
Entoncesa * b = a1 a2 a3 𝑖̂| a2 a3 - j a1 a3 +k a1 a2
b1 b2 b3 b2b3 b1 b3 b1 b2
=i( a2b3-b2a3 )-j ( a1b3 – b1b3 ) +k ( a1b2-b1a2 )
Vectornormal y esortogonal al vectora , b

4. 𝐴 = (1, −2,−1)
𝐵⃗ = (0,1, 3)
𝑘 = 2
𝐴 + 𝐵⃗ = ( 𝑥1 + 𝑥2,𝑦1 + 𝑦2, 𝑧1 + 𝑧2)
= (1 + 0,−2 + 1,−1 + 3)
= (1, −1,2)
𝐴 + 𝐵⃗ = ( 𝑥1 − 𝑥2,𝑦1 − 𝑦2, 𝑧1 − 𝑧2)
= (1 − 0,−2 − 1,−1 − 3)
= (1,−3, −4)
K𝐴 = 2(1, −2,−1)
= (2,−4, −2)
Distanciaentre dospuntos
𝑑 = ( 𝐴,𝐵⃗ ) = √( 𝑥2 − 𝑥1)2 + ( 𝑦2 − 𝑦1)2 + ( 𝑧2 − 𝑧1)2
=√(0 − 1)2 + (1 − (−2))
2
+ (3 − (−1))
2
√1 + 9 + 16 = √26
‖ 𝑎‖ = √12 + (−2)2 + (−1)2
= √1 + 4 + 1 = √6
‖ 𝑏‖ = √02 + (1)2 + (3)2 = √1 + 9 = √10
𝑎
‖ 𝑎‖
=
1𝑖 + (−2𝑗) − 𝑘
√6
=
1𝑖
√6
,
−2
√6
,
−𝑘
√6
𝑏⃗
‖ 𝑏⃗ ‖
=
0𝑖 + 𝑗 + 3𝑘
√10
=
0𝑖
√6
,
𝑗
√6
,
3𝑘
√6
Anguloentre 2 vectores
𝑎 + 𝑏⃗ = ‖ 𝑎‖ ‖ 𝑏⃗ ‖ ∅ = 𝐶𝑜𝑠
𝑎 ∗ 𝑏⃗
‖ 𝑎‖ ‖ 𝑏⃗ ‖
∅ = 𝑐𝑜𝑠−1
−5
√6√10
= ∅ = 𝑐𝑜𝑠−1
−5
√26
= 130°

5. Ortogonalidad
𝑛⃗ = (−5,−3,1)
𝑎 ∗ 𝑛⃗ = 0
𝑎1 𝑛1 + 𝑎2 𝑛2 + 𝑎3 𝑛3
(1)(−5) + (−2)(−3) + (−1)(1)
= −5 + 6 − 1 = 0
𝑏⃗ ∗ 𝑛⃗ = 0
𝑏1 𝑛1 + 𝑏2 𝑛2 + 𝑏3 𝑛3
(0)(−5) + (1)(−3) + (3)(1)
−3 + 3 = 0