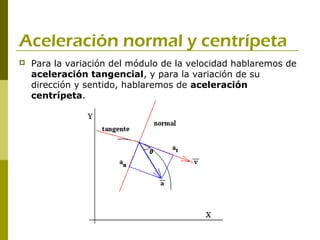
Este documento describe conceptos básicos de cinemática como velocidad, velocidad media, velocidad instantánea, aceleración, aceleración media e instantánea. Explica cómo calcular estas cantidades y la diferencia entre velocidad y aceleración tangencial frente a centrípeta. También incluye ejemplos numéricos para ilustrar los cálculos.

1. CINEMÁTICA
VELOCIDAD Y ACELERACIÓN

2. La velocidad
¿Cómo medimos la variación de posición de un
cuerpo a lo largo del tiempo?  VELOCIDAD
VELOCIDAD VELOCIDAD
MEDIA INSTANTÁNEA

3. Velocidad Media
Desplazamiento que
experimenta un punto móvil 
en la unidad de tiempo.  ∆r
v=
∆t
 
 r −r
v= Q P
t −t
Q P

4. Ejemplo 1 (actividad 11 pag. 206)
Un cuerpo se mueve según esta ecuación de
posición:  

r = 5i + (3t − 1) j
2
a)¿Qué desplazamiento ha realizado en los 10
primeros segundos?,¿En qué dirección se mueve?
b)Calcula cuál ha sido su velocidad media en ese
intervalo de tiempo.

5. Ejemplo 2
Una partícula se mueve a lo largo del eje x,
siguiendo la siguiente ecuación de su
desplazamiento:
x =t +2 2
Calcula su velocidad media.

6. Velocidad Instantánea
 La velocidad media no siempre nos sirve para definir un
movimiento.
 En ocasiones queremos conocer la velocidad de un cuerpo en un
determinado instante.
 
  ∆r  dr
 v = lim v = lim  v=
∆t dt
∆t →0 m ∆t →0
Cómo calculamos la velocidad instantánea

7. Velocidad Instantánea
Página 207 libro.
Calculamos la velocidad instantánea para t=2
segundos de un cuerpo que se mueve conforme a
la siguiente ecuación.
x = 3t − 4t m
2

8. ¿Cómo es el vector de la
Velocidad Instantánea?
El vector de la velocidad instantánea tiene la dirección
de la tangente a la trayectoria en cualquier punto, y
sentido del movimiento.

9. La aceleración
Y si la velocidad no es constante a lo largo del
movimiento. ¿Cómo medimos la variación de la
velocidad en un determinado tiempo?  ACELERACIÓN
ACELERACIÓN ACELERACIÓN
MEDIA INSTANTÁNEA

10. Aceleración Media
 De igual manera que para la velocidad media,
diremos que la aceleración media es, lo que
varia la velocidad de un cuerpo en un tiempo
determinado.
  
 ∆v v − v
a = = t 0
∆t t − t
m
t 0
 Su unidad en el sistema internacional m/s2.

11. Aceleración instantánea
 Al igual que con la velocidad, si hacemos que ∆t
tienda a “0” tendremos la aceleración
instantánea:
 
  ∆v  dv
a = lim a = lim a=
∆t dt
∆t →0 m ∆t →0

12. Aceleración normal y centrípeta
 Cuando un cuerpo se mueve describiendo una curva,
aunque su velocidad sea constante en módulo, al
variar su dirección y sentido, aparece una aceleración.

13. Aceleración normal y centrípeta
 Para la variación del módulo de la velocidad hablaremos de
aceleración tangencial, y para la variación de su
dirección y sentido, hablaremos de aceleración
centrípeta.

14. Aceleración tangencial
 Produce cambios en el módulo de la velocidad.
 Su módulo equivale a la rapidez con que cambia el modulo de la
velocidad.
dv
a =
dt
t
 Su dirección tangente a la trayectoria en todo punto.
 Su sentido en la dirección del movimiento si el modulo de la
velocidad aumenta o contrario al movimiento si el modulo de la
velocidad disminuye.
 dv 
a = u
dt
t t

15. Aceleración Centrípeta
 Aparece en movimientos curvos y sólo genera cambios en la
dirección de la velocidad, no en su módulo.
Su módulo equivale a:
v
 2
a =
r
c
 Su dirección es radial, coincide con el radio de la curva.
 Su sentido es hacia el centro de la curva.
 v  2
a = u
r
c r