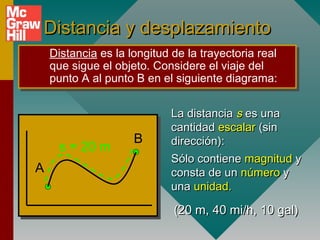
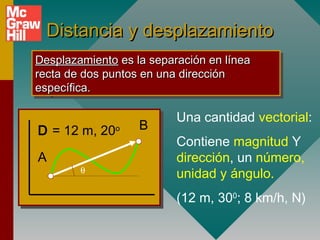
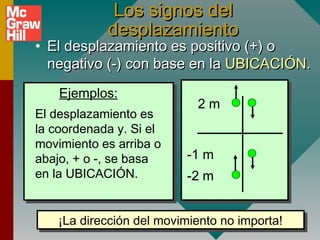
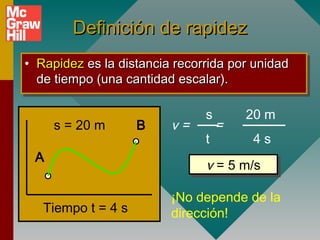
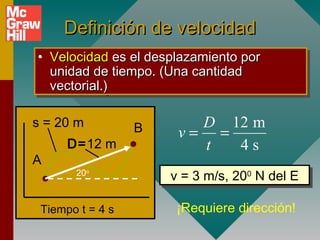
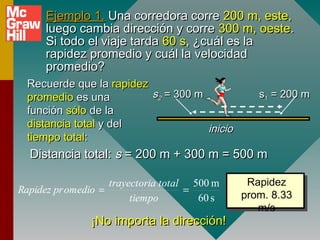
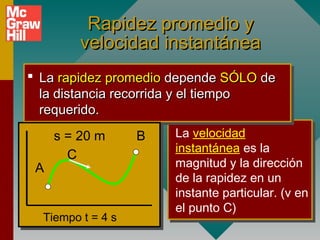
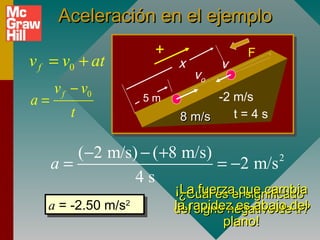
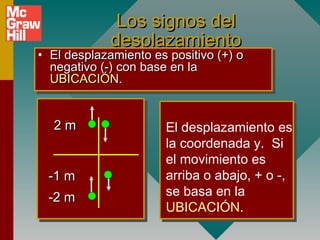
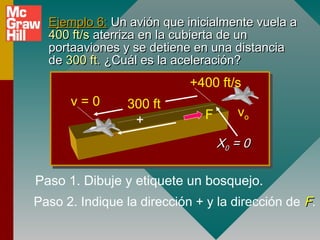
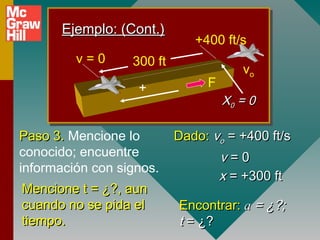
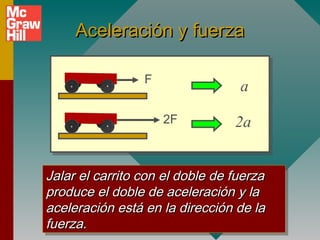
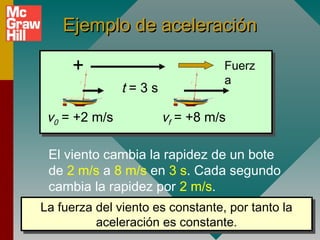
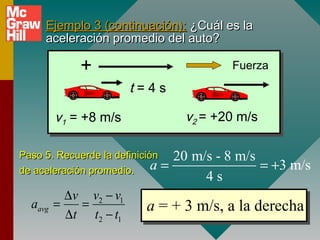
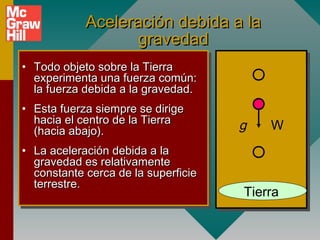
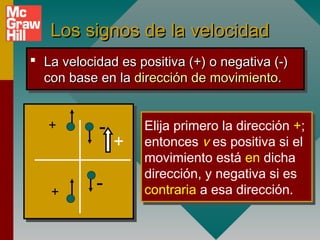
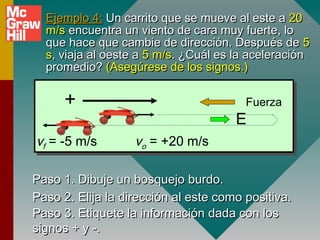
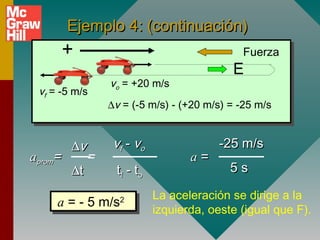
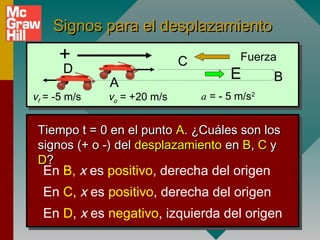
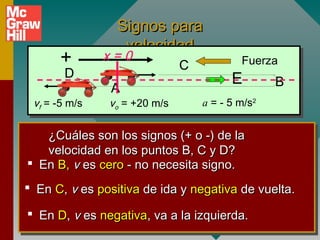
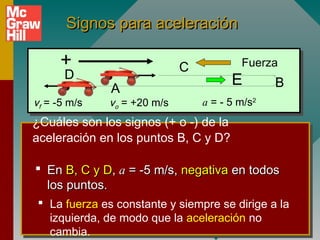
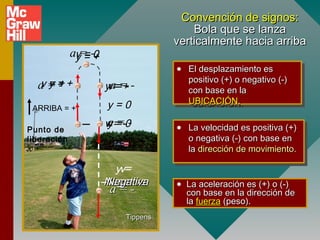
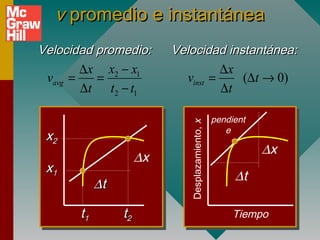
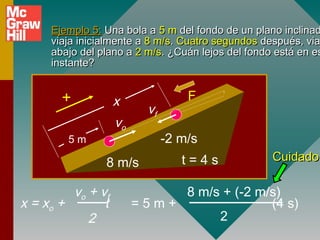
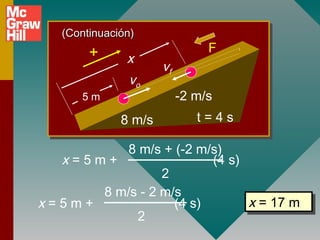
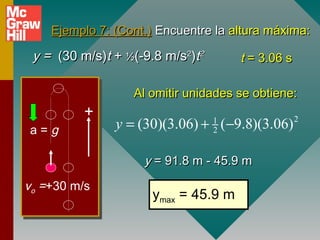
Este documento presenta conceptos fundamentales sobre aceleración, incluyendo: 1) La definición de aceleración como el cambio en la velocidad por unidad de tiempo y que depende de la fuerza aplicada. 2) Los signos de la aceleración se determinan por la dirección de la fuerza aplicada, no por la dirección del movimiento. 3) La diferencia entre aceleración promedio e instantánea y cómo se calculan.

1. Aceleración
Presentación PowerPoint de
Paul E. Tippens, Profesor de Física
Southern Polytechnic State University

2. El cheetah (guepardo): Un gato diseñado para correr. Su fortaleza
y agilidad le permiten sostener una rapidez tope de más de 100
km/h. Tales rapideces sólo se pueden mantener durante unos diez
segundos. Foto © Vol. 44 Photo Disk/Getty

3. Objetivos: Después de completar
este módulo, deberá:
• Definir y aplicar los conceptos de velocidad
promedio e instantánea y aceleración.
• Resolver problemas que involucren velocidad
inicial y final, aceleración, desplazamiento y
tiempo.
• Demostrar su comprensión de las direcciones y
signos para velocidad, desplazamiento y
aceleración.
• Resolver problemas que involucren un cuerpo en
caída libre en un campo gravitacional.

4. Aceleración uniforme en una
dirección:
• El movimiento es a lo largo de una línea recta
(horizontal, vertical o inclinado).
• Los cambios en el movimiento resultan de
una fuerza CONSTANTE que produce
aceleración uniforme.
• La causa del movimiento se discutirá más
tarde. Aquí sólo se tratan los cambios.
• El objeto en movimiento se trata como si
fuese una partícula puntual.

5. Distancia y desplazamiento
Distancia es la longitud de la trayectoria real
Distancia es la longitud de la trayectoria real
que sigue el objeto. Considere el viaje del
que sigue el objeto. Considere el viaje del
punto A al punto B en el siguiente diagrama:
punto A al punto B en el siguiente diagrama:
La distancia s es una
cantidad escalar (sin
B dirección):
s = 20 m
Sólo contiene magnitud y
A consta de un número y
una unidad.
(20 m, 40 mi/h, 10 gal)

6. Distancia y desplazamiento
Desplazamiento es la separación en línea
Desplazamiento es la separación en línea
recta de dos puntos en una dirección
recta de dos puntos en una dirección
específica.
específica.
Una cantidad vectorial:
D = 12 m, 20o B
Contiene magnitud Y
A dirección, un número,
θ
unidad y ángulo.
(12 m, 300; 8 km/h, N)

7. Distancia y desplazamiento
•• Para movimiento a lo largo de los ejes x o y,, el
Para movimiento a lo largo de los ejes x o y el
desplazamiento se determina por la coordenada x o y
desplazamiento se determina por la coordenada x o y
de su posición final. Ejemplo: Considere un auto que
de su posición final. Ejemplo: Considere un auto que
viaja 8 m al E, luego 12 m al O.
viaja 8 m al E, luego 12 m al O.
El desplazamiento neto
D es desde el origen D 8 m,E
hasta la posición final: x
D = 4 m, W
D = 4 m, W
x = -4 x = +8
¿Cuál es la distancia 12 m,O
recorrida? 20 m !!

8. Los signos del
desplazamiento
• El desplazamiento es positivo (+) o
negativo (-) con base en la UBICACIÓN.
Ejemplos:
2m
El desplazamiento es
la coordenada y. Si el
movimiento es arriba o
abajo, + o -, se basa -1 m
en la UBICACIÓN. -2 m
¡La dirección del movimiento no importa!
¡La dirección del movimiento no importa!

9. Definición de rapidez
•• Rapidez es la distancia recorrida por unidad
Rapidez es la distancia recorrida por unidad
de tiempo (una cantidad escalar).
de tiempo (una cantidad escalar).
s 20 m
s = 20 m B v= =
t 4s
A
v = 5 m/s
v = 5 m/s
¡No depende de la
Tiempo t = 4 s dirección!

10. Definición de velocidad
•• Velocidad es el desplazamiento por
Velocidad es el desplazamiento por
unidad de tiempo. (Una cantidad
unidad de tiempo. (Una cantidad
vectorial.)
vectorial.)
s = 20 m B D 12 m
v= =
D=12 m t 4s
A
20o v = 3 m/s, 2000 N del E
v = 3 m/s, 20 N del E
Tiempo t = 4 s ¡Requiere dirección!

11. Ejemplo 1. Una corredora corre 200 m, este,
luego cambia dirección y corre 300 m, oeste.
Si todo el viaje tarda 60 s, ¿cuál es la
rapidez promedio y cuál la velocidad
promedio?
Recuerde que la rapidez
promedio es una s2 = 300 m s1 = 200 m
función sólo de la
distancia total y del inicio
tiempo total:
Distancia total: s = 200 m + 300 m = 500 m
trayectoria total 500 m Rapidez
Rapidez pr omedio = =
tiempo 60 s prom. 8.33
m/s
¡No importa la dirección!

12. Ejemplo 1 (Cont.) Ahora encuentre la
velocidad promedio, que es el desplazamiento
neto dividido por el tiempo. En este caso,
importa la dirección.
t = 60 s
x f − x0 xf = -100 m x1= +200 m
v=
t
x0 = 0 m; xf = -100 m xo = 0
La dirección del
−100 m − 0 desplazamiento final es
v= = −1.67 m/s hacia la izquierda, como se
60 s muestra.
Velocidad promedio: v = 1.67 m/s, West
Nota: La velocidad promedio se dirige al oeste.

13. Ejemplo 2. Un paracaidista salta y cae 600
m en 14 s. Después se abre el paracaídas y
cae otros 400 m en 150 s. ¿Cuál es la
rapidez promedio de toda la caída?
Distancia total/tiempo total: 14 s
x A + xB 600 m + 400 m A
v= = 625 m
t A + tB 14 s + 150 s
1000 m
v= v = 6.10 m/s
164 s
B
La rapidez promedio sólo es
La rapidez promedio sólo es 356 m
función de la distancia total
función de la distancia total
recorrida y el tiempo total
recorrida y el tiempo total 142 s
requerido.
requerido.

14. Ejemplos de rapidez
Órbita
2 x 104 m/s
Luz = 3 x 108 m/s
Jets = 300 m/s Automóvil = 25 m/s

15. Ejemplos de rapidez (Cont.)
Corredora = 10 m/s
Glaciar = 1 x 10-5 m/s
Caracol = 0.001 m/s

16. Rapidez promedio y
velocidad instantánea
 La rapidez promedio depende SÓLO de
 La rapidez promedio depende SÓLO de
la distancia recorrida y el tiempo
la distancia recorrida y el tiempo
requerido.
requerido.
s = 20 m B La velocidad
La velocidad
instantánea es la
instantánea es la
C
A magnitud y la dirección
magnitud y la dirección
de la rapidez en un
de la rapidez en un
instante particular. (v en
instante particular. (v en
el punto C)
el punto C)
Tiempo t = 4 s

17. Los signos de la velocidad
 La velocidad es positiva (+) o negativa (-)
 La velocidad es positiva (+) o negativa (-)
con base en la dirección de movimiento.
con base en la dirección de movimiento.
+ - Elija primero la dirección +;
Elija primero la dirección +;
+ entonces v es positiva si el
entonces v es positiva si el
movimiento está en dicha
movimiento está en dicha
dirección, y negativa si es
dirección, y negativa si es
+
- contraria a esa dirección.
contraria a esa dirección.

18. v promedio e instantánea
Velocidad promedio: Velocidad instantánea:
∆x x2 − x1 ∆x
vavg = = vinst = (∆t → 0)
∆t t2 − t1 ∆t
pendient
Desplazamiento, x
e
x2
∆x
∆x
x1
∆t
∆t
t1 t2 Tiempo

19. Definición de aceleración
 Una aceleración es el cambio en velocidad
por unidad de tiempo. (Una cantidad
vectorial.)
 Un cambio en velocidad requiere la
aplicación de un empuje o jalón (fuerza).
Más adelante se dará un tratamiento formal de
fuerza y aceleración. Por ahora, debe saber que:
• La dirección de la • La aceleración es
aceleración es la misma proporcional a la
que la dirección de la
magnitud de la fuerza.
fuerza.

20. Aceleración y fuerza
F
a
2F 2a
Jalar el carrito con el doble de fuerza
Jalar el carrito con el doble de fuerza
produce el doble de aceleración y la
produce el doble de aceleración y la
aceleración está en la dirección de la
aceleración está en la dirección de la
fuerza.
fuerza.

21. Ejemplo de aceleración
+ Fuerz
a
t=3s
v0 = +2 m/s vf = +8 m/s
El viento cambia la rapidez de un bote
de 2 m/s a 8 m/s en 3 s. Cada segundo
cambia la rapidez por 2 m/s.
La fuerza del viento es constante, por tanto la
La fuerza del viento es constante, por tanto la
aceleración es constante.
aceleración es constante.

22. Los signos de la aceleración
•• La aceleración es positiva ((+)) o negativa ((-)
La aceleración es positiva + o negativa -)
con base en la dirección de la fuerza..
con base en la dirección de la fuerza
+ Primero elija la dirección
Primero elija la dirección
F a (-) +. Entonces la
+. Entonces la
aceleración a tendrá el
aceleración a tendrá el
mismo signo que el de la
mismo signo que el de la
a(+) fuerza F,, sin importar la
fuerza F sin importar la
F dirección de la
dirección de la
velocidad.
velocidad.

23. a promedio e instantánea
∆v v2 − v1 ∆v
aavg = = ainst = (∆t → 0)
∆t t2 − t1 ∆t
pendiente
v2
∆v
∆v
v1
∆t
∆t
t1 t2 tiempo

24. Ejemplo 3 (sin cambio en dirección): Una fuerza
constante cambia la rapidez de un auto de 8 m/s a
20 m/s en 4 s. ¿Cuál es la aceleración promedio?
+ Fuerza
t=4s
v1 = +8 m/s v2 = +20 m/s
Paso 1. Dibuje un bosquejo burdo.
Paso 2. Elija una dirección positiva (derecha).
Paso 3. Etiquete la información dada con signos + y -.
Paso 4. Indique la dirección de la fuerza F.

25. Ejemplo 3 (continuación): ¿Cuál es la
aceleración promedio del auto?
+ Fuerza
t=4s
v1 = +8 m/s v2 = +20 m/s
Paso 5. Recuerde la definición 20 m/s - 8 m/s
de aceleración promedio. a= = +3 m/s
4s
∆v v2 − v1
aavg = = a = + 3 m/s, a la derecha
∆t t2 − t1

26. Ejemplo 4: Un carrito que se mueve al este a 20
m/s encuentra un viento de cara muy fuerte, lo
que hace que cambie de dirección. Después de 5
s, viaja al oeste a 5 m/s. ¿Cuál es la aceleración
promedio? (Asegúrese de los signos.)
+ Fuerza
E
vf = -5 m/s vo = +20 m/s
Paso 1. Dibuje un bosquejo burdo.
Paso 2. Elija la dirección al este como positiva.
Paso 3. Etiquete la información dada con los
signos + y -.

27. Ejemplo 4 (Cont.): El carrito que se mueve al este
a 20 m/s encuentra un viento de cara que hace
que cambie de dirección. Cinco segundos
después, viaja al oeste a 5 m/s. ¿Cuál es la
aceleración promedio?
Elija la dirección al este como positiva.
Elija la dirección al este como positiva.
Velocidad inicial, voo = +20 m/s, este (+)
Velocidad inicial, v = +20 m/s, este (+)
Velocidad final, vf f = -5 m/s, oeste (-)
Velocidad final, v = -5 m/s, oeste (-)
Cambio en velocidad, ∆v = vf f -- v00
Cambio en velocidad, ∆v = v v
∆v = (-5 m/s) -- (+20 m/s) = -25 m/s
∆v = (-5 m/s) (+20 m/s) = -25 m/s

28. Ejemplo 4: (continuación)
+ Fuerza
E
vo = +20 m/s
vf = -5 m/s
∆v = (-5 m/s) - (+20 m/s) = -25 m/s
∆v vf - vo -25 m/s
aprom= = a=
∆t tf - to 5s
La aceleración se dirige a la
a = -- 5 m/s
a = 5 m/s 22
izquierda, oeste (igual que F).

29. Signos para el desplazamiento
+ C Fuerza
D E
A B
vf = -5 m/s vo = +20 m/s a = - 5 m/s2
Tiempo t = 0 en el punto A. ¿Cuáles son los
signos (+ o -) del desplazamiento en B, C y
D?
En B, x es positivo, derecha del origen
En C, x es positivo, derecha del origen
En D, x es negativo, izquierda del origen

30. Signos para
velocidad
+ x=0
C Fuerza
D E
A B
vf = -5 m/s vo = +20 m/s a = - 5 m/s2
¿Cuáles son los signos (+ o -) de la
velocidad en los puntos B, C y D?
 En B, v es cero - no necesita signo.
 En C, v es positiva de ida y negativa de vuelta.
 En D, v es negativa, va a la izquierda.

31. Signos para aceleración
+ C Fuerza
D E
A B
vf = -5 m/s vo = +20 m/s a = - 5 m/s2
¿Cuáles son los signos (+ o -) de la
aceleración en los puntos B, C y D?
 En B, C y D, a = -5 m/s, negativa en todos
los puntos.
 La fuerza es constante y siempre se dirige a la
izquierda, de modo que la aceleración no
cambia.

32. Definiciones
Velocidad promedio:
∆x x2 − x1
vavg = =
∆t t2 − t1
Aceleración promedio:
∆v v2 − v1
aavg = =
∆t t2 − t1

33. Velocidad para a constante
Velocidad promedio: Velocidad promedio:
=
∆x x f − x0
=
v0 + v f
vavg
∆ t t f − t0 vavg =
2
Al hacer to = 0 y combinar lo que se tiene:
v0 + v f
x = x0 + t
2

34. Ejemplo 5: Una bola a 5 m del fondo de un plano inclinad
viaja inicialmente a 8 m/s. Cuatro segundos después, via
abajo del plano a 2 m/s. ¿Cuán lejos del fondo está en es
instante?
+ x F
vf
vo
5m -2 m/s
8 m/s t=4s Cuidado
vo + vf 8 m/s + (-2 m/s)
x = xo + t =5m+ (4 s)
2 2

35. (Continuación)
+ F
x
vf
vo
5m -2 m/s
8 m/s t=4s
8 m/s + (-2 m/s)
x=5m+ (4 s)
2
8 m/s - 2 m/s
x=5m+ (4 s) x = 17 m
x = 17 m
2

36. Aceleración constante
∆v v f − v0
Aceleración: a avg = =
∆t t f − t0
Al hacer to = 0 y resolver para v, se tiene:
v f = v0 + at
Velocidad final = velocidad inicial + cambio en velocidad

37. Aceleración en el ejemplo
+ F
v f = v0 + at x v
vo
v f − v0
a= 5m -2 m/s
t 8 m/s t=4s
(−2 m/s) − ( +8 m/s)
a= = −2 m/s 2
4s
¡La fuerza que cambia
¿Cuál es el significado
a = -2.50 m/s22
a = -2.50 m/s delrapidez es abajo del
la signo negativo de a?
plano!

38. Fórmulas basadas en definicione
v0 + v f
x = x0 + t v f = v0 + at
2
Fórmulas derivadas:
derivadas
x = x0 + v0t + at 1
2
2
x = x0 + v f t − at
1
2
2
2a ( x − x0 ) = v − v
2
f
2
0
Sólo para aceleración constante

39. Uso de posición inicial x0 en
problemas.
0 v0 + v f Si elige el origen de
Si elige el origen de
x = x0 + t sus ejes x,y en el
sus ejes x,y en el
2 punto de la posición
punto de la posición
0 inicial, puede hacer
inicial, puede hacer
x = x0 + v0t + at 1 2
x00 = 0 y simplificar
2 x = 0 y simplificar
0 estas ecuaciones.
estas ecuaciones.
x = x0 + v f t − at 1
2
2
0 El término xo es muy
2a ( x − x0 ) = v − v 2
f
2
0 útil para estudiar
problemas que
v f = v0 + at involucran movimiento
de dos cuerpos.

40. Repaso de símbolos y unidades
•• Desplazamiento ((x, xo); metros ((m))
Desplazamiento x, xo); metros m
•• Velocidad ((v, vo); metros por segundo ((m/s))
Velocidad v, vo); metros por segundo m/s
•• Aceleración ((a); metros por s22 ((m/s2))
Aceleración a ); metros por s m/s2
•• Tiempo ((tt); segundos ((s))
Tiempo ); segundos s
Repase la convención de signos para cada
símbolo

41. Los signos del
desplazamiento
•• El desplazamiento es positivo (+) o
El desplazamiento es positivo (+) o
negativo (-) con base en la
negativo (-) con base en la
UBICACIÓN..
UBICACIÓN
2m El desplazamiento es
la coordenada y. Si
el movimiento es
-1 m arriba o abajo, + o -,
-2 m se basa en la
UBICACIÓN.

42. Los signos de la velocidad
•• La velocidad es positiva (+) o negativa (-)
La velocidad es positiva (+) o negativa (-)
con base en la dirección de movimiento..
con base en la dirección de movimiento
+
+ - Elija primero la dirección +;
entonces la velocidad v es
positiva si el movimiento
está en la dirección +, y
+
- negativa si está contraria a
esa dirección.

43. Aceleración producida por una fuerz
•• La aceleración es ((+)) o ((-) con base en la
La aceleración es + o -) con base en la
dirección de la fuerza ((NO con base en v).
dirección de la fuerza NO con base en v).
Se necesita un empujón o
jalón (fuerza) para cambiar la
F a(-) velocidad, por tanto el signo
de a es igual al signo de F.
F a(+) Después se hablará
más de la relación
entre F y a.

44. Estrategia para resolución de problemas
problema
 Dibuje y etiquete bosquejo del problema.
 Indique la dirección + y la dirección de la fuerza.
 Mencione la información dada y establezca lo que
se tiene que encontrar.
Dada: ____, _____, _____ (x,v,vo,a,t)
Encontrar: ____, _____
 Seleccione la ecuación que contenga una
y no las otras cantidades desconocidas y
resuelva para la incógnita.

45. Ejemplo 6: Un avión que inicialmente vuela a
400 ft/s aterriza en la cubierta de un
portaaviones y se detiene en una distancia
de 300 ft. ¿Cuál es la aceleración?
+400 ft/s
v=0 300 ft
F vo
+
X0 = 0
Paso 1. Dibuje y etiquete un bosquejo.
Paso 2. Indique la dirección + y la dirección de F.

46. Ejemplo: (Cont.)
+400 ft/s
v=0 300 ft
vo
+ F
X0 = 0
Paso 3. Mencione lo Dado: vo = +400 ft/s
conocido; encuentre v=0
información con signos.
x = +300 ft
Mencione t = ¿?, aun
cuando no se pida el Encontrar: a = ¿?;
tiempo. t = ¿?

47. Continúa . . . x +400 ft/s
v=0 300 ft
vo
+ F
X0 = 0
Paso 4. Seleccione la
0 0
ecuación que contiene a y no 2a(x -xo) = v2 - vo2
t.
-vo2 La posición inicial y la
-(400 ft/s)2
a= = velocidad final son
a = -- 267 ft/s22
2x 2(300 ft) cero.= 267 ft/s
a
¿Por quéla fuerza está en una dirección
¡Porque la aceleración es negativa?
negativa!

48. Aceleración debida a la
gravedad
•• Todo objeto sobre la Tierra
Todo objeto sobre la Tierra
experimenta una fuerza común:
experimenta una fuerza común:
la fuerza debida a la gravedad.
la fuerza debida a la gravedad.
•• Esta fuerza siempre se dirige
Esta fuerza siempre se dirige
hacia el centro de la Tierra
hacia el centro de la Tierra
(hacia abajo). g W
(hacia abajo).
•• La aceleración debida a la
La aceleración debida a la
gravedad es relativamente
gravedad es relativamente
constante cerca de la superficie
constante cerca de la superficie
terrestre.
terrestre.
Tierra

49. Aceleración gravitacional
•• En un vacío, todos los objetos
En un vacío, todos los objetos
caen con la misma aceleración.
caen con la misma aceleración.
•• Las ecuaciones para
Las ecuaciones para
aceleración constante se aplican
aceleración constante se aplican
como es usual.
como es usual.
•• Cerca de la superficie de la
Cerca de la superficie de la
Tierra:
Tierra:
a = g = 9.80 m/s2 o 32 ft/s2
Dirigida hacia abajo (por lo general negativa).

50. Determinación experimental
de la aceleración
gravitacional. ∆t
El aparato consiste de un
dispositivo que mide el tiempo
que una bola requiere para caer
una distancia dada. y
Suponga que la altura es 1.20
m y que el tiempo de caída
registrado es 0.650 s. ¿Cuál
es la aceleración debida a la
gravedad?

51. Determinación experimental de la
gravedad (y0 = 0; y = -1.20 m)
y = -1.20 m; t = 0.495 s ∆t
y = v0t + 1 at 2 ; v0 = 0
2
2 y 2(−1.20 m)
a= 2 =
y
2
t (0.495 s) +
Aceleración de
la gravedad: a = −9.79 m/s 2
W
La aceleración a es negativa
porque la fuerza W es negativa.

52. Convención de signos:
Bola que se lanza
verticalmente hacia arriba
av= -0
y=+
=
•• El desplazamiento es
El desplazamiento es
positivo (+) o negativo (-)
a == +
vy +
=- ya= + -
v ==- positivo (+) o negativo (-)
con base en la
con base en la
UBICACIÓN..
ARRIBA = + y=0 UBICACIÓN
a= -
y=
v = -0
Punto de •• La velocidad es positiva (+)
La velocidad es positiva (+)
liberación o negativa (-) con base en
o negativa (-) con base en
la dirección de movimiento..
la dirección de movimiento
yv=
=
--Negativa
Negativa • La aceleración es (+) o (-)
a=- con base en la dirección de
la fuerza (peso).
Tippens

53. Misma estrategia de
resolución de problemas,
excepto a = g:
 Dibuje y etiquete bosquejo del problema.
 Indique la dirección + y la dirección de la fuerza.
 Mencione la información dada y establezca la que
se tiene que encontrar.
Dado: ____, _____, a = - 9.8 m/s2
Encontrar: ____, _____
 Seleccione la ecuación que contenga una
y no las otras cantidades desconocidas, y
resuelva para la incógnita.

54. Ejemplo 7: Una bola se lanza verticalmente haci
arriba con una velocidad inicial de 30 m/s.
¿Cuáles son su posición y velocidad después de
2 s, 4 s y 7 s ?
Paso 1. Dibuje y etiquete un
bosquejo.
Paso 2. Indique la dirección +
+
y la dirección de la fuerza. a=g
Paso 3. Información
dada/encontrar.
a = -9.8 ft/s2 t = 2, 4, 7 s
vo = +30 m/s
vo = + 30 m/s y = ¿? v = ¿?

55. Encontrar desplazamiento:
Paso 4. Seleccione ecuación
que contenga y y no v. +
0 a=g
y = y0 + v0t + at
1
2
2
y = (30 m/s)t + ½(-9.8 m/s2)t2
La sustitución de t = 2, 4 y 7 s vo = 30 m/s
dará los siguientes valores:
y = 40.4 m; y = 41.6 m; y = -30.1 m
y = 40.4 m; y = 41.6 m; y = -30.1 m

56. Encontrar velocidad:
Paso 5. Encuentre v a partir de la
Paso 5. Encuentre v a partir de la
ecuación que contenga v y no x::
ecuación que contenga v y no x
+
a=g
v f = v0 + at
v f = 30 m/s + (−9.8 m/s )t 2
vo = 30 m/s
Sustituya t = 2, 4 y 7 s:
v = +10.4 m/s; v = -9.20 m/s; v = -38.6 m/s
v = +10.4 m/s; v = -9.20 m/s; v = -38.6 m/s

57. Ejemplo 7: (Cont.) Ahora
encuentre la altura máxima
alcanzada:
El desplazamiento es máximo +
cuando la velocidad vf es cero.
a=g
v f = 30 m/s + (−9.8 m/s )t = 0
2
30 m/s
t= 2
; t = 3.06 s
9.8 m/s
Para encontrar ymax sustituya
vo = +96 ft/s
t = 3.06 s en la ecuación
general del desplazamiento.
y = (30 m/s)t + ½(-9.8 m/s2)t2

58. Ejemplo 7: (Cont.) Encuentre la altura máxima:
y = (30 m/s)t + ½(-9.8 m/s2)t2 t = 3.06 s
Al omitir unidades se obtiene:
+
a=g y = (30)(3.06) + ( −9.8)(3.06)
1
2
2
y = 91.8 m - 45.9 m
vo =+30 m/s
ymax = 45.9 m

59. Resumen de fórmulas
v0 + v f
x = x0 + t v f = v0 + at
2
Fórmulas derivadas:
derivadas
x = x0 + v0t + at 1
2
2
x = x0 + v f t − at
1
2
2
2a ( x − x0 ) = v − v
2
f
2
0
Sólo para aceleración constante

60. Resumen: Procedimiento
 Dibuje y etiquete bosquejo del problema.
 Indique la dirección + y la dirección de la fuerza.
 Mencione la información dada y establezca la que
debe encontrar.
Dada: ____, _____, ______
Encontrar: ____, _____
 Seleccione la ecuación que contenga una y no
la otra de las cantidades desconocidas, y
resuelva para la incógnita.

61. CONCLUSIÓN:
Aceleración