5. medidas descriptivas (datos agrupados)
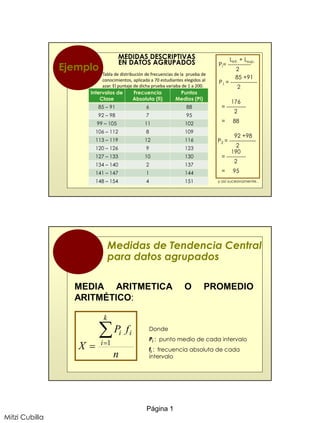
- 1. Página 1 Mitzi Cubilla Ejemplo Linf. + Lsup. Pi= ------------ 2 85 +91 P1 = -------------- 2 176 = ---------- 2 = 88 MEDIDAS DESCRIPTIVAS EN DATOS AGRUPADOS 92 +98 P2 = -------------- 2 190 = ---------- 2 = 95 y así sucesivamente.. Intervalos de Clase Frecuencia Absoluta (fi) Puntos Medios (Pi) 85 – 91 6 88 92 – 98 7 95 99 – 105 11 102 106 – 112 8 109 113 – 119 12 116 120 – 126 9 123 127 – 133 10 130 134 – 140 2 137 141 – 147 1 144 148 – 154 4 151 Tabla de distribución de frecuencias de la prueba de conocimientos, aplicada a 70 estudiantes elegidos al azar. El puntaje de dicha prueba variaba de 1 a 200. Medidas de Tendencia Central para datos agrupados MEDIA ARITMETICA O PROMEDIO ARITMÉTICO: n fP X k i ii 1 Donde Pi : punto medio de cada intervalo fi : frecuencia absoluta de cada intervalo
- 2. Página 2 Mitzi Cubilla Ejemplo 10.151./ 50 75551 B n fP X k i ii suma = 7480 El puntaje promedio de la prueba de conocimientos fue de: 106.9 puntos Intervalos de Clase Frecuencia Absoluta (fi) Puntos Medios (Pi) Pi x fi 85 – 91 6 88 528 92 – 98 7 95 665 99 – 105 11 102 1122 106 – 112 8 109 872 113 – 119 12 116 1392 120 – 126 9 123 1107 127 – 133 10 130 1300 134 – 140 2 137 274 141 – 147 1 144 144 148 – 154 4 151 604 7480 70 106.9 puntos MEDIANA: ES EL VALOR QUE DIVIDE A LA POBLACION EN DOS PARTES IGUALES. SE REPRESENTA POR Me. Medidas de Tendencia Central para datos agrupados m am ri f AF n LMe 2 Donde: Lri : límite real inferior que contiene a la mediana Fam: frecuencia absoluta acumulada del intervalo que antecede al intervalo mediano. A: amplitud del intervalo mediano fm: frecuencia absoluta del intervalo que contiene a la mediana
- 3. Página 3 Mitzi Cubilla Pasos para calcular la Mediana 1. En la tabla de distribución de frecuencias se determina la columna de las “frecuencias absolutas acumuladas” (Fi) 2. Se calcula n/2 (número total de datos entre dos) 3. En la columna de las Fi se ubica la fila que corresponde al valor n/2 4. En caso de que n/2 no coincida exactamente con algún Fi, entonces debemos ubicar un Fi que se encuentre en la fila inmediata superior a n/2 con lo cual determinamos el intervalo mediano teórico. Ejemplo m am ri f AF n LMe 2 La mitad de los estudiantes obtienen un puntaje de ________ o más Intervalos de Clase Límite Real Frecuencia Absoluta (fi) Frecuencia absoluta acumulada 85 – 91 84.5 – 91.5 6 6 92 – 98 91.5 – 98.5 7 13 99 – 105 98.5 – 105.5 11 24 106 – 112 105.5 – 112.5 8 32 113 – 119 112.5 – 119.5 12 44 120 – 126 119.5 – 126.5 9 53 127 – 133 126.5 – 133.5 10 63 134 – 140 133.5 – 140.5 2 65 141 – 147 140.5 – 147.5 1 66 148 – 154 147.5 – 154.5 4 70 114.25 Intervalo mediano 114.25
- 4. Página 4 Mitzi Cubilla MODA: ES EL VALOR DE LA VARIABLE QUE MAS VECES SE REPITE. SE DENOTA COMO Mo. Medidas de Tendencia Central para datos agrupados A RR R LMo i 21 1 Donde Li : límite inferior del intervalo modal R1: diferencia entre la frecuencia absoluta del intervalo modal y el intervalo inmediatamente anterior. R2: diferencia entre la frecuencia absoluta del intervalo modal y el intervalo siguiente. A: amplitud del intervalo modal Ejemplo A RR R LMo i 21 1 Intervalos de Clase Límite Real Frecuencia Absoluta (fi) Frecuencia absoluta acumulada 85 – 91 84.5 – 91.5 6 6 92 – 98 91.5 – 98.5 7 13 99 – 105 98.5 – 105.5 11 24 106 – 112 105.5 – 112.5 8 32 113 – 119 112.5 – 119.5 12 44 120 – 126 119.5 – 126.5 9 53 127 – 133 126.5 – 133.5 10 63 134 – 140 133.5 – 140.5 2 65 141 – 147 140.5 – 147.5 1 66 148 – 154 147.5 – 154.5 4 70 = 116.5 Intervalo modal
- 5. Página 5 Mitzi Cubilla Ejemplo 1 1 2 12 2 n n fP fP S k i k i ii ii Desviación Estándar (s) Intervalos de Clase Frecuencia Absoluta (fi) Puntos Medios (Pi) Pi x fi 85 – 91 6 88 528 92 – 98 7 95 665 99 – 105 11 102 1122 106 – 112 8 109 872 113 – 119 12 116 1392 120 – 126 9 123 1107 127 – 133 10 130 1300 134 – 140 2 137 274 141 – 147 1 144 144 148 – 154 4 151 604 Medidas de Dispersión para datos agrupados Pi 2 x fi 46464 63175 114444 95048 Complete la última columna, reemplace en la fórmula y obtenga la desviación estándar s Medidas de Dispersión para datos agrupados Coeficiente de Variación 100*.. x S VC Resuelva para el ejemplo en cuestión