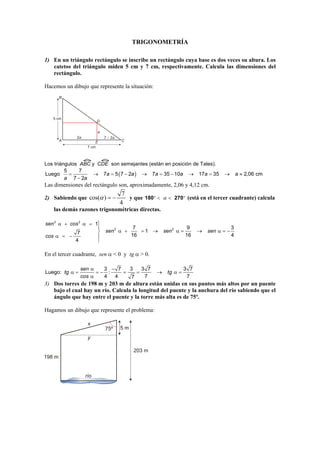
1. TRIGONOMETRÍA
1) En un triángulo rectángulo se inscribe un rectángulo cuya base es dos veces su altura. Los
catetos del triángulo miden 5 cm y 7 cm, respectivamente. Calcula las dimensiones del
rectángulo.
Hacemos un dibujo que represente la situación:
Los triángulos ABC y CDE son semejantes (están en posición de Tales).
5 7
Luego = → 7a = 5 ( 7 − 2a ) → 7a = 35 − 10a → 17a = 35 → a ≈ 2,06 cm
a 7 − 2a
Las dimensiones del rectángulo son, aproximadamente, 2,06 y 4,12 cm.
7
2) Sabiendo que cos(α ) = − y que 180° < α < 270° (está en el tercer cuadrante) calcula
4
las demás razones trigonométricas directas.
sen 2 α + cos 2 α = 1
 7 9 3
7  sen 2 α + =1 → sen 2 α = → sen α = −
cos α = −  16 16 4
4 
En el tercer cuadrante, sen α < 0 y tg α > 0.
sen α 3 − 7 3 3 7 3 7
Luego: tg α = =− : = = → tg α =
cos α 4 4 7 7 7
3) Dos torres de 198 m y 203 m de altura están unidas en sus puntos más altos por un puente
bajo el cual hay un río. Calcula la longitud del puente y la anchura del río sabiendo que el
ángulo que hay entre el puente y la torre más alta es de 75º.
Hagamos un dibujo que represente el problema:

2. Llamamos x = longitud del puente, y = anchura del río
Observamos que tenemos un triángulo rectángulo del cual conocemos el cateto contiguo al ángulo
de 75º: 203-198 =5 m.
5 5 5
cos 75° = →x= ≈ ≈ 19,23 m
x cos 75° 0,26
y
sen 75° = → y = x ⋅ sen 75° ≈ 19,23 ⋅ 0,97 ≈ 18,65 m
x
La longitud del puente es de 19,23 m, y la anchura del río, 18,65 m.
4) Halla la distancia entre los puntos P(6, -2) y Q(0, 6).
dist ( P, Q ) = (0 − 6) + ( 6 − ( −2 ) ) = 62 + 82 = 36 + 64 = 100 = 10
2 2
5) Resuelve:
a) Halla la ecuación de la recta, r, que pasa por (3, 2) y tiene como vector dirección
d (1, 1) .
b) Escribe la ecuación de la recta, s, que pasa por (5, 2) y es paralelo al eje X.
c) Obtén el punto de corte de las dos rectas anteriores.
1
a) Pendiente = =1
1
Ecuación: y = 2 + 1( x-3)  , es decir x - y-1=0
B) y = 2
C) Es la solución de este sistema:
y = x − 1
x −1= 2 → x=3 Punto: ( 3, 2 )
y =2 
6) Una piscina tiene 2,3 m de ancho; situándonos a 116 cm del borde, desde una altura de
1,74 m, observamos que la visual une el borde de la piscina con la línea del fondo. ¿Qué
profundidad tiene la piscina?
Hacemos un dibujo que refleje la situación:

3. Llamamos x a la profundidad de la piscina
Los triángulos ABC y CDE son semejantes (sus ángulos son iguales).
2,3 x 2,3 ⋅ 1,74
Luego: = → x= = 3,45 m , y por tanto la profundidad es de 3,45m.
1,16 1,74 1,16
5
7) De un ángulo agudo sabemos que tg ( α ) = , calcula su seno y coseno.
4
Una forma seria la siguiente:
5 sen α 5 5 
tg α = → = → sen α = cos α 
4 cos α 4 4  →
sen 2 α + cos 2 α = 1

2
5  25 41
→  cos α  + cos α = 1 →
2
cos 2 α + cos 2 α = 1 → cos 2 α = 1 →
4  16 16
16 4 4 41 5
→ cos 2 α = → cos α = → cos α = ≈ 0,62 sen α = ⋅ 0,62 ≈ 0,78
41 41 41 4
1
Otra forma más sencilla es utilizar que 1 + tg 2 (α ) = , con lo cual
cos (α )
2
1 1 16 5
cos (α ) = = = ≈ 0, 62 y posteriormente sen ( α ) = ⋅ 0,62 ≈ 0,78
1 + tg 2 (α ) 5
2
41 4
1+  
4
8) El lado de un rectángulo mide 4 m y la diagonal forma con dicho lado un ángulo de 33 .
Calcula la longitud de la diagonal y el área del rectángulo.
Llamamos: d a la longitud de la diagonal, y x a la longitud del otro lado
Nos dan un ángulo y el lado contiguo a este ángulo. Para calcular d y x, usamos el coseno y la
tangente, respectivamente:
4 4 4 x
cos 33° = →d = ≈ ≈ 4,76 m tg 33° = → x = 4 ⋅ tg 33° ≈ 4 ⋅ 0,65 = 2,6 m
d cos 33° 0,84 4
La longitud de la diagonal es de 4,76 m.
Calculamos el área: A = 4 · 2,6 = 10,4 . El área del rectángulo es 10,4 m2.

4. 8   1 
9) Calcula la distancia entre los puntos M  , 1 y N  − , 5  .
2   3 
2
 1 8
dist ( M, N ) =  − −  + ( 5 − 1) = 32 + 42 = 9 + 16 = 25 = 5
2
 3 3
10) Calcula
a) Recta r, que pasa por el punto (0, 0) y tiene como vector director d ( 3, 6 ) .
b) Escribe la ecuación general de la recta, s, que pasa por (3, 4) y es perpendicular a
la recta x +y - 5 =0.
c) Obtén el punto de intersección de las dos rectas anteriores.
6
a ) Pendiente = =2
3
Ecuación: y = 2 x
−1 −1
b) Pendiente de x + y-5=0, m =-1, la perpendicular tendrá pendiente = =1
m −1
Ecuación de s: y = 4+ 1 (x- 3) , es decir x –y+1=0
c) Es la solución del siguiente sistema:
y = 2x  x − 2x + 1 = 0 → x = 1 → y =2

x − y + 1 = 0 Punto: (1, 2 )
11) Dos farmacias se encuentran en un mismo edificio por la misma cara. Cristina, que está en
el portal del edificio de enfrente, quiere comprar un medicamento. Observa el dibujo e
indica cuál de las dos farmacias está más cerca de Cristina haciendo los cálculos que
correspondan. ¿A qué distancia está Cristina del quiosco?
Según el dibujo, las visuales desde donde está Cristina a las farmacias forman un ángulo de 90º.
Pongamos los datos en el triángulo:

5. Calculamos x e y aplicando el teorema del cateto:
x 2 = 18,05 ⋅ 21,25  x 2 ≈ 383,56 → x ≈ 19,58 m
 →
y 2 = 3,2 ⋅ 21,25  y 2 ≈ 68 → y ≈ 8,25 m
Cristina está más cerca de la farmacia 2.
Calculamos h usando el teorema de la altura:
h2 = 18,05 · 3,2 ; h2 = 57,76 y por tanto h = 7,6 m , Cristina está a 7,6 m del quiosco.
12) Calcula sen α y tg α de un ángulo agudo, α, sabiendo que cos (α) = 0,6.
sen2 α+ cos2 α = 1 → sen2 α + 0,62 = 1 → sen2 α = 1 − 0,36 → sen2 α = 0,64 → sen α = 0,8
sen α 0,8
Luego: tg α = = = 1,3 → tg α = 1,3
cos α 0,6
13) Una escalera de 5 m está apoyada en una pared formando un ángulo de 46 . Calcula la
distancia entre la base de la escalera y la pared. ¿Qué ángulo forma la escalera con el
suelo?
Llamamos: x → distancia entre la base de la escalera y la pared,
α → ángulo entre la escalera y el suelo
Conocemos la hipotenusa y un ángulo agudo, y nos piden calcular el cateto opuesto a ese ángulo;
usamos el seno como razón trigonométrica:
x
sen 46° = → x = 5 ⋅ sen 46° ≈ 5 ⋅ 0,72 = 3,6
5
La distancia entre la base de la escalera y la pared es de 3,6 m.
Calculamos α → 46° + 90° + α = 180° → α = 44° es la inclinación que hay entre la escalera
y el suelo.
14) Halla la distancia entre los puntos Α(−4, 12) y Β(11, −8).
dist ( A, B ) = (11 − ( −4 ) ) + ( −8 − 12)
2 2
= 152 + 202 = 225 + 400 = 625 = 25

6. 15) Calcula:
α) Escribe la ecuación general de la recta, r, que pasa por los puntos (1, 0) y (3, 6).
1
b) Halla la ecuación de la recta , s, paralela a y = x que pasa por el punto (4, 4)
2
c) Obtén el punto de corte de las dos rectas anteriores.
6−0 6
a ) Pendiente = = =3
3 −1 2
Ecuación: y = 0 + 3(x − 1) → y = 3x − 3 → 3x − y − 3 = 0
1
b ) Si son paralelas, tienen la misma pendiente: m = .
2
1
Ecuación: y = 4 + ( x − 4) → 2y = 8 + x − 4 → x − 2y + 4 = 0
2
c)Es la solución del sistema siguiente:
3x − y − 3 = 0 y = 3x − 3

x − 2y + 4 = 0  x − 2 ( 3 x − 3 ) + 4 = 0 → x − 6x + 6 + 4 = 0 → −5 x = −10 → x=2 →
→ y =3 Punto: ( 2, 3 )
16) Completa la siguiente tabla haciendo uso de las relaciones fundamentales y sabiendo que
α es un ángulo agudo:
sen α
cos α 0,25
tg α 0,6
• Si cos α = 0,25 → 0,252 + sen2 α = 1 → sen2 α = 0,9375
0,97
Luego, sen α ≈ 0,97 y tg α = ≈ 3,88.
0,25
• Si tg α = 0,6 → sen α = 0,6 cos α → (0,6 cos α)2 + cos2 α = 1
0,36 cos2 α +cos2 α = 1 → 1,36 cos2 α = 1 → cos2 α ≈ 0,74 → cos α ≈ 0,86
Luego, sen α = 0,6 · 0,86 ≈ 0,52 y la tabla queda:
sen α 0,97 0,52
cos α 0,25 0,86
tg α 3,88 0,6

7. 2
17) Si cos α = y 270° < α < 360°, calcula sen α y tg α. (esta en el 4º cuadrante)
3
En el cuarto cuadrante, sen α < 0 y tg α < 0.
2
 2 2 7
sen α + cos α = 1 →
2 2
 + sen 2 α = 1 → sen 2 α = 1 − → sen α = −
 3 
 9 3
 
sen α  7 2 7 14 14
tg α = = − : =− =− → tg α = −
cos α  3  3
  2 2 2
18) Carlos sube por una rampa de 35 m hasta el tejado de su casa. Estando ahí, mide la visual
entre su casa y la rampa, resultando ser de 70°. Calcula la altura de la casa de Carlos y el
ángulo que hay entre la rampa y el suelo.
Llamamos h a la altura de la casa y al ángulo que hay entre la rampa y el suelo.
Calculamos α: 90° + 70° + α = 180° → α = 20°
h
Calculamos h: cos 70° = → h = 35 ⋅ cos 70° ≈ 35 ⋅ 0,34
35
h = 11,9 m es la altura de la casa de Carlos.
19) La base de un triángulo isósceles mide 64 cm, y el ángulo que se forma entre los lados
iguales es de 40°. Calcula el perímetro y el área del triángulo.
Trazamos la altura sobre la base para conseguir dos triángulos rectángulos.
Para calcular el perímetro y el área, necesitamos conocer el valor de la altura, h, y del otro lado, x.
En cada triángulo conocemos el ángulo de 20° y el cateto opuesto a este ángulo que mide

8. 64
= 32 cm.
2
32 32 32
sen 20° = → x= ≈ = 94,12 cm
x sen 20° 0,34
h h
cos 20° = → cos 20° = → h = 94,12 ⋅ cos 20°
x 94,12
h ≈ 94,12 · 0,94 ≈ 88,47 cm
64 ⋅ 88,47
Luego: Perímetro = 64  2 · 94,12 = 252,24 cm, y el Área = = 2831,04 cm2
2
3
20) De un ángulo agudo conocemos que sen α = . Halla cos α y tg α.
5
2
3 9
sen 2 α + cos 2 α = 1 →   + cos 2 α = 1 → + cos 2 α = 1
5 25
9 16 4
cos 2 α = 1 − → cos 2 α = → cos α =
25 25 5
sen α 3 4 3 3
tg α = = : = → tg α =
cos α 5 5 4 4
21) Sabiendo que tg α = − 5 y α ∈ 2º cuadrante. Halla cos α y sen α.
Como tg α = − 5 → sen α = − 5 cos α
sen α + cos α = 1 →
2 2
5 cos 2 α + cos 2 α = 1 →
1 1 6
→ 6 cos 2 α = 1 → cos 2 α = → cos α = − =− ,
6 6 6
por estar α en el 2º cuadrante.
 6 30
Así, sen α = − 5  − = . 6 30
 6  6 La solución es: cos α = y sen α =
  6 6
22) Un tronco de 6,2 m está apoyado en una pared y forma con el suelo un ángulo de 55°.¿A
qué altura de la pared se encuentra apoyado? Calcula la distancia desde el extremo
inferior del tronco hasta la pared.
h → altura que alcanza el tronco apoyado en la pared.
x → distancia desde el extremo inferior del tronco hasta la pared.

9. La hipotenusa del triángulo que se forma mide 6,2 m, y un ángulo agudo, 55°.
h
Así: sen 55° = → h = 6,2 ⋅ sen 55° ≈ 6,2 ⋅ 0,82 = 5,08 m
6,2
El tronco se encuentra apoyado en la pared a 5,08 m del suelo.
x
cos 55° = → x = 6,2 ⋅ cos 55° ≈ 6,2 ⋅ 0,57 = 3,53 m
6,2
La distancia entre el extremo inferior del tronco y la pared es de 3,53 m.
23) Se quiere medir la altura de una estatua colocada en el centro de un lago circular. Para
ello, se mide la visual al extremo superior de la estatua desde el borde del lago y resulta
ser de 50°; nos alejamos 45 dm y volvemos a medir la visual, obteniendo un ángulo de 35°.
Averigua la altura de la estatua y la superficie del lago.
Hacemos una representación. Llamamos: h → altura de la estatua x → radio del lago
h 
tg 50° = → h = x ⋅ tg 50° 
x 
 → x ⋅ tg 50° = ( x + 45 ) ⋅ tg 35° →
h
tg 35° = → h = ( x + 45 ) ⋅ tg 35° 
x + 45 

→ x ⋅ 1,19 = ( x + 45 ) ⋅ 0,7 → 1,19 x = 0,7 x + 31,5 → 0,49 x = 31,5 → x = 64,29 dm
Luego h = 64,29 · 1,19 = 76,51 dm = 7,65 m
Calculamos la superficie del lago circular:
ACIRCULO = π ⋅ x 2 ≈ 3,14 ⋅ ( 64,29 ) ≈ 12978,26 dm2 ≈ 129,78 m2
2
La superficie del lago es de 129,78 m2.
24) Halla la altura de una antena sabiendo que a una distancia de 18 m se ve la parte superior
de la antena bajo un ángulo de 30°.
Llamamos h a la altura de la antena.
Como datos tenemos un ángulo y el cateto contiguo; nos piden el cateto opuesto al ángulo, luego la
tangente será la razón trigonométrica a usar:

10. h 3
tg 30° = → h = 18 ⋅ tg 30° = 18 = 6 3 ≈ 10,39 m
18 3
La altura de la antena es de 10,39 m.
25) El ángulo que se forma en la intersección de dos caminos es de 68 . La granja A está a
230 m de ese punto, y la granja B, a 435 m. ¿A qué distancia en línea recta está la granja
A de la granja B?
Llamamos x a la distancia en línea recta entre la granja A y la B.
Por no ser rectángulo el triángulo ABC, trazamos la altura h que lo divide en dos triángulos
rectángulos: AHC y AHB.
En el triángulo AHC conocemos C = 68° y AC = 230, podemos calcular h e y :
y
cos 68° = → y = 230 ⋅ cos 68° = 230 ⋅ 0,37 = 85,1 m
230
h
sen 68° = → h = 230 ⋅ sen 68° = 230 ⋅ 0,93 = 213,9 m
230
En el triángulo AHB, ahora conocemos h = 213,9 m y 435 − y = 435 − 85,1 = 349,9 m.
Podemos calcular x usando el teorema de Pitágoras:
x 2 = h 2 + ( 435 − y ) x 2 = ( 213,9 ) + ( 349,9 )
2 2 2
→ →
x = 45753,21 + 122 430,01 = 168183,22 ≈ 410,1 m
La distancia entre ambas granjas es de 410,1 m.