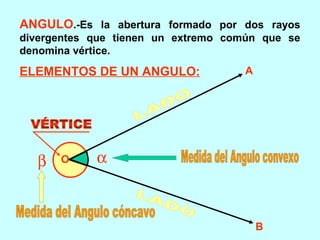
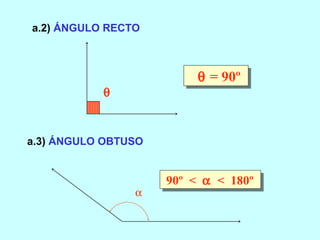
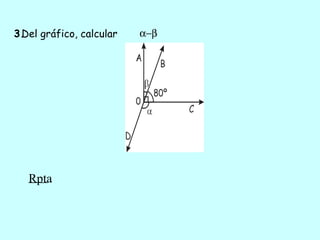
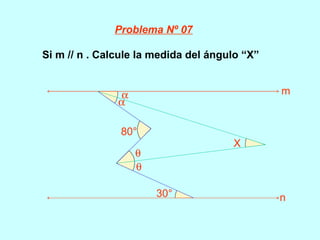
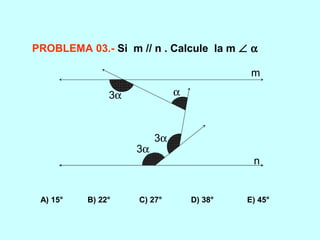
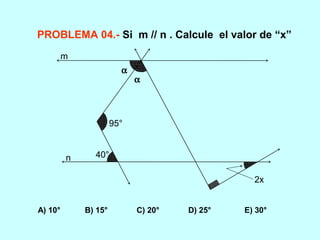
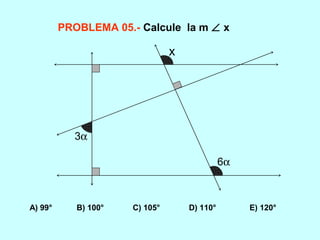
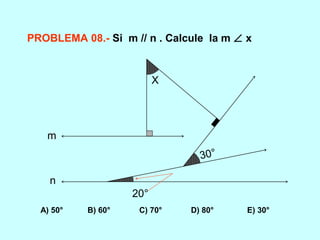
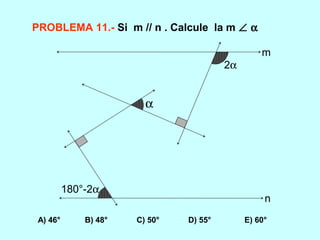
Este documento trata sobre los ángulos. Define qué es un ángulo y sus elementos principales. Explica las diferentes clasificaciones de los ángulos según su medida y suma. Luego presenta propiedades de los ángulos y problemas resueltos y propuestos relacionados con ángulos entre líneas paralelas y secantes.

1. ANGULOS
TEORIA
PROLEMAS RESUELTOS Y
PROPUESTOS
CARLOS ARBOLEDA BRUNO
ARBOLEDA_BRUNO@HOTMAL

2. β αO
A
B
ANGULO.-Es la abertura formado por dos rayos
divergentes que tienen un extremo común que se
denomina vértice.
ELEMENTOS DE UN ANGULO:

3. α
0º < α < 180º0º < α < 180º
0º < β < 90º0º < β < 90ºβ
CLASIFICACIÓN SEGÚN SU MEDIDA
a) ÁNGULO CONVEXO
a.1) ÁNGULO AGUDO

4. θ = 90ºθ = 90º
α
90º < α < 180º90º < α < 180º
θ
a.2) ÁNGULO RECTO
a.3) ÁNGULO OBTUSO

5. α + β = 90ºα + β = 90º
θ + δ = 180ºθ + δ = 180º
δθ
α
β
CLASIFICACIÓN SEGÚN SU SUMA
a) ÁNGULOS COMPLEMENTARIOS
b) ÁNGULOS SUPLEMENTARIOS

6. OTRAS FORMAS DE EXPRESIÓN
•Cα : Complemento de ; Cα = 90 – α
•Sα : Complemento de α ;Sα = 180 –
α .

7. α
β δ ε
φ
α α
CLASIFICACIÓN SEGÚN SU POSICIÓN
a) ÁNGULOS ADYACENTES b) ÁNGULOS CONSECUTIVOS
ÁNGULOS OPUESTOS POR EL VÉRTICE
Son congruentes
Puede formar más ángulosUn lado común

8. 01. Ángulos alternos internos:
m ∠3 = m ∠5; m ∠4 = m ∠6
02. Ángulos alternos externos:
m ∠1 = m ∠7; m ∠2 = m
∠8
03. Ángulos conjugados internos:
m ∠3+m ∠6=m ∠4+m ∠5=180°
04. Ángulos conjugados externos:
m ∠1+m ∠8=m ∠2+m ∠7=180°
05. Ángulos correspondientes:
m ∠1 = m ∠5; m ∠4 = m ∠8
m ∠2 = m ∠6; m ∠3 = m ∠7
ÁNGULOS ENTRE DOS RECTAS PARALELAS
Y UNA RECTA SECANTE
1 2
3
4
5 6
78

9. PROPIEDADES DE ÁNGULOS
Propiedad
Si: //
Entonces:
. x = α + β .

10. α + β + θ = x + yα + β + θ = x + y
α
β
θ
x
y
02.-Ángulos que se forman por una línea poligonal entre
dos rectas paralelas.
PROPIEDADES DE LOS ANGULOS

11. α
β
θ
δ
ε
α + β + θ + δ + ε = 180°α + β + θ + δ + ε = 180°
03.- ÁNGULOS ENTRE DOS RECTAS PARALELAS

12. α + β = 180°α + β = 180°
α β
04.- ÁNGULOS DE LADOS PERPENDICULARES

13. PROBLEMAS PROPUESTOS
1. ¿Cuánto es la diferencia de las medidas de los ángulos A0B y C0D, si
m∢BOD = 100º?
Rpta.

14. 2.Si: // //. Calcular x
Rpta.

15. 3.Del gráfico, calcular α−β
Rpta.

16. 4.-En la figura // // . Calcular xº
Rpta.

17. 5.-Según el gráfico: // . Calcular x

18. 6.-El complemento de α,
más el suplemento de 2α,
es igual al suplemento del
complemento de 3α.
Hallar α.
• 7.-Dos ángulos adyacentes
suplementarios difieren en
40º. Hallar la medida del
mayor ángulo.

19. • 8.-¿Cuánto mide un
ángulo si la diferencia
entre su suplemento y
su complemento es
seis veces el ángulo?
• 9.-Dos ángulos
complementarios están
en la relación de 3 a
2.Hallar la medida de
cada uno de estos
ángulos.

20. 10.-Hallar el suplemento del complemento de 20
11.-Hallar el complemento de un ángulo que mide el
doble de 16º.
12.-Halar el suplemento de la mitad de un ángulo
que mide 66º.

21. 13.-Se tiene los ángulos consecutivos , y , m∢A0C =
60º y
m∢BOD = 40º, m∢ = 80º. Hallar m∢ .
14.-Se tienen los ángulos consecutivos , y .m∢A0C =
50º, m∢B0D = 30º. Y m∢A0D = 70º Hallar m∢B0C

23. El complemento de la diferencia entre el suplemento
y el complemento de un ángulo “X” es igual al
duplo del complemento del ángulo “X”. Calcule la
medida del ángulo “X”.
90 - { ( ) - ( ) } = ( )180° - X 90° - X 90° - X2
90° - { 180° - X - 90° + X } = 180° - 2X
90° - 90° = 180° - 2X
2X = 180° X = 90°X = 90°
RESOLUCIÓN
Problema Nº 01
La estructura según el enunciado:
Desarrollando se obtiene:
Luego se reduce a:

24. La suma de las medidas de dos ángulos es 80° y el
complemento del primer ángulo es el doble de la
medida del segundo ángulo. Calcule la diferencia
de las medidas de dichos ángulos.
Sean los ángulos: α y β
α + β = 80°Dato: β = 80° - α ( 1 )
( 90° - α ) = 2β ( 2 )
Reemplazando (1) en (2):
( 90° - α ) = 2 ( 80° - α )
90° - α = 160° -2α
β = 10°
α = 70°
α - β = 70°-10°
= 60°
Problema Nº 02
RESOLUCIÓN
Dato:
Diferencia de las medidas
Resolviendo

25. La suma de sus complementos de dos ángulos es
130° y la diferencia de sus suplementos de los
mismos ángulos es 10°.Calcule la medida dichos
ángulos.
Sean los ángulos: α y β
( 90° - α ) ( 90° - β ) = 130°+
β + α = 50° ( 1 )
( 180° - α ) ( 180° - β ) = 10°-
β - α = 10° ( 2 )
Resolviendo: (1) y (2)
β + α = 50°
β - α = 10°
(+)
2β = 60°
β = 30°
α = 20°
Problema Nº 03
RESOLUCIÓN
Del enunciado:
Del enunciado:

26. Se tienen ángulos adyacentes AOB y BOC
(AOB<BOC), se traza la bisectriz OM del ángulo
AOC; si los ángulos BOC y BOM miden 60° y 20°
respectivamente. Calcule la medida del ángulo
AOB.
A B
O
C
M
α
α
60°
20°X
De la figura:
α = 60° - 20°
Luego:
X = 40° - 20°
α = 40°
X = 20°X = 20°
Problema Nº 04
RESOLUCIÓN

27. La diferencia de las medidas de dos ángulos
adyacentes AOB y BOC es 30°. Calcule la medida del
ángulo formado por la bisectriz del ángulo AOC con
el lado OB.
A
O
B
C
θ
θ
X
(θ- X)
( θ + X) (θ - X)= 30º
2X=30º
X = 15°X = 15°
Problema Nº 05
RESOLUCIÓN
M
Construcción de la gráfica según
el enunciado
Del enunciado:
AOB - OBC = 30°
-

28. Se tiene los ángulos consecutivos AOB, BOC y
COD tal que la m∠AOC = m∠BOD = 90°. Calcule
la medida del ángulo formado por las bisectrices
de los ángulos AOB y COD.
A
C
B
D
M
N
αα
β
β
θ
X
De la figura:
2α + θ = 90°
θ + 2β = 90°
( + )
2α + 2θ + 2β = 180°
α + θ + β = 90°
X = α + θ + βX = α + θ + β
X = 90°X = 90°
Problema Nº 06
RESOLUCIÓN
Construcción de la gráfica según el enunciado

29. Si m // n . Calcule la medida del ángulo “X”
80°
30°
α
α
θ
θ
X
m
n
Problema Nº 07

30. 2α + 2θ = 80° + 30°
Por la propiedad
Propiedad del cuadrilátero
cóncavo
α + θ = 55° (1)
80° = α + θ + X (2)
Reemplazando (1) en (2)
80° = 55° + X
X = 25°X = 25°
80°
30°
α
α
θ
θ
X
m
n
RESOLUCIÓN

31. Si m // n . Calcular la medida del ángulo “X”
5α
4α 65°
X
m
n
Problema Nº 08

32. 5α
4α 65°
X
m
n
Por la propiedad:
4α + 5α = 90°
α = 10°α = 10°
Ángulo exterior del triángulo
40° 65°
X = 40° + 65°
X = 105°X = 105°
RESOLUCIÓN

33. Si m // n . Calcule la medida del ángulo ”X”
α
2α
x
m
n
θ
2θ
Problema Nº 01

34. 3α + 3θ = 180°
α + θ = 60°α + θ = 60°
Ángulos entre líneas poligonales
X = α + θ X = 60°X = 60°
RESOLUCIÓN
α
2α
x
m
n
θ
2θ
x
Ángulos conjugados
internos

36. PROBLEMA 01.- Si L1 // L2 . Calcule la m ∠ x
A) 10° B) 20° C) 30° D) 40° E) 50°
x
α
α
β
β
4x
3x
L1
L2

37. m
n
30°
X
PROBLEMA 02.- Si m // n . Calcule la m ∠ x
A) 18° B) 20° C) 30° D) 36° E) 48°

38. PROBLEMA 03.- Si m // n . Calcule la m ∠ α
A) 15° B) 22° C) 27° D) 38° E) 45°
3α
3α
3α
α
m
n

39. PROBLEMA 04.- Si m // n . Calcule el valor de “x”
A) 10° B) 15° C) 20° D) 25° E) 30°
40°
95°
α
α
2x
m
n

40. PROBLEMA 05.- Calcule la m ∠ x
A) 99° B) 100° C) 105° D) 110° E) 120°
3α
6α
x

41. α
4θ
4α
θ
X
m
n
PROBLEMA 06.- Si m // n . Calcule la m ∠ x
A) 22° B) 28° C) 30° D) 36° E) 60°

42. A) 24° B) 25° C) 32° D) 35° E) 45°
PROBLEMA 07.- Si. Calcule la m ∠ x
88°
24°
x
α
α
θ
θ
m
n

43. PROBLEMA 08.- Si m // n . Calcule la m ∠ x
20°
30°
X
m
n
A) 50° B) 60° C) 70° D) 80° E) 30°

44. PROBLEMA 09.-Si m//n y θ- α = 80°. Calcule la m∠x
A) 60° B) 65° C) 70° D) 75° E) 80°
θ
θ
x
α
α
m
n

45. PROBLEMA 10.- Si m // n . Calcule la m ∠ x
A) 20° B) 30° C) 40° D) 50° E) 60°
x
x
x
m
n

46. PROBLEMA 11.- Si m // n . Calcule la m ∠ α
A) 46° B) 48° C) 50° D) 55° E) 60°
180°-2α
α
2α
m
n

47. PROBLEMA 12.- Si m // n . Calcule la m ∠ x
A) 30° B) 36° C) 40° D) 45° E) 50°
α
α
θ
θ
x
80°
m
n

48. PROBLEMA 13.- Si m // n . Calcule la m ∠ x
A) 30° B) 40° C) 50° D) 60° E) 70°
80°
α
α
β
β
m
n
x

49. REPUESTAS DE LOS PROBLEMAS PROPUESTOS
1. 20º 8. 50º
2. 30º 9. 80º
3. 45º 10. 30º
4. 10º 11. 60º
5. 120º 12. 40º
6. 36º 13. 50º
7. 32º