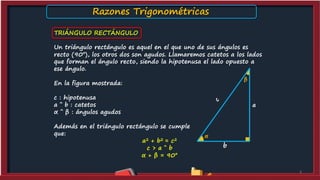
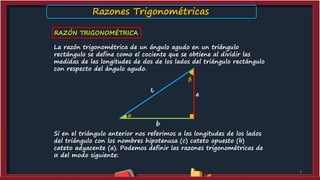
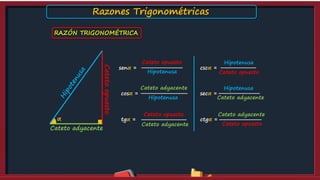
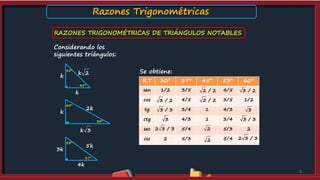
Este documento presenta información sobre las razones trigonométricas. Explica qué es un triángulo rectángulo y define las razones trigonométricas en términos de los lados del triángulo. Luego proporciona ejemplos numéricos para calcular las razones trigonométricas. También cubre las razones trigonométricas de ángulos complementarios y ejercicios de práctica.

1. 1
ALUMNO:
Gabriel de Jesús Alvarenga Cardoza
MATERIA:
Matemática
GRADO:
Primer Año De Bachillerato General.
SECCION:
“A”.
AÑO :
2018.
INSTITUTO NACIONAL DE SAN RAFAEL

2. 2
Razones
Trigonométricas

3. TRIÁNGULO RECTÁNGULO
Un triángulo rectángulo es aquel en el que uno de sus ángulos es
recto (90°), los otros dos son agudos. Llamaremos catetos a los lados
que forman el ángulo recto, siendo la hipotenusa el lado opuesto a
ese ángulo.
En la figura mostrada:
c : hipotenusa
a ˆ b : catetos
α ˆ β : ángulos agudos
Además en el triángulo rectángulo se cumple
que:
a2 + b2 = c2
c > a ˆ b
α + β = 90°
3
a
b
β
α
Razones Trigonométricas

4. RAZÓN TRIGONOMÉTRICA
La razón trigonométrica de un ángulo agudo en un triángulo
rectángulo se define como el cociente que se obtiene al dividir las
medidas de las longitudes de dos de los lados del triángulo rectángulo
con respecto del ángulo agudo.
Si en el triángulo anterior nos referimos a las longitudes de los lados
del triángulo con los nombres hipotenusa (c) cateto opuesto (b)
cateto adyacente (a). Podemos definir las razones trigonométricas de
α del modo siguiente:
4
a
b
β
α
Razones Trigonométricas

5. senα =
Hipotenusa
Cateto opuesto
Hipotenusa
Cateto adyacente
cosα =
Cateto adyacente
Cateto opuesto
tgα =
cscα =
Hipotenusa
Cateto opuesto
Hipotenusa
Cateto adyacente
secα =
Cateto adyacente
Cateto opuesto
ctgα =
Catetoopuesto
Cateto adyacente
α
RAZÓN TRIGONOMÉTRICA
Razones Trigonométricas

6. Ejempl0 1
Halla las razones trigonométricas del menor ángulo de un triángulo
rectángulo, si la hipotenusa mide 5m y uno de los catetos mide 3m.
Solución
Para poder calcular las seis razones trigonométricas necesitamos hallar
la medida del otro cateto; esto lo hacemos aplicando el Teorema de
Pitágoras. Una vez hallado el valor de este cateto, procedemos a
encontrar los valores de las razones por medio sus respectivas
definiciones.
α
5
3
3
sen
5
α 
4
cos
5
α 
3
tan
4
α 
5
csc
3
α 
5
sec
4
α 
4
cot
3
α 
4
Razones Trigonométricas

7. Ejempl0 2
Se tiene un triángulo rectángulo cuyos catetos miden 8 y 15m. Halla
las razones trigonométricas del mayor ángulo agudo.
Solución
Primero hallamos el valor de la hipotenusa, aplicando el Teorema de
Pitágoras; luego, calculamos las razones trigonométricas, a partir de sus
respectivas definiciones y con los datos dados y obtenidos:
15
sen
17
α 
8
cos
17
α 
15
tan
8
α 
17
csc
15
α 
17
sec
8
α 
8
co t
15
α 
α
8
15
17
Razones Trigonométricas

8. RAZONES TRIGONOMÉTRICAS DE TRIÁNGULOS NOTABLES
Considerando los
siguientes triángulos:
8
k
k 2
k
45°
45°
2k
k 3
k
30°
60°
5k
4k
3k
37°
53°
R.T 30° 37° 45° 53° 60°
sen 1/2 3/5 4/5
cos 4/5 3/5 1/2
tg 3/4 1 4/3
ctg 4/3 1 3/4
sec 5/4 5/3 2
csc 2 5/3 5/4
2 / 2 3 / 2
3 / 2 2 / 2
Se obtiene:
3 / 3 3
3 3 / 3
2 3 / 3 2
2 2 3 / 3
Razones Trigonométricas

9. EJERCICIOS PARA LA CLASE
01. En un triángulo rectángulo ABC (recto en B); calcular:
E = 2tanA.tanC + 3cosA.cscC
02. En un triángulo rectángulo ABC (recto en C); reducir:
03. En un triángulo rectángulo, los lados de menor longitud miden 2 y 3cm.
Si el mayor de los ángulos agudos mide “”; calcular:
04. En un triángulo rectángulo ABC recto en A se sabe que: b + c = 14 y
senB.senC = 0,48. Calcular la longitud de la hipotenusa.
05. En un triángulo ABC (B = 90º), se sabe que: secA = 2,6. Si el perímetro
del triángulo es 60cm, ¿cuál es su área?
9
2c.cosB b.tanA
E
a c.senA
+
=
+
2 5
E 2sen β
13
= -
Razones Trigonométricas

10. RAZONES TRIGONOMÉTRICAS RECÍPROCAS
10
Son recíprocas, aquellos pares de razones trigonométricas de un mismo
ángulo, que al multiplicarse entre si resultan la unidad. Se definen la
cosecante, la secante y la cotangente, como las razones recíprocas (inversas)
al seno, coseno y tangente, del siguiente modo:
La cosecante es la razón recíproca del seno, o su inverso multiplicativo:
La secante es la razón recíproca del coseno, o su inverso multiplicativo:
La cotangente es la razón recíproca del tangente, o su inverso multiplicativo:
1
csc
s en
α
α
 s en . csc 1α α 
1
sec
cos
α
α
 cos . s e c 1α α 
tg . c tg 1α α 
1
ctg
tg
α
α

Razones Trigonométricas

11. EJERCICIOS PARA LA CLASE
06. Sabiendo que sen(2x + 15)° . csc65° = 1, halla el valor de x
07. Si cos(3x + 10)°. sec(x + 70)° = 1, calcula el valor de x
08. Halla el valor de x si tg(5x – 50)° . ctg(4x + 20)° = 1
09. Si se cumple que: cos(7x2 – 3)° . sec(2x + 9)° = 1
10. Calcula x e y en:
11
sen(3x 2y 30) . csc(x y 10) 1
tg(5x y 20) .ctg(x 2y 30) 1
ìï + - ° - + ° =ï
í
ï + + ° + + ° =ïî
Razones Trigonométricas

12. RAZONES TRIGONOMÉTRICAS DE ÁNGULOS COMPLEMENTARIOS
12
Dos ángulos agudos se llaman complementarios si su suma es un
ángulo recto (90°).
En la figura se muestra:
α ˆ β : Son ángulos complementarios (α + β = 90º)
Hemos nombrado el ángulo opuesto al cateto a como α y al ángulo
opuesto al cateto b como β en consecuencia:
a
b
β
α
Razones Trigonométricas

13. senα =
c
a
cosα =
c
b
α
β
c
a
b
tgα =
b
a
ctα =
a
b
secα =
b
c
cscα =
a
c
b
a
ctgβ =
tgβ =
a
b
cscβ =
b
c
secβ =
a
c
senβ =
c
b
cosβ =
c
a
cosα = senβ
senα = cosβ
ctgα = tgβ
tcgα = tgβ
cscα = secβ
secα = cscβ
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS COMPLEMENTARIOS
“Las razones trigonométricas de todo ángulo agudo son respectivamente
iguales a las co-razones trigonométricas de su ángulo complementario”
Razones Trigonométricas

14. RAZONES TRIGONOMÉTRICAS DE ÁNGULOS COMPLEMENTARIOS
Ejemplos:
sen 25° = cos 65° porque 25° + 65° =
90°
tg 50° = ctg 40° porque 50° + 40° =
90°
sec 12° = csc 78° porque 12° + 78° = 90°
Ejercicio 1
Halla el valor de θ en:
Sen 2θ = Cos 84°
Solución
Dado que deben ser ángulos
complementarios:
 2θ + 84° = 90°
 2θ = 6°
 θ = 3°
Ejercicio 2
Halla el valor de θ en:
tg 5α = ctg α
Solución
Dado que deben ser ángulos
complementarios:
 5α + α = 90°
 6α = 90°
 α = 15°
Razones Trigonométricas

15. EJERCICIOS PARA LA CLASE
11. Si sen(3x + 10)° = cos(2x + 53)° , calcula el valor de x
12. Si sec(5x – 40)° = csc(2x – 10)°, halla el valor de x
13. Si tg(2x + 15)° . tg51° = 1, halla el valor de x
14. Siendo: . Halla el valor de x (x є Z+)
15. Calcula x e y en:
15
2
tg(x 5x 1)
1
ctg(6x 11)
+ - °
=
+ °
sen(2x y 8) cos(x 2y 16)
sec(2x 3y 8) csc(x y 20)
ìï + + ° = + + °ï
í
ï + - ° = + + °ïî
Razones Trigonométricas

16. Razones Trigonométricas
http://www.librosvivos.net/smtc/homeTC.asp?temaclave=1173