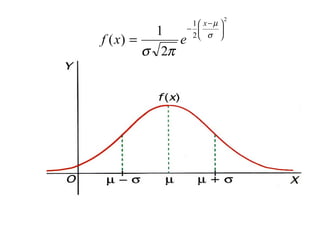
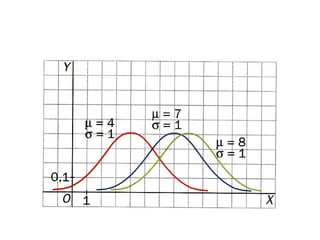
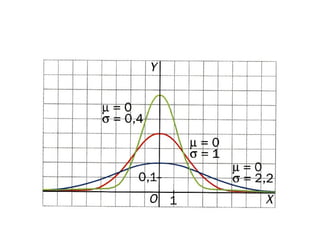
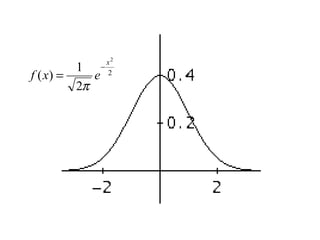
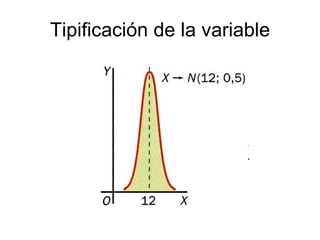
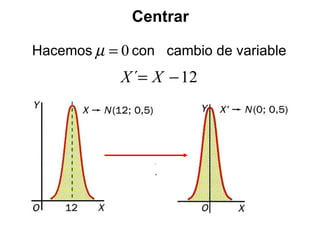
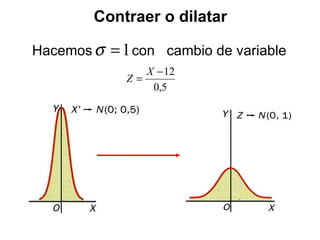
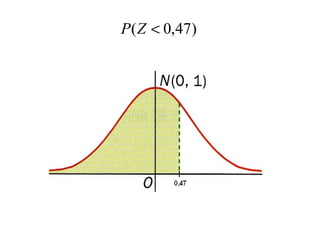
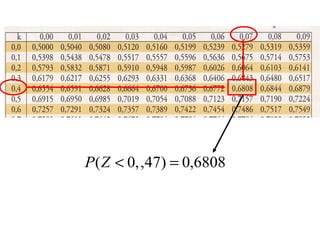
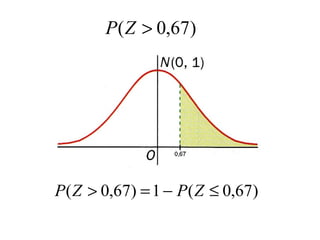
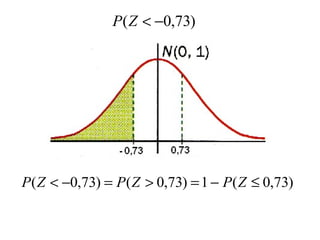
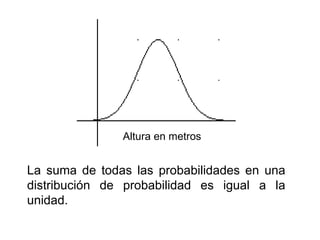
El documento describe diferentes tipos de distribuciones de probabilidad, incluyendo distribuciones discretas como la binomial y distribuciones continuas como la normal. Explica conceptos clave como función de probabilidad, media, varianza, función de densidad y función de distribución. También proporciona ejemplos para ilustrar estos conceptos estadísticos fundamentales.

1. DISTRIBUCIONES DE PROBABILIDAD

2. DISTRIBUCIONES DISCRETAS DE PROBABILIDAD

3. Variable aleatoria Definición: Se llama variable aleatoria a toda función que asocia a cada elemento del espacio muestral un número real X : E R

4. Ejemplo: Consideremos el experimento consistente en el lanzamiento de dos monedas. El espacio muestral asociado será

5. Asignamos a cada elemento del espacio muestral un número, el correspondiente al número de caras.

6. Función de probabilidad Definición: Se llama función de probabilidad de una variable aleatoria X a la función que asocia a cada valor x de la variable su probabilidad

7. Ejemplo: Consideremos el experimento consistente en el lanzamiento de un dado perfecto. Tendremos la siguiente situación :

8. Se debe cumplir que X Función de probabilidad p 1 1/6 2 1/6 3 1/6 4 1/6 5 1/6 6 1/6

10. Función de distribución Definición: Sea X una variable aleatoria discreta cuyos valores suponemos ordenados de menor a mayor. Llamamos función de distribución de la variable X a la función

11. Ejemplo: Consideremos el experimento consistente en el lanzamiento de un dado perfecto. Tendremos la siguiente situación:

12. X p F 1 1/6 1/6 2 1/6 2/6 3 1/6 3/6 4 1/6 4/6 5 1/6 5/6 6 1/6 1

14. M edia Definición: Se llama media de la variable aleatoria X , que toma valores con probabilidades al valor:

15. Ejemplo: En el ejemplo del lanzamiento del dado perfecto tendremos:

16. Desviación Típica Definición: Se llama desviación típica de la variable aleatoria X , a la raíz cuadrada positiva de la varianza:

17. DISTRIBUCIÓN BINOMIAL

18. Un experimento aleatorio con las siguientes características sigue el modelo de una distribución binomial a) En cada prueba del experimento sólo son posibles dos resultados. b) El resultado de cada prueba es independiente de los anteriores. c) La probabilidad de cada uno de los dos sucesos posibles permanece constante

19. Variable aleatoria bino m ial Definición: Representamos por p la probabilidad de un suceso A (éxito) y por q la probabilidad del contrario de A (fracaso). A la variable X que representa el número de éxitos la llamamos variable aleatoria binomial .

20. Esta distribución la representamos como: siendo n y p los parámetros de la misma

21. Ejemplo: Una compañía de tabaco ha determinado que el porcentaje de fumadores en una ciudad es del 35%. Se escoge al azar una muestra formada por 10 personas. La variable que representa el número de fumadores dentro de la muestra sigue una distribución binomial .

22. Función de probabilidad Se puede demostrar que en una distribución , la probabilidad de obtener r éxitos viene dada por: que es la función de probabilidad de la distribución binomial.

23. Ejemplo : Una prueba de inteligencia está compuesta de 10 preguntas, cada una de las cuales tiene 4 respuestas, siendo sólo una de ellas correcta. Si se contesta aleatoriamente se pide:

24. a) Probabilidad de acertar 4 preguntas Se trata de una distribución binomial con , , n =10 y r =4

25. b) Probabilidad de no acertar ninguna En este caso r=0:

26. M edia y Varianza Se puede demostrar que para una distribución binomial la media y la varianza vienen dadas por :

27. Ejemplo : Una prueba de inteligencia está compuesta de 10 preguntas, cada una de las cuales tiene 4 respuestas, siendo sólo una de ellas correcta. Si se contesta aleatoriamente se pide:

28. DISTRIBUCIONES CONTINUAS DE PROBABILIDAD

29. La variable aleatoria asociada a una distribución de probabilidad puede tomar un número infinito de valores dentro de un intervalo, también puede ser que tome un número finito de valores, pero muy elevado o ser infinito y agruparse en intervalos. En todos estos casos tendremos una distribución continua de probabilidad

30. Ejemplo: Se miden las tallas de los alumnos varones de 2º de Bachillerato, obteniéndose la siguiente tabla de frecuencias:

32. Podemos suponer que la distribución de tallas de los alumnos varones de toda España, a medida que los intervalos se hacen más pequeños, tiende al diagrama siguiente:

33. Altura en metros La suma de todas las probabilidades en una distribución de probabilidad es igual a la unidad.

34. Función de densidad Definición: Una función que cumple: a) b) El área encerrada bajo la curva es igual a la unidad Se denomina función de densidad de una variable aleatoria continua X

35. Función de distribución Definición : Sea f(x) una función de densidad de una variable aleatoria continua X, y F(x) una función que cumple las condiciones: a) b) situado a la izquierda del menor valor de la variable. c) situado a la derecha del mayor valor de la variable La función F(x) se denomina función de distribución de la variable aleatoria X .

36. F(x) representa la probabilidad de que la variable aleatoria tome un valor menor o igual que x,

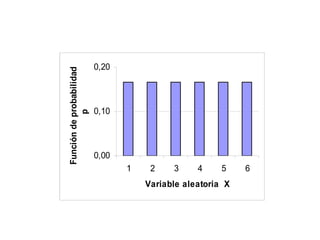
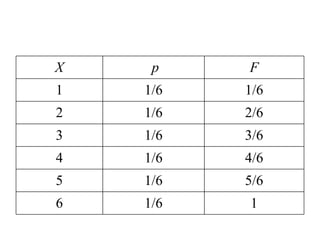
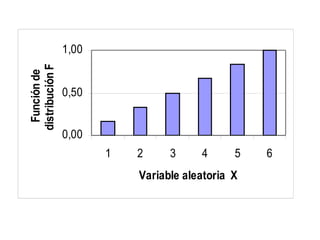
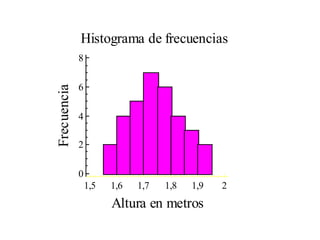
37. Media de una variable aleatoria continua Definición: Sea X una variable aleatoria continua, cuyo recorrido es el intervalo [ a,b ] y sea f(x) su función de densidad. Se llama media de la variable continua X al valor: También se llama esperanza matemática o valor esperado.

38. Varianza de una variable aleatoria continua Definición: Se llama varianza de una variable aleatoria continua al valor de la siguiente integral: la desviación típica es la raíz cuadrada de la varianza

39. DISTRIBUCIÓN NORMAL

40. Entre las distribuciones continuas, la más importante es la distribución normal o de Gauss. Son distribuciones cuya representación se aproxima a la siguiente gráfica

41. Variable aleatoria Frecuencia

42. Son curvas llamadas "campanas de Gauss".que tienen las siguientes características: a) En una distribución normal media, moda y mediana coinciden en el máximo de la curva b) El área encerrada bajo la campana y el eje x es igual a la unidad. c) Los puntos de inflexión son los puntos y

48. Tipificación de la variable

49. Centrar Hacemos con cambio de variable

50. Contraer o dilatar Hacemos con cambio de variable