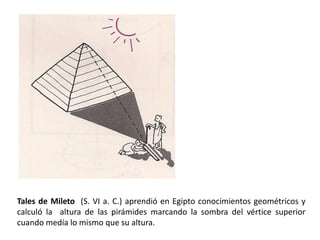
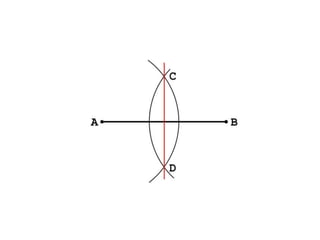
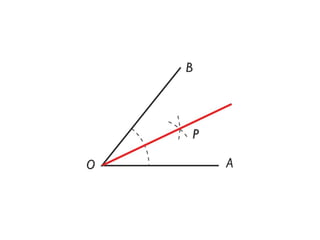
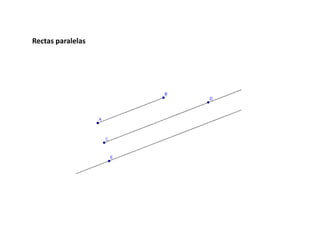
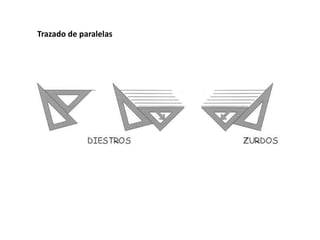
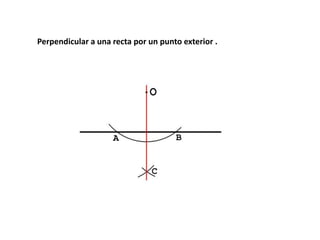
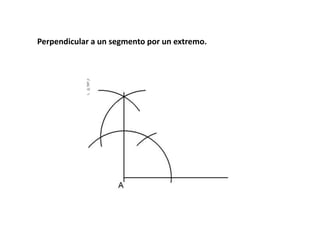
Este documento trata sobre la geometría y sus elementos básicos. Explica que la geometría estudia las propiedades y medidas de las figuras geométricas en el plano y el espacio, las cuales se componen de elementos como puntos, líneas, curvas y superficies. Luego describe algunos de estos elementos geométricos fundamentales como la circunferencia, la mediatriz, la bisectriz y las líneas paralelas, y presenta métodos para trazar estas figuras.

1. Educación Plástica y Visual
1º EVALUACIÓN: LA GEOMETRÍA

2. Geometría
La geometría es una parte de la matemática que se ocupa del
estudio de propiedades y medidas de las figuras geométricas, en el
plano o en el espacio. Estas figuras se conforman de elementos
geométricos que son: puntos, planos, rectas paralelas y
perpendiculares, curvas, superficies, etc. La geometría tiene su
origen en el antiguo Egipto.

3. Tales de Mileto (S. VI a. C.) aprendió en Egipto conocimientos geométricos y
calculó la altura de las pirámides marcando la sombra del vértice superior
cuando medía lo mismo que su altura.

4. ELEMENTOS GEOMÉTRICOS
Los elementos geométricos son aquellos de cuya combinación obtenemos
las figuras geométricas, también los llamamos lugar geométrico de los
puntos por ser un conjunto de puntos que cumplen unas propiedades
geométricas determinadas respecto a otro punto o elemento geométrico.
Distinguimos:

5. 1. lugares geométricos del plano:
• Circunferencia: lugar geométrico de los puntos del plano que
equidistan (tienen la misma distancia) de otro punto llamado centro.

9. 1. lugares geométricos del plano:
• Circunferencia: lugar geométrico de los puntos del plano que
equidistan (tienen la misma distancia) de otro punto llamado centro.
• Mediatriz: lugar geométrico de los puntos del plano que equidistan de
los extremos de un segmento.

11. 1. lugares geométricos del plano:
• Circunferencia: lugar geométrico de los puntos del plano que
equidistan (tienen la misma distancia) de otro punto llamado centro.
• Mediatriz: lugar geométrico de los puntos del plano que equidistan de
los extremos de un segmento.
• Bisectriz: lugar geométrico de los puntos del plano que equidistan de
los lados de un segmento.

13. 1. lugares geométricos del plano:
• Circunferencia: lugar geométrico de los puntos del plano que
equidistan (tienen la misma distancia) de otro punto llamado centro.
• Mediatriz: lugar geométrico de los puntos del plano que equidistan de
los extremos de un segmento.
• Bisectriz: lugar geométrico de los puntos del plano que equidistan de
los lados de un segmento.
• Paralela: lugar geométrico de los puntos del plano que equidistan de
otra recta.

14. Rectas paralelas

15. Captura de un segmento
1. Trazamos una recta desde un punto A´.
2. Tomamos la medida AB con el compás.
3. Trasladamos con el compás la distancia AB a la recta que hemos trazado,
pinchando en A´, trazamos B´.

16. Trazado de paralelas

17. Paralela a una recta por un punto exterior.
1. Se elige un punto X cualquiera centrado en la recta. La distancia entre este
punto X y el punto dado A, será el radio. Con este radio trazamos una
circunferencia que cortará la recta en los puntos 1 y 2.
2. Con centro en 1 y radio A2 se traza un arco que corte al anterior arco. Este
corte será el punto B.
3. Trazamos la recta que une los puntos A y B. Esta recta es la paralela que
buscamos.

18. Paralela a una recta por un punto exterior.

19. Trazado de perpendiculares.

20. Perpendicular a una recta por un punto exterior .
1. Con centro en A y radio cualquiera trazamos un arco que corte la recta en
los puntos 1 y 2.
2. Desde 1, con un radio mayor a la mitad de la distancia a 2, trazamos un arco
de abajo arriba. Repetimos la acción desde 2. El corte de ambos arcos será
B.
3. Trazamos la recta que une los puntos A y B. Esta recta es la perpendicular
que buscamos.

21. Perpendicular a una recta por un punto exterior .

22. Perpendicular a un segmento por un extremo.
1. Con centro en A y radio cualquiera trazamos un arco que corte el segmento
AB en el punto C.
2. Con el mismo radio desde C, se traza otro arco que pasando por A corta al
anterior en D. Repetimos la acción con centro en D, cortando el primer arco
en el punto E.
3. Siguiendo con el mismo radio trazamos un arco desde E, y desde D, otro que
corte a este en F. La recta que une F y A es la perpendicular .

23. Perpendicular a un segmento por un extremo.