Este documento presenta el tema 1 de las matemáticas aplicadas a las ingenierías aeroespacial, civil y química. Introduce las cónicas y cuadráticas, comenzando con las secciones cónicas y definiendo las propiedades de la parábola, elipse e hipérbola a través de definiciones métricas. Explica cómo adoptar sistemas de coordenadas para obtener ecuaciones implícitas simplificadas para cada curva, identificando sus elementos característicos como el foco, directriz y ejes

1. Ingenier´ıas: Aeroespacial, Civil y Qu´ımica.
Matem´aticas I. 2010-2011.
Departamento de Matem´atica Aplicada II.
Escuela Superior de Ingenieros. Universidad de Sevilla.
Tema 1.- C´onicas y Cu´adricas.
1.1.- Las c´onicas. Ecuaciones reducidas.
Las secciones c´onicas.
Definici´on m´etrica y elementos notables.
La propiedad focal.
Ecuaci´on reducida de una c´onica no girada.
Ecuaciones param´etricas.
1.2.- Las cu´adricas. Ecuaciones reducidas.
Ecuaci´on reducida de una cu´adrica no girada.
Los elipsoides.
Los hiperboloides y el cono.
Los paraboloides.
Los cilindros y las cu´adricas degeneradas.
1.3.- Ejercicios.
1.4.- Ap´endice: MATLAB.
È
r2 − (x − a)2,
Referente a la geometr´ıa del plano, el alumno conoce, de sus estudios de bachillerato,
las curvas que se obtienen como gr´afica de una funci´on expl´ıcita, y = f(x). Adem´as, conoce
la ecuaci´on general (o impl´ıcita) de la recta ax + by + c = 0, ecuaci´on que salvo casos
excepcionales (b = 0) define a y como funci´on expl´ıcita de x, y = −1
(ax+c). Por otra parte,
b conoce la circunferencia, curva que no puede obtenerse como gr´afica de una funci´on expl´ıcita.
La relaci´on que establece la ecuaci´on de una circunferencia (x − a)2 + (y − b)2 = r2 entre
las variables (x, y) es una relaci´on impl´ıcita. Podemos obtener expresiones expl´ıcitas de y en
funci´on de x si dividimos la circunferencia en dos semi-circunferencias y = b±
pero el trabajar con estas expresiones obliga a no poder considerar y hacer c´alculos sobre la
curva completa.
En este tema estudiaremos las ecuaciones y los aspectos elementales de las c´onicas (cur-
vas planas de segundo grado) y las cu´adricas (las superficies de segundo grado). En dicho
tratamiento elemental consideraremos las propiedades intr´ınsecas (propiedades que no depen-
den del sistema de coordenadas) y estudiaremos las ecuaciones de dichas curvas y superficies
cuando sus elementos de simetr´ıa son paralelos a alguno de los ejes o planos coordenados. M´as
adelante, en la parte final de la asignatura, con las herramientas correspondientes al c´alculo
de autovalores y autovectores y a la diagonalizaci´on ortogonal de una matriz sim´etrica real,
podr´a completarse el estudio considerando las c´onicas y cu´adricas dadas por su ecuaci´on en
forma general.
1

2. 2 Tema 1.- C´onicas y Cu´adricas.
1.1.- Las c´onicas. Ecuaciones reducidas.
En primer lugar vamos a estudiar los aspectos b´asicos de las c´onicas no degeneradas
(par´abola, elipse e hip´erbola), considerando la definici´on de ´estas como el lugar geo-
m´etrico de todos los puntos del plano que verifican una determinada propiedad m´etrica.
Independientemente de que el resultado sea o no sea una c´onica, algunos ejemplos sencillos
de lugares geom´etricos definidos mediante condiciones m´etricas son los siguientes:
La circunferencia: lugar geom´etrico de los puntos de un plano que est´an a una distancia
prefijada de un punto fijo,
La mediatriz de un segmento: el lugar geom´etrico de los puntos de un plano que
equidistan de los extremos del segmento,
El lugar geom´etrico de los puntos que equidistan de dos rectas que se cortan est´a for-
mado por las dos bisectrices de los ´angulos que determinan las rectas dadas,
Una vez definida cada c´onica, veremos que, adoptando un sistema de ejes adecuado, ´esta
queda caracterizada mediante una ecuaci´on impl´ıcita en dos variables (x, y) que vendr´a dada
por una ecuaci´on polin´omica de segundo grado sin t´ermino en xy.
Adem´as de las ecuaciones impl´ıcitas de las distintas c´onicas (referidas a ejes apropiados)
consideraremos una descripci´on param´etrica. En t´erminos generales, puede decirse que las
descripciones param´etricas son las herramientas m´as apropiadas a la hora de representar
gr´aficamente una curva (plana o tridimensional) o una superficie. Esto se pone de manifiesto
a la hora de obtener las gr´aficas de curvas y superficies usando MATLAB (o cualquier otro
paquete de programas que permita representar gr´aficamente curvas y superficies definidas
mediante ecuaciones).
1.1.1.- Las secciones c´onicas.
Dejando al margen coordenadas, ecuaciones,...el nombre completo de las c´onicas es el
de secciones c´onicas pues son las curvas que se obtienen al seccionar un cono mediante
un plano. El tipo de curva que se obtiene al cortar un cono circular recto (m´as adelante
obtendremos su ecuaci´on) con un plano depende de si el plano pasa o no por el v´ertice del
cono y de la relaci´on entre el ´angulo, 0 ≤ ≤
, de inclinaci´on del plano respecto al eje del
2 cono y el ´angulo, 0

3. 2 , de inclinaci´on de la recta generatriz del cono respecto del eje.
Tenemos los siguientes casos:
• Un punto, concretamente el v´ertice del cono, si cortamos con un plano que pasa por el
v´ertice y

4. ≤
2 .
• Dos rectas secantes, si cortamos con un plano que pasa por el v´ertice y 0 ≤

5. .
• Una recta doble, si cortamos con un plano que pasa por el v´ertice y =

6. .
• Una elipse, si cortamos con un plano que no pase por el v´ertice del cono y

7. ≤
2 . En
particular, si cortamos con un plano perpendicular al eje del cono ( =
2 ), se obtiene
una circunferencia.
• Una par´abola, si cortamos con un plano que no pase por el v´ertice y sea paralelo a una
generatriz, =

8. .
• Una hip´erbola, si cortamos con un plano que no pase por el v´ertice y 0 ≤

9. .
Matem´aticas I. 2Ingenier´ıas: Aeroespacial, Civil y Qu´ımica

10. 1.1- Las c´onicas. Ecuaciones reducidas. 3
Un punto Una recta doble
Dos rectas que se cortan
Elipse
Circunferencia
Par´abola
Hip´erbola
1.1.2.- Definici´on m´etrica y elementos notables.
Vamos a definir (cada una de) las c´onicas como el conjunto de puntos del plano que
verifican una determinada propiedad m´etrica (referida a distancias). Adoptando un sistema
de referencia adecuado, obtendremos la ecuaci´on impl´ıcita correspondiente y las coordenadas
y ecuaciones de los elementos distintivos (centro, ejes,...) que tenga en cada caso.
• La par´abola.
Aunque sea una curva plana conocida por el alumno como la gr´afica de una funci´on
polin´omica de segundo grado y = f(x) = ax2 + bx + c y como la trayectoria descrita por un
proyectil, adoptaremos ahora otro punto de vista.
Definici´on. Dada una recta L y un punto F (que no est´e en L), se denomina par´abola
de foco F y directriz L al lugar geom´etrico de los puntos P (del plano determinado por
la directriz y el foco) que equidistan de la directriz L y el foco F,
d (P, L) = d (P, F).
Ejercicio. ¿Qu´e sucede si el punto F est´a en la recta L?
Matem´aticas I. 3 2010-2011

11. 4 Tema 1.- C´onicas y Cu´adricas.
En la definici´on considerada no hay ninguna referencia a sistema de coordenadas alguno.
En el plano determinado por la recta y el punto dados, vamos a considerar un sistema de
referencia adecuado, de forma que la ecuaci´on que caracterice a los puntos de la par´abola
sea lo m´as sencilla posible. Como eje OX, de la variable independiente, vamos a tomar la
recta que pasa por el foco F y es perpendicular a la directriz L. Como origen del sistema de
referencia tomamos el punto O de dicha recta que equidista del foco y de la directriz. Por
´ultimo, como eje OY de nuestro sistema de referencia tomamos la recta que pasa por O y
es paralela a la directriz.
En este sistema de ejes perpendiculares tendremos que las coordenadas del foco ser´an de
la forma F = ( p
2 , 0) y la ecuaci´on de la directriz ser´a L ≡ x = −p
2 . U n punto P = (x, y)
pertenecer´a a la par´abola definida si y s´olo si
d (P, L) =

15. x +
p
2

19. = d (P, F) =
r
(x −
p
2
)2 + y2.
De aqu´ı es f´acil obtener que los puntos
(x, y) que est´an en la par´abola est´an
caracterizados por la ecuaci´on
y2 = 2p x |p| = d (F, L).
La recta y = 0 (el eje OX) es eje de
simetr´ıa de la par´abola anterior y el
v´ertice (el punto de corte del eje de
simetr´ıa con la par´abola) es el origen
de coordenadas O = (x = 0, y = 0).
y2 = 2p x
X
Y
Foco
Eje de simetr´ıa
F = (
p
2
, 0)
V´ertice
O
directriz
x = −
p
2
P = (x, y)
El eje de simetr´ıa de una par´abola tambi´en se suele llamar eje focal. La recta que pasa
por el v´ertice y es perpendicular al eje de simetr´ıa se suele llamar eje secundario de la
par´abola.
Una ecuaci´on del tipo x2 = 2q y define una par´abola con eje de simetr´ıa el eje OY y
v´ertice en el origen de coordenadas.
Si cuando hemos obtenido la ecuaci´on de la
par´abola, y2 = 2p x, hubieramos adoptado
un sistema de ejes paralelo al que hemos
adoptado (o lo que es lo mismo si hacemos
una traslaci´on del sistema de coordenadas),
en el cual el eje OX sea paralelo al eje de
simetr´ıa de la par´abola (dicho eje de simetr´ıa
tendr´ıa como ecuaci´on y =

20. ) y el v´ertice tu-
viera como coordenadas (,

21. ), la ecuaci´on
de la par´abola en dicho sistema de coorde-
nadas ser´ıa de la forma
Y
V´ertice (,

22. )
Eje
y =

23. O
x =
(y −

24. )2 = 2p (x − )
(y −

25. )2 = 2p (x − ). X
Ejercicio. Determina el v´ertice, el eje de simetr´ıa, el foco y la directriz de las par´abolas
(y −

26. )2 = 2p (x − ), (x − )2 = 2q (y −

27. ).
Matem´aticas I. 4Ingenier´ıas: Aeroespacial, Civil y Qu´ımica

28. 1.1- Las c´onicas. Ecuaciones reducidas. 5
Las ecuaciones anteriores cubren todos los casos en los que el eje de la par´abola es paralelo
a uno de los ejes coordenados. No estamos todav´ıa en condiciones de estudiar la ecuaci´on
de una par´abola cuyo eje de simetr´ıa no sea paralelo a ninguno de los ejes del sistema de
referencia que se considere.
Ejercicio. Expresa la ecuaci´on 2y2 + 4y + 3x + 7 = 0 en la forma
(y −

29. )2 = 2p (x − ).
Determina el v´ertice, el foco, la directriz y el eje de simetr´ıa de la par´abola y haz la repre-
sentaci´on gr´afica.
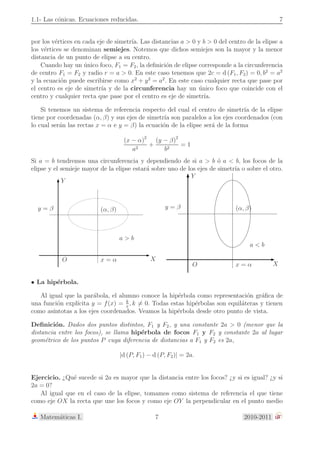
• La elipse.
Definici´on. Dados dos puntos F1 y F2 (iguales o distintos) y una constante 2a (mayor que
la distancia entre los focos), se llama elipse de focos F1 y F2 y constante 2a al lugar
geom´etrico de los puntos, P, cuya suma de distancias a F1 y F2 es 2a,
d (P, F1) + d (P, F2) = 2a.
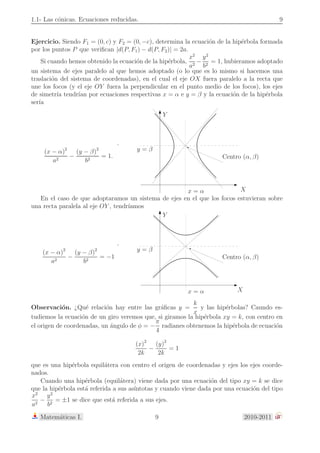
Ejercicio. ¿Qu´e sucede si 2a es igual a la distancia entre los focos? ¿y si es menor?
¿Qu´e sucede si F1 = F2?
Introducimos ahora un sistema de referencia respecto del cual la elipse estar´a caracteri-
zada por una ecuaci´on lo m´as simple posible. Tomamos como eje OX la recta que une los
focos F1 y F2 y como eje OY la recta perpendicular en el punto medio de los focos, punto
que ser´a por tanto el origen de coordenadas del sistema de referencia. Respecto de ´este de
referencia los focos vendr´an dados mediante F1 = (c, 0) y F2 = (−c, 0).
dejando una ra´ız cuadrada en cada uno de los miembros de la igualdad, È
Un punto P = (x, y) estar´a en la elipse si y s´olo si
d(P, F1) + d(P, F2) =
È
(x − c)2 + y2 +
È
(x + c)2 + y2 = 2a.
Sin m´as que hacer operaciones tenemos
(x − c)2 + y2 = 2a −
È
(x + c)2 + y2
elevando al cuadrado los dos miembros de la igualdad,
(x − c)2 + y2 =
2a −
È
(x + c)2 + y2
2
desarrollando,
È
(x + c)2 + y2
(x − c)2 + y2 = 4a2 + [(x + c)2 + y2] − 4a
È
(x + c)2 + y2
x2 + c2 − 2cx + y2 = 4a2 + x2 + c2 + 2cx + y2 − 4a
Matem´aticas I. 5 2010-2011

30. È
(x + c)2 + y2 = 4a2 + 4cx
6 Tema 1.- C´onicas y Cu´adricas.
simplificando y dejando en uno de los miembros de la igualdad s´olo la ra´ız cuadrada
4a
simplificando y elevando al cuadrado cada uno de los dos miembros de la igualdad,
a2
”
(x + c)2 + y2
—
=
€
a2 + cx
Š
2
,
desarrollando,
a2 [x2 + c2 + 2cx + y2] = a4 + c2x2 + 2a2cx
a2x2 + a2c2 + 2a2cx + a2y2 = a4 + c2x2 + 2a2cx,
simplificando, agrupando t´erminos y despejando,
(a2 − c2)x2 + a2y2 = a4 − a2c2 ⇔ (a2 − c2)x2 + a2y2 = a2(a2 − c2)
denotando b2 = a2 − c2( 0) y dividiendo ambos miembros de la igualdad por a2b2
tenemos
x2
a2 +
y2
b2 = 1, siendo b2 = a2 − c2.
x2
a2 +
X
y2
b2 = 1
Y
F2 = (−c, 0) F1 = (c, 0)
(a, 0)
(−a, 0)
(0, b)
(0,−b)
P = (x, y)
O
a
b
c
Es f´acil comprobar que el eje OX (la recta que une los focos) y el eje OY (la perpendicular
en el punto medio de los focos) son ejes de simetr´ıa de la elipse y su punto de corte (el
origen de coordenadas) es centro de simetr´ıa. Notemos que si un punto (x, y) verifica la
ecuaci´on de la elipse, los puntos
(±x,±y) : (x, y), (x,−y), (−x, y), (−x,−y)
tambi´en verifican dicha ecuaci´on. El eje de simetr´ıa que pasa por los focos suele denominarse
eje focal.
Los puntos en los que los ejes de simetr´ıa cortan a la elipse (±a, 0) y (0,±b) se denominan
v´ertices. Tambi´en suelen denominarse ejes de la elipse a los dos segmentos que se determinan
Matem´aticas I. 6Ingenier´ıas: Aeroespacial, Civil y Qu´ımica

31. 1.1- Las c´onicas. Ecuaciones reducidas. 7
por los v´ertices en cada eje de simetr´ıa. Las distancias a 0 y b 0 del centro de la elipse a
los v´ertices se denominan semiejes. Notemos que dichos semiejes son la mayor y la menor
distancia de un punto de elipse a su centro.
Cuando hay un ´unico foco, F1 = F2, la definici´on de elipse corresponde a la circunferencia
de centro F1 = F2 y radio r = a 0. En este caso tenemos que 2c = d (F1, F2) = 0, b2 = a2
y la ecuaci´on puede escribirse como x2 + y2 = a2. En este caso cualquier recta que pase por
el centro es eje de simetr´ıa y de la circunferencia hay un ´unico foco que coincide con el
centro y cualquier recta que pase por el centro es eje de simetr´ıa.
Si tenemos un sistema de referencia respecto del cual el centro de simetr´ıa de la elipse
tiene por coordenadas (,

32. ) y sus ejes de simetr´ıa son paralelos a los ejes coordenados (con
lo cual ser´an las rectas x = e y =

33. ) la ecuaci´on de la elipse ser´a de la forma
(x − )2
a2 +
(y −

34. )2
b2 = 1
Si a = b tendremos una circunferencia y dependiendo de si a b ´o a b, los focos de la
elipse y el semieje mayor de la elipse estar´a sobre uno de los ejes de simetr´ıa o sobre el otro.
a b
Y
(,

35. )
O X
x =
y =

36. (,

37. )
a b
Y
O X
x =
y =

38. • La hip´erbola.
Al igual que la par´abola, el alumno conoce la hip´erbola como representaci´on gr´afica de
una funci´on expl´ıcita y = f(x) = k
x , k6= 0. Todas estas hip´erbolas son equil´ateras y tienen
como as´ıntotas a los ejes coordenados. Veamos la hip´erbola desde otro punto de vista.
Definici´on. Dados dos puntos distintos, F1 y F2, y una constante 2a 0 (menor que la
distancia entre los focos), se llama hip´erbola de focos F1 y F2 y constante 2a al lugar
geom´etrico de los puntos P cuya diferencia de distancias a F1 y F2 es 2a,
|d (P, F1) − d (P, F2)| = 2a.
Ejercicio. ¿Qu´e sucede si 2a es mayor que la distancia entre los focos? ¿y si es igual? ¿y si
2a = 0?
Al igual que en el caso de la elipse, tomamos como sistema de referencia el que tiene
como eje OX la recta que une los focos y como eje OY la perpendicular en el punto medio
Matem´aticas I. 7 2010-2011