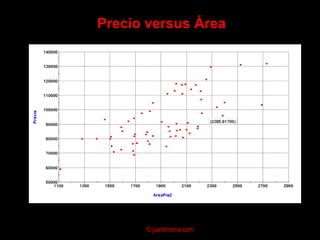
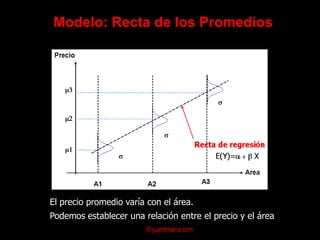
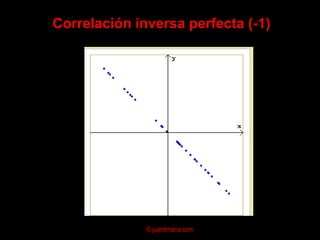
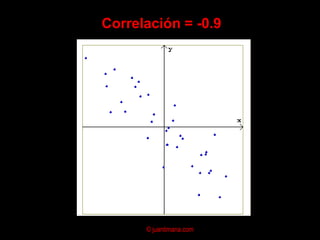
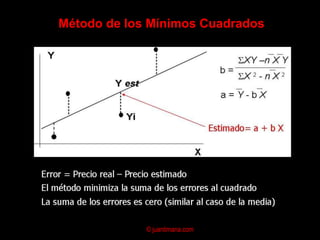
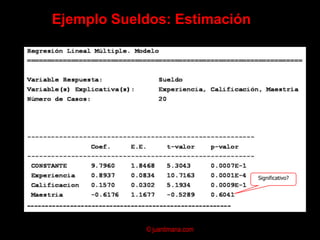
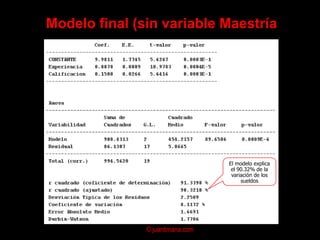
El documento presenta un análisis de regresión para estimar la relación entre el precio y el área de viviendas. Explica conceptos clave como la ecuación de regresión, el coeficiente de correlación, el método de mínimos cuadrados y supuestos del modelo de regresión lineal. Finalmente, analiza posibles problemas como la multicolinealidad y heterocedasticidad.

1. Análisis de RegresiónCaso Easton Realty

2. Precio versus Área

3. Precios con tres áreas diferentes

4. Modelo: Recta de los PromediosEl precio promedio varía con el área.Podemos establecer una relación entre el precio y el área

5. Análisis de Regresión¿Qué es el Problema de Regresión?Estimar el valor promedio de una variable en términos del valor conocido de otra variable (o valores conocidos de otras variables) ¿Qué es la Ecuación de regresión?Es la Expresión matemática que establece la relación entre dos variables¿Qué incluye el Análisis de Regresión?Estimar la fuerza de la asociación entre variablesDeterminar la relación apropiadaDeterminar el nivel de significancia de la relaciónEvaluar qué tan apropiada es la ecuación de regresión

6. Modelo desde otra perspectivaPara cada área hay un precio promedio pero también hay un conjunto de posibles valores alrededor de este promedio. Esta variación es producida por otros factores

7. Primer análisis: Diagramas de Dispersión

8. Coeficiente de Correlación de la muestraMide la asociación entre dos variables, indicando el sentido de la asociación.Tiene el mismo sentido ( es decir signo) que la pendiente del modeloPuede evaluarse su significancia

9. Correlación inversa perfecta (-1)

10. Correlación = -0.9

11. Correlación = -0.5

12. Correlación = 0.02

13. Correlación = 0.8

14. Correlación = 0.96

15. Nuestro caso: Precio vs Área

16. Modelo Lineal

17. Tres casos que hay que diferenciarEcuación del modelo para los promedios:E(Y) = A + B XEs la ecuación general, aplicable para los promediosEj. El precio promedio de una casa de 200m2Ecuación del modelo para valores individualesY = A + B X + error, Es aplicable para cada casaEj. El precio de una casa individual de 200m2Ecuación estimada Y = a + b XEs la ecuación estimada a través de una muestra de observaciones (lo que producen los datos)

18. Nuestra Recta: Precio vs Áreab= pendientea=intercepto

19. Método de los Mínimos Cuadrados

20. Valor estimado del precio YestEELa diferencia es el error eEEValor real del precioError Estándar del Estimador EE Desviación Típica de los Residuos

21. Coeficiente de Determinación (r2)Es el porcentaje de variación de Y explicada por el modeloIndica fuerza de asociación linealSe le usa como indicador de la capacidad predictiva del modelo Uso muy común pero no es lo único que debe considerarseExiste una versión mejorada llamado R2-ajustado

22. Supuestos del ModeloLa relación entre las variables es linealLas observaciones son independientesLa dispersión es constante en la rectaNormalidad: Cada distribución en cada valor de X es normal (necesaria para inferencia)

23. Inferencia en regresión¿Es la relación mostrada en la muestra generalizable a la población?

24. Prueba de hipótesis en la regresión

25. Pruebas acerca de la Pendiente

26. Resultado de una Regresión SimpleEcuación de regresión simpleEl precio se incrementa en 34.9 por pie2La pendiente es significativaLa variable área capacidad predictivaLa correlación es positiva igual que la pendienteError estándar del modelo de regresiónEl área explica el 48% de la variación del precio

27. Análisis de ResidualesResiduales versus valor estimadoNormalidad de los errores

28. Regresión MúltipleEn este caso tenemos más una variable independiente o explicativa

29. Regresión MúltipleEstudia la relación entre Una variable dependiente, yMás de una variable independiente (explicativa)Se utiliza:Para describir la naturaleza de una relaciónPara predecir la variables dependiente a partir del valor de las independientes

30. Detalles del modeloY = A + B X1 + C X2 + D X3 +…+ errorSe asume relación lineal Los términos A, B, C y los demás se interpretan como contribuciones marginales a la variación de YUna herramienta útil es la matriz de correlacionesIdealmente X1, X2, X3 y las demás variables explicativas son independientes entre síProblema potencial es la multicolinealidad

31. Ejemplo: Sueldos de graduados

32. Preguntas¿Cuál es el impacto de tener una maestría en el sueldo del ejecutivo?¿Qué variables son explicativas de las diferencias en el sueldo?Ofrezca una explicación razonable para el resultado hallado

33. Sueldos: Matriz de correlaciónObservar que Maestría no es una variable cuantitativaLa interpretación de la correlación tiene dificultades

34. Gráfica: Sueldos Vs. Experiencia

35. Gráfica: Sueldos Vs. Calificación

36. Gráfica: Sueldos Vs. Maestría

37. Ejemplo Sueldos: EstimaciónSignificativo?

38. Otros indicadoresMulticolinealidad?