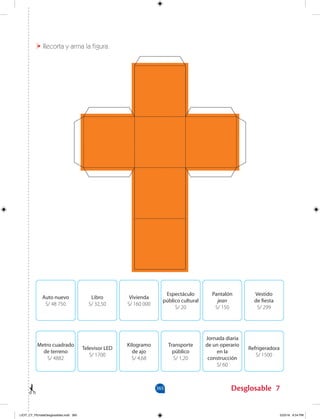
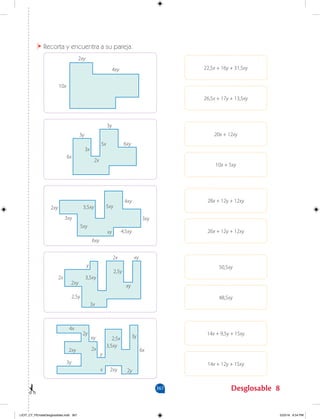
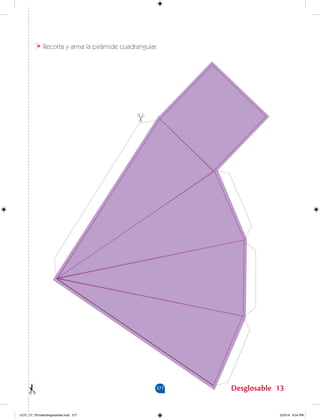
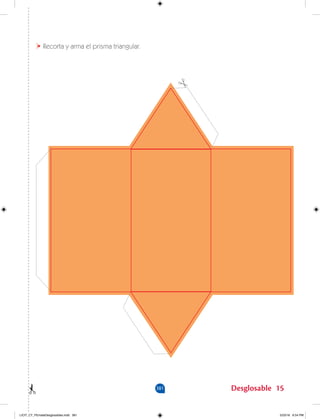
Este documento presenta un cuaderno de trabajo para matemáticas de secundaria. Explica que contiene actividades basadas en situaciones cotidianas para darle sentido práctico a los conceptos matemáticos. Además, describe las competencias matemáticas que se desarrollarán y los objetivos de aprendizaje de cada unidad.






















































































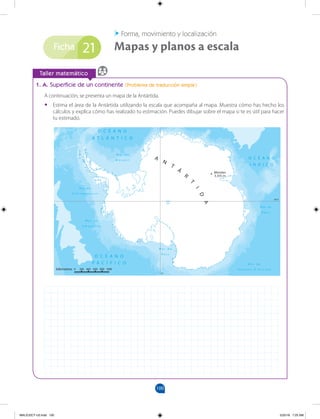












































![153
Metacognición
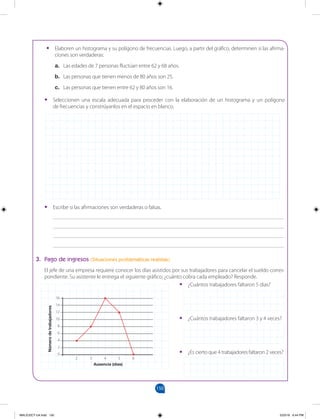
1. ¿Es importante en mi vida cotidiana organizar información en tablas de frecuencias y en gráficos
estadísticos?
Autoevaluación
Indicadores Siempre A veces Pocas veces
Relaciono cantidades y magnitudes en situaciones, y los expreso
en un modelo de aumentos y descuentos porcentuales sucesivos.
Empleo estrategias heurísticas, recursos gráficos y otros, para resolver
problemas relacionados con el aumento o descuento porcentual sucesivos.
Hallo el valor de aumentos o descuentos porcentuales sucesivos
al resolver problemas.
Justifico los procedimientos empleados para obtener un aumento
o descuento porcentual sucesivo.
Explico el significado del IGV y cómo se calcula.
Uso cuadros, tablas y gráficos estadísticos para mostrar datos
no agrupados y datos agrupados, y sus relaciones.
Organizo datos en histogramas y polígonos de frecuencias al resolver
problemas.
Justifico los procedimientos del trabajo estadístico realizado y la
determinación de la(s) decisión(es) para datos no agrupados y agrupados.
Coevaluación
Indicadores Siempre A veces Pocas veces
Tomamos una actitud crítica y reflexiva frente a situaciones problemáticas reales.
Respetamos las opiniones vertidas en torno a una situación problemática
planteada que requiere de la emisión de conclusiones.
Valoramos la importancia de aprender Matemática porque nos ayuda a
resolver situaciones reales.
Intervalos notas fi fr %
[13,5; 14,8[
[14,8; 16,1[
[16,1; 17,4[
[17,4; 18,7[
[18,7; 20]
n
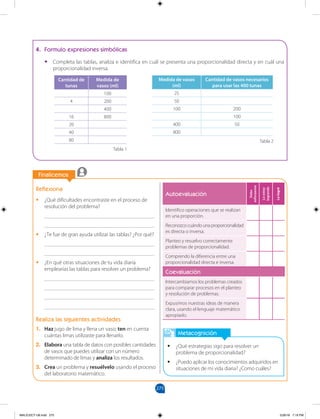
7. Elabora en una cartulina un plan de ahorro familiar para educación, con recomendaciones para una buena
práctica de ahorro.
Producto
MALICI2CT-U4.indd 153 5/23/16 6:44 PM](https://image.slidesharecdn.com/2matemtica-normapiscobamba-221220143720-1e442ca5/85/2-Matematica-Norma-piscobamba-pdf-153-320.jpg)




































































































































































![351
351
Sitios web
•
• AulaFacil. (2015). Curso gratis de estadística y pro-
babilidades. Recuperado de http://www.aulafacil.
com/cursos/t675/ciencia/estadisticas/estadisticas
•
• Centro Internacional de la Papa (CIP). (2006).
Catálogo de variedades de papa nativa. Recu-
perado de http://cipotato.org/wp-content/
uploads/2014/08/003524.pdf
•
• Chávez, D., Sabin, Y., Toledo, V. y Jiménez, Y. (2013).
La matemática, una herramienta aplicable en la in-
geniería agrícola. Recuperado de http://scielo.sld.
cu/pdf/rcta/v22n3/rcta14313.pdf
•
• Chumpitazi, M. (2012). La historia de la papa. [Info-
grafía]. Recuperado de https://infografiasos.files.
wordpress.com/2012/06/papa.jpg
•
• Coto, C. (s. f.). Introducciónalconocimientocientífico
experimental. Cap. 11. Recuperado de http://www.
quimicaviva.qb.fcen.uba.ar/contratapa/apren-
diendo/capitulo11.htm
•
• Definición.De. (2008). Definición de distancia. Recu-
perado de http://definicion.de/distancia/
•
• Dibujotecni.com. (2013). Dibujo técnico: Hexae-
dro. Recuperado de http://dibujotecni.com/siste-
ma-diedrico/hexaedro/
•
• Disfruta las matemáticas. (2011). Números decima-
les. Recuperado de http://www.disfrutalasmate-
maticas.com/numeros/decimales-menu.html
•
• Disfruta las Matemáticas. (2011). Transformaciones.
Recuperado de http://www.disfrutalasmatemati-
cas.com/geometria/transformaciones.html
•
• Edilatex. (2009). El plano cartesiano. Recuperado
de http://www.edilatex.com/index_archivos/alge-
bra5tintas.pdf
•
• Educar. (s. f.). Polígonos regulares. Recuperado de
http://www.educ.ar/sitios/educar/recursos/ver?i-
d=14925&referente=docentes
•
• Fundación Polar. (2006). Matemática para todos.
Recuperado de http://www.cienciaenlaescuela.
acfiman.org/matematica/fasciculo4/049.html
•
• Gaussianos. (2007). Construcciones con regla y
compás. Recuperado de http://gaussianos.com/
construcciones-con-regla-y-compas-iii-los-poligo-
nos-regulares/
•
• Hernández, R. (2004). Los elementos heurísticos en
la enseñanza de la matemática. Universidad de Ma-
tanzas. Recuperado de http://monografias.umcc.
cu/monos/2004/Informatica/um04II02.pdf
•
• Huapaya, E. (2012). Laetnomatemática:Perspectivas
pedagógicas y de investigación. [Ponencia del
III Encuentro de estudiantes de matemática y Fí-
sica. IPNM (2012)]. Recuperado de http://es.slides-
hare.net/enriquehuapaya1/iii-encuentro-de-estu-
diantes-de-matematica-fisica
•
• Instituto Nacional de Tecnologías Educativas y de
Formación del Profesorado. (2008). Conecto con las
mates. Recuperado de http://ntic.educacion.es/
w3//eos/MaterialesEducativos/primaria/matema-
ticas/conmates/actividades/jcloze49.htmy
•
• La Escuela Digital. (s. f.) Fracciones decimales. Recu-
perado de http://www.escueladigital.com.uy/arit-
metica/decimales.htm
•
• Lyczak, A. (2004). Probabilidad. [Recurso en línea].
Recuperado de http://www.thatquiz.org/es-d/ma-
tematicas/probabilidad/
•
• Matex Webside. (2006). Números fraccionarios.
¿Qué son los números fraccionarios? Recuperado
de http://docente.ucol.mx/grios/aritmetica/Num-
Fraccionarios.htm
•
• Micelli, M. y Crespo, C. (2011). La geometría entre-
tejida. Revista Latinoamericana de Etnomatemática.
Vol. 4. Recuperado de http://www.etnomatema-
tica.org/v4-n1-febrero2011/Micelli-crespo.pdf
•
• Ministerio de Educación. (2015). Rutas del apren-
dizaje. Recuperado de http://recursos.perueduca.
pe/rutas/documentos/Secundaria/Matemati-
ca-VI.pdf
•
• Ministerio del Ambiente. (2013). Como será un
mundo 4 °C más caliente. Recuperado de http://
www.minam.gob.pe/cambioclimatico/wp-con-
tent/uploads/sites/11/2013/10/images-17.pdf
•
• Museo de Historia Nacional. UNMSM. (2005). Ri-
queza mineral del Perú. Recuperado de http://mu-
seohn.unmsm.edu.pe/index.php/div/geo/dep-
minpet/86-museohn/geociencias/depminpet/
minpetroriqmin/81-minpetroriqmin
LICIT_CT_PEmate_bibliografia.indd 351 5/23/16 6:54 PM](https://image.slidesharecdn.com/2matemtica-normapiscobamba-221220143720-1e442ca5/85/2-Matematica-Norma-piscobamba-pdf-351-320.jpg)