El documento presenta información sobre las inferencias en la comprensión lectora. Explica que la inferencia es la operación cognitiva que permite obtener conclusiones a partir de premisas. Identifica diferentes tipos de inferencias como la holística, de datos, causal, prospectiva e intencional. Además, incluye ejercicios de comprensión lectora con diferentes textos y preguntas para practicar el uso de inferencias.

1. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 1
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS
Universidad del Perú, DECANA DE AMÉRICA
CENTRO PREUNIVERSITARIO
Habilidad Verbal
SEMANA 8 A
LAS INFERENCIAS EN LA COMPRENSIÓN LECTORA
En términos generales, la inferencia es la operación cognitiva que consiste en
obtener una conclusión determinada a partir de un conjunto de premisas. En la
comprensión lectora se trata de usar la inferencia para aprehender las relaciones
profundas de un texto, las ideas que no pueden entenderse gracias a una lectura
horizontal o superficial. Algunas modalidades son:
Inferencia holística: Es un tipo de inferencia por la cual el lector obtiene el marco
general que gobierna el texto sobre la base de los datos presentados en él.
Inferencia de datos: Es un tipo de inferencia por la cual el lector obtiene un dato
oculto en el texto, pero que se puede obtener sobre la base de otros datos explícitos en el
texto.
Inferencia causal: Es un tipo de inferencia por la cual el lector establece la causa
probable de un acontecimiento o fenómeno que se describe en el texto.
Inferencia prospectiva: Es un tipo de inferencia por la cual el lector obtiene un dato
futuro a partir de la información proporcionada en la lectura.
Inferencia de la intención: Es un tipo de inferencia por la cual el lector establece la
intención del autor sobre la base de algunas claves presentes en el texto.
EJERCICIOS DE INFERENCIAS EN COMPRENSIÓN LECTORA
TEXTO A
Aunque han transcurrido casi 32 años desde que China y el capitalismo iniciaran su
coqueteo, hoy un romance, una población de la nación oriental guarda fidelidad a Mao
Tse Tung. Tras un breve experimento con la «descolectivización», los habitantes de
Nanjie decidieron retomar los ideales del maoísmo y volver a la vida comunal, a las
libretas de racionamiento, y a adornar cada apartamento de la entidad con figurillas de
Mao. Esto ha convertido a Nanjie en un popular destino turístico retro, donde los visitantes
chinos llegan a admirar escenas como la marcha de la Milicia del Pueblo. No obstante, la
devoción maoísta de Nanjie enfrenta una dura prueba. Los funcionarios locales tratan de
desarrollar un parque comercial para atraer inversionistas extranjeros, así que han tenido
que desplazar a más de 100 residentes, y han provocado la indignación de los 3100
habitantes de Nanjie.
1. Se deduce del texto que Mao Tse Tung, durante la China comunista,
A) concilió con la visión capitalista.
B) obligó a su pueblo a adorarlo.
C) desplazó a funcionarios locales.
D) fue reverenciado solemnemente.*
E) instauró un gobierno despótico.

2. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 2
Solución:
Los habitantes de Nanjie han retomado viejos ideales. De esta forma las figurillas de
barro con la figura de Mao han vuelto a «adornar cada departamento». Se deduce
del texto que, en la época comunista de China, Mao era reverenciado por los
pobladores.
Clave: D
TEXTO B
Existen especies que requieren a los machos, pero no precisamente para lo que la
mayoría de las hembras de otras especies los requerirían. Tal es el caso de las molly
amazónicas. Estos diminutos peces de México y el suroeste de Estados Unidos son
ginogenéticos, es decir, clones femeninos naturales que necesitan aparease con machos
de una o dos especies estrechamente emparentadas con estos, cuyo esperma precipita el
desarrollo embrionario. El ADN del macho no se expresa: las crías son una copia al
carbón de la madre. El esperma sólo sirve para iniciar el proceso. Entonces, ¿qué ganan
estos machos si no pueden transmitir sus genes? Resulta que el apareamiento con las
molly les hace parecer más adecuados para la paternidad, desde el punto de vista de las
hembras de la especie a la que pertenecen.
1. Se colige del texto las molly amazónicas
A) no pueden trasladar sus genes.
B) liberan el esperma azarosamente.
C) carecen de especímenes machos.*
D) buscan los machos ginogenéticos.
E) expresan su ADN sólo en machos.
Solución:
Si las molly son clones de la madre, y requieren el esperma de otras especies, se
deduce que no existen especímenes machos.
Clave: C
TEXTO C
Centenares de copias del Corán, junto con otros antiguos manuscritos, se han
empolvado y deteriorado en los archivos de Al Azhar, el centro de estudios islámicos más
antiguo del mundo. Fundado en 972, en El Cairo, Al Azhar responde al desafío del tiempo
con la estrategia más moderna: digitalizar sus más de 128 mil volúmenes para publicarlos
en internet. La tarea es nada sencilla o barata. Sin embargo, gracias a una subvención del
jeque Mohammed bin Rashid al Maktoum, príncipe heredero del trono de Dubai, Al Azhar
ha contratado más de 100 empleados, 20 de los cuales operan una flotilla de escáneres
para generar una copia digital de cada página de la colección. No obstante, aunque las
imágenes computarizadas de un Corán del siglo XIII captan todo el contenido y la belleza
artística del libro, la grandiosidad de la obra solo puede apreciarse en el objeto mismo,
como ocurriría con una catedral medieval. Los colosales tomos dan fe de la talla del islam
antes de la invasión mongólica del siglo XIII, señala Akbar Ahmed, profesor de estudios
islámicos: «Son la extraordinaria expresión de una civilización en su apogeo».

3. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 3
1. Respecto del Corán original, se colige del texto que
A) su reconstrucción será total gracias a las versiones digitalizadas.
B) la invasión mongólica arrasó con todos los ejemplares del s. XIII.
C) su grandiosidad es superada por las catedrales de la Edad Media.
D) su destrucción a causa del polvo es inexorable a pesar del escaneo.
E) muchos de sus detalles serían inapreciables en la versión virtual.*
Solución:
En efecto, el texto indica que, aun cuando la versión virtual capta el contenido y la
belleza del Corán, la grandiosidad de la obras solo puede apreciarse en el objeto
mismo.
Clave: E
TEXTO D
En unos meses, los pingüinos de Magallanes del Zoológico de San Francisco
volverán a ser el centro de atención, para ver si repiten la representación que ofrecieran el
invierno pasado, de Navidad al Día de San Valentín. En aquella ocasión, los seis
ejemplares procedentes del parque Six Flags en Ohio, EUA, dirigieron a otros 46
pingüinos del zoológico en una maratón de natación alrededor del estanque. La razón
para tal explosión de actividad: en su nativa Suramérica, estos pingüinos migran dos
veces al año recorriendo tres mil kilómetros de costa en busca de alimento. Luego salen
del agua, ponen huevos, como hicieron las aves del zoológico. «La mudanza a California
se organizó para coincidir con la migración normal de los pingüinos», explicó Dee
Boersma, experta en pingüinos de Magallanes en la Universidad de Washington.
1. Se deduce del texto que la orquestada actividad de los pingüinos obedece al
A) cumplimiento natural de su reloj biológico.*
B) impulso de los administradores del zoológico.
C) papel de atracción que cumplen todos los años.
D) escaso espacio con que cuentan para desovar.
E) plan estratégico del zoológico para salvarlos.
Solución:
Los pingüinos fueron trasladados meticulosamente al zoológico de California en
cierta fecha para no desentonar con la migración anual que los pingüinos realizan
para desovar. Por esa razón, la intensa actividad evidenciada obedecía al
cumplimiento de su reloj biológico.
Clave: A
2. Es posible deducir del texto que los pingüinos
A) adquieren un instinto natural para bordear estanques.
B) suelen nadar distancias cortas para poder aparearse.
C) migran motivados por la escasez de comida y hábitat.
D) simulan la migración cuando se encuentran aislados.
E) siguen instintivamente el impulso de algún congénere.*
Solución:

4. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 4
Seis ejemplares de pingüinos dirigieron a otros 46, lo cual supone que, cuando un
pingüino hace algo, los demás lo siguen. Tal fue el caso evidenciado en el zoológico.
Clave: E
ELIMINACIÓN DE ORACIONES
1. I) Basil Berstein, preocupado por el proceso de socialización de los individuos,
prestó mucha atención al lugar que ocupa el lenguaje en este proceso. II) Esta
consideración de Berstein dio lugar a una teoría denominada la Teoría del déficit. III)
El déficit se define como la parte que falta para levantar las cargas del Estado,
reunidas todas las cantidades destinadas a cubrirlas. IV) La teoría del déficit
distingue dos formas de expresión lingüística, de uso de la lengua o de códigos: el
restringido y el elaborado. V) El código restringido predomina en la clase
trabajadora; el código elaborado, en las clases medias.
A) IV B) I C) III* D) V E) II
Solución:
Se elimina la III por impertinencia. El tema es la Teoría del déficit de Berstein.
Clave: C
2. I) Tutmosis III, después de la muerte de su madrastra Hatshepsut, prosiguió a
asegurarse su destino como uno de los más grandes faraones de la historia egipcia.
II) Tutmosis III fue un constructor de monumentos, pero también un guerrero sin par,
el llamado Napoleón del antiguo Egipto. III) Siempre que un estratega lleva a cabo
empresas bélicas impresionantes es comparado con Napoleón. IV) En 19 años
condujo 17 campañas en el Levante mediterráneo, incluyendo una victoria en contra
de los cananeos en Mégido, en el actual territorio de Israel. V) Durante la última
etapa de su vida, Tutmosis III afianzó su obra expansionista y decidió borrar
metódicamente de la historia a su madrastra Hatshepsut.
A) I B) II C) V D) IV E) III*
Solución:
Se elimina la III oración por impertinencia.
Clave: E
3. I) En un curso sobre gramática latina, Nietzsche sentencia que los conocimientos
más profundos están ya preparados en el lenguaje. II) Nietzsche se sirve de la figura
de Zaratustra para desarrollar y enlazar los elementos sobre los que se asienta su
obra. III) Nuestras más sofisticadas teorías acerca de la realidad están anticipadas
en los modos de decir y en el hecho de que tengamos que decir para saber y hacer
saber a otros. IV) No existe una distancia significativa entre el modo como tratamos
las cosas y el modo como las conocemos y nombramos, según Nietzsche. V) Este
es el punto de partida de una pragmática vitalista del lenguaje para Nietzsche.
A) II* B) III C) IV D) I E) V
Solución:
Se elimina la II por inatingencia. El tema desarrolla la apreciación de Nietzsche
acerca del lenguaje y la forma en que este contribuye a poner el mundo a
disposición del hombre.
Clave: A
4. I) Alexis II nació en Estonia en 1929 en una familia de nobles rusos emigrantes. II)

5. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 5
Alexis II presidió la Iglesia Ortodoxa Rusa desde el renacimiento de esta, en 1990,
hasta su muerte en diciembre de 2008. III) Su historia es la historia de la Iglesia y su
lucha contra el Estado. IV) Alexis sirvió como sacerdote y obispo durante 58 años
bajo el régimen soviético, que redujo a la Iglesia a un culto poco tolerado. V) Alexis
tomó como personal la misión de identificar a las víctimas de persecución comunista
que, a ojos de la Iglesia, murieron por su fe cristiana.
A) IV B) III C) II D) I* E) V
Solución:
Se elimina la I por impertinencia. El tema es la importancia de Alexis II en la
constitución de la Iglesia Ortodoxa Rusa.
Clave: D
5. I) Las azoteas de muchas edificaciones norteamericanas están conformadas por
jardines alternativos que cuentan con plantas que almacenan agua, y absorben la
lluvia que en un techo normal pasaría a filtrarse. II) La tierra natural se vuelve
excesivamente pesada al saturarse de agua en los techos, así que los arquitectos de
techos verdes utilizan tierra compuesta. III) El exceso de agua pluvial se filtra hacia
una capa de receptáculos o piedrecillas antes de derramarse hacia un drenaje; y, en
temporadas secas, las raíces absorben el agua acumulada. IV) La barrera de raíces
y una membrana impermeable aíslan el sistema de tejado vivo del edificio sobre el
que se desarrolla. V) La azotea verde de muchas edificaciones en EE. UU. está
compuesta por un conjunto de capas esenciales que cumplen funciones específicas
de absorción y drenaje.
A) III B) V* C) II D) IV E) I
Solución:
Se elimina la V por redundancia. Se encuentra implicada en las demás
Clave: B
SERIES VERBALES
1. Determine la alternativa que contenga un antónimo de FELONÍA.
A) Apología B) Ventura C) Moralidad D) Lealtad* E) Latrocinio
Solución:
El antónimo de felonía „traición‟ es deslealtad.
Clave: B
2. Bicicleta, biela; guardamonte, carabina; auto, capó;
A) fusil, bayoneta B) tocado, cofia C) clavija, carruaje*
D) cornete, cuerno E) cohetero, explosivo
Solución:
La serie verbal es de tipo mixto y está formada por pares que mantienen las
relaciones de TODO-PARTE, PARTE-TODO, TODO PARTE. La alternativa
adecuada que se ajusta a la relación PARTE-TODO es clavija, carruaje.
Clave: C
3. Determine la alternativa que contiene un hipónimo de cetáceo.

6. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 6
A) Laúd B) Róbalo C) Narval* D) Tiburón E) Manatí
Solución:
El término que se incluye por ser específico de cetáceo es narval „Cetáceo de unos
seis metros de largo, con cabeza grande, hocico obtuso, boca pequeña, sin más
dientes que dos incisivos superiores, uno corto y otro que se prolonga
horizontalmente hasta cerca de tres metros‟.
Clave: C
4. Lesivo, inocuo; obcecado, razonable; obsoleto, vigente;
A) obtuso, torpe B) lastimado, leso C) fúlgido, meridiano
D) fuliginoso, diáfano* E) letargoso, lento
Solución:
Serie analógica de antónimos.
Clave: D
5. Abjurar, apostatar; perpetrar, consumar; zaherir, humillar;
A) barruntar, conjeturar* B) transponer, circundar
C) proferir, enmudecer D) omitir, obturar
E) desvariar, razonar
Solución:
Serie verbal conformada por pares de sinónimos. El par de sinónimos que mantiene
consistentemente la relación es BARRUNTAR, CONJETURAR.
Clave: A
SEMANA 8 B
TEXTO 1
En Bulgaria, poco antes del 1000, apareció una secta que creía que el mundo y su
contenido material eran creación del Diablo. Para asegurarse la salvación, era necesario,
creían, abstenerse en lo posible de toda conexión con el mundo. La nueva secta
rechazaba el matrimonio, el sexo y el comer y beber más allá de lo estrictamente esencial.
La muerte era un bien categórico, y si todos los hombres muriesen y se librasen de sus
cuerpos materiales, tanto mejor. Esas creencias se difundieron por el Oeste y echaron
raíces en la Francia meridional. La actitud puritana ganó popularidad, como reacción, en
parte, contra la mundana corrupción de buena parte de los sacerdotes católicos, y la
herejía floreció. La ciudad de Albi, cerca de 360 kilómetros al sudoeste de Lyon, era un
centro fuerte de estos puritanos que se hacían llamar cátaros. En tiempos romanos había
sido la capital de una tribu gala cuyos miembros eran llamados los albigenses. De resultas
de esto, la secta fue llamada también de los albigenses.
La Iglesia aprobaba los sentimientos favorables a la pobreza y el puritanismo dentro
de ciertos límites, pero quería que fueran guiados por la jerarquía. No podía simpatizar
con el deseo de los cátaros de liberarse de la estructura administrativa eclesiástica. Los
cátaros no juzgaban necesario obedecer a los sacerdotes y los obispos contra los
dictados de su propia conciencia. La Iglesia podía fácilmente haber aplastado a esos

7. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 7
herejes, pero los cátaros hallaron simpatizantes entre muchos de los señores
meridionales. Estos señores quizá se hayan sentido atraídos por la doctrina, pero también
puede ser que viesen una oportunidad para expropiar tierras y riquezas eclesiásticas si
los herejes ganaban. El más fuerte defensor de los cátaros fue Raimundo VI, conde de
Tolosa. Pero en 1198 subió a la silla pontificia Inocencio III y, bajo su conducción, el
Papado medieval llegó al pináculo de su poder político. El prestigio del Papado se había
fortalecido mucho con el movimiento cruzado y ahora, bajo la dirección de un hombre
firme y resuelto, hasta podía someter a reyes fuertes. Inocencio era tal hombre. Envió un
legado a Raimundo para urgirlo a que tomase medidas para poner fin a la herejía, pero
Raimundo se negó a ello. Inocencio se hizo más firme en su insistencia y Raimundo en su
negativa, hasta que, en 1208, el legado fue muerto. Pronto circuló el cuento de que el
asesino había llevado a cabo su acción por orden de Raimundo, y el papa Inocencio, lleno
de ira, declaró la cruzada contra los herejes.
Muchos señores, ansiosos de obtener todos los beneficios religiosos que les
brindaría marchar a una cruzada, y de botín también, acudieron en masa a ofrecerse para
la tarea. El más eminente de ellos era Simón de Montfort, quien había combatido en
Tierra Santa contra los musulmanes y sabía exactamente cómo debía luchar un cruzado.
En 1209, los cruzados norteños tomaron la ciudad de Béziers, cerca de la costa
mediterránea. La ciudad fue saqueada, pero surgió la cuestión de saber cuáles de los
habitantes de la ciudad eran unos condenados herejes y cuáles eran buenos católicos.
Simón de Montfort (o quizá un legado del papa) halló una solución fácil. “Matadlos a todos
-dijo-, pues ya el Señor sabrá”. Así fueron muertos varias decenas de miles de hombres,
mujeres y niños.
La “Cruzada Albigense” dejó un mal legado en la forma de un temor a la herejía casi
paranoico por parte de muchos. Mientras los enemigos de la Iglesia fuesen judíos y
musulmanes, podían ser reconocidos fácilmente. Los herejes, en cambio, que creían en
Jesús y reverenciaban sus enseñanzas, habitualmente eran más difíciles de identificar.
Muy a menudo, sólo parecían cristianos excepcionalmente virtuosos (hasta el punto, de
hecho, de que la virtud misma daba pábulos a las sospechas de herejía). Si los herejes
hubiesen sido un peligro menor, podían ser combatidos localmente. Pero los cátaros
habían hecho necesaria una guerra antes de ser destruidos, por lo que se pusieron en
práctica métodos más drásticos para hacer frente a la herejía. Un organismo judicial
llamado la “Inquisición” fue creado en 1233. Examinaba las sospechas de herejía,
investigaba la cuestión (usando la tortura si era necesario, lo cual era un procedimiento
judicial común por la época) y luego, si la sospecha se confirmaba, se entregaba el hereje
a la autoridad secular para que le diese muerte. La Inquisición sirvió para suprimir las
disidencias de todo género, y en los distritos donde fue más activa, tuvo un mortal efecto
sobre la actividad intelectual y el fermento cultural. Donde tuvo más éxito en establecer la
unidad de opinión, lo hizo creando un desierto intelectual.
1. La expresión DAR PÁBULOS tiene el sentido preciso de
A) extinguir. B) revelar. C) cuestionar.
D) incentivar. * E) acusar.
Solución:
Los cristianos excepcionalmente virtuosos eran objeto de desconfianza pues su
virtud exagerada incentivaba la sospecha de que fueran herejes puritanos.
Clave: D
2. En el texto, el término PINÁCULO significa

8. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 8
A) término. B) cenit. * C) declive.
D) estancamiento. E) mínimo.
Solución:
El papado había ganado prestigio por las cruzadas y bajo la conducción de
Inocencio III incluso podía someter a reyes fuertes. El papado medieval estaba pues
en su apogeo, es decir, su momento de mayor poder.
Clave: B
3. En el primer párrafo, la expresión ACTITUD PURITANA implica
A) buscar con sumo empeño la muerte por inanición.
B) una tendencia a poblar profusamente este mundo.
C) el rechazo de la doctrina enseñada por Jesucristo.
D) la concepción del matrimonio como rito principal.
E) el escrupuloso cumplimiento de ciertos preceptos. *
Solución:
Mientras el clero era corrupto, los herejes cumplían escrupulosamente algunos
preceptos que predicaban por ejemplo la desconexión con el mundo material. De ahí
la fuerza del movimiento hereje.
Clave: E
4. El texto expone, fundamentalmente,
A) la creación de la Inquisición como instrumento de preservación de la fe.
B) el puritanismo consecuente de un movimiento herético medieval francés.
C) la cruenta represión de un movimiento herético en el medioevo francés. *
D) el acentuado carácter heterodoxo de una secta de la Francia meridional.
E) la refutación de una difundida herejía que mermaba el poder eclesiástico.
Solución:
El texto se centra en la sangrienta represión, fomentada por la iglesia católica, de
que fueron objeto los cátaros o albigenses del sur de Francia a inicios del siglo XIII.
Clave: C
5. En la matanza de Béziers, es posible inferir que un cátaro estrictamente
consecuente con sus ideas
A) habría encontrado una forma de liberación. *
B) lucharía hasta el final por imponer su visión.
C) evitaría la confrontación bélica a toda costa.
D) habría tratado de asesinar al noble Montfort.
E) diría que el genocidio es una orden diabólica.
Solución:
Un precepto cátaro sostenía que la muerte era un bien categórico y que si las
personas muriesen y se librasen de sus cuerpos materiales tanto mejor.
Clave: A
6. Con respecto a los cátaros o albigenses, es incompatible sostener que

9. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 9
A) fueron los depositarios de una implacable intolerancia religiosa.
B) estaban amparados por algunos señores de la Francia austral.
C) mostraban obsecuencia frente a las autoridades eclesiásticas. *
D) rechazaban la autoría divina de la creación del mundo material.
E) fueron percibidos como una amenaza por el poder eclesiástico.
Solución:
Los albigenses no eran sumisos frente a la administración eclesiástica, es más,
querían prescindir de ella y guiarse por los dictados de su conciencia.
Clave: C
7. Con respecto a Inocencio III, resulta incompatible aseverar que
A) fue el gestor de una empresa guerrera con connotación religiosa.
B) capitalizó la muerte de su representante en beneficio de su causa.
C) fue un Papa decidido y poseedor de una gran capacidad política.
D) desde un primer momento mostró animadversión por Raimundo VI. *
E) dirigía una institución que ya había luchado en guerras religiosas.
Solución:
En un primer momento, Inocencio III exhorta a Raimundo VI a poner fin a la herejía.
El legado papal es asesinado e Inocencio inicia una acometida sangrienta contra el
movimiento herético.
Clave: D
8. Si Raimundo VI hubiera observado las exigencias papales,
A) los cátaros se habrían suicidado en masa.
B) habría extendido sus dominios por Francia.
C) el papa Inocencio III lo habría canonizado.
D) habría podido derrotar a Simón de Montfort.
E) la cruzada albigense no habría tenido lugar. *
Solución:
Raimundo VI pudo evitar la furia papal si hubiese cedido ante él y si el legado de
este no hubiera muerto. Sólo ulteriormente y como respuesta a una afrenta,
Inocencio promueve una cruzada brutal contra los herejes.
Clave: E
9. Si la Inquisición no se hubiera institucionalizado en Europa
A) los cátaros se habrían apoderado del aparato administrativo católico.
B) el desarrollo de las ciencias y las letras habría sido mucho más fluido. *
C) Montfort permanecería impune por el genocidio de Béziers de 1209.
D) las disidencias en materia de fe serían alentadas por la misma iglesia.
E) el ateísmo habría proliferado inmediatamente en todo ese continente.
Solución:
La Inquisición generó un vacío intelectual provocado por el temor paranoico a incurrir
en una herejía y sufrir el castigo correspondiente. Como consecuencia, allá donde
triunfó la Inquisición hubo un desierto intelectual.
Clave: B
10. La primacía de la actitud inquisitorial acarreó como consecuencia la implantación del

10. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 10
A) puritanismo. B) agnosticismo. C) oscurantismo.*
D) racionalismo. E) vitalismo.
Debido a la Inquisición se difuminó la actividad cognoscitiva.
TEXTO 2
Uno de los mitos existentes sobre la metáfora es que es propia únicamente de los
registros formales, de la escritura, y sobre todo de la poesía y de algunos géneros
narrativos. En una obra ya clásica, Lakoff y Johnson (1980) refutan esta creencia
tradicional. Apoyándose en centenares de ejemplos, estos autores demuestran de manera
convincente que la metáfora está al orden del día también en el lenguaje cotidiano y que
afirmar lo contrario carece de fundamento. A partir de este estudio, la metáfora adquiere
un rango especial dentro de la naciente lingüística cognitiva. No se contempla como una
mera figura retórica, ni tampoco como una anomalía lingüística; al contrario, se entiende
como un proceso cognitivo que impregna nuestro lenguaje y nuestro habitual
pensamiento. La conclusión a la que se llega es que la base de la metáfora radica en
nuestro sistema conceptual: constituye un mecanismo para comprender y expresar
situaciones complejas sirviéndose de conceptos más básicos y conocidos.
La metáfora es un fenómeno tan ubicuo y tan usual que muchas veces ni siquiera
nos damos cuenta de su presencia en nuestro propio discurso. Aunque la naturaleza
figurada quizá no sea obvia a simple vista, ciertos enunciados como «La inflación siempre
sube más de lo que dice el gobierno», «En las rebajas de enero, caerán los precios»,
«Las acciones están por los suelos», entre otros, se valen de un proceso metafórico de
uso cotidiano, en el que la CANTIDAD se concibe en términos de VERTICALIDAD. Debido a
su alto grado de convencionalidad, esta metáfora resulta prácticamente invisible para el
hablante medio, en el sentido de que se trata de un esquema que está tan integrado en
nuestro sistema conceptual que no reparamos en su existencia de forma consciente. Sin
embargo, su carácter metafórico se hace patente al advertir que entidades abstractas
como los precios, la inflación, etc., no suben ni bajan en realidad como lo hace un avión al
volar; es decir, no se desplazan físicamente en un eje vertical hacia arriba o hacia abajo,
pero le atribuimos esas propiedades a partir de un marco conceptual que nos permite
materializar metáforas como la presentada.
1. Medularmente, el texto aborda el tema de
A) las anomalías lingüísticas en el lenguaje cotidiano.
B) las entidades abstractas y su verticalidad ascendente.
C) el lenguaje cotidiano y los esquemas conceptuales.
D) el arte literario de crear haciendo uso de metáforas.
E) la metáfora y sus implicancias en la vida cotidiana.*
Solución:
El texto desarrolla el tema de las metáforas usadas verbalmente en la vida cotidiana.
Clave: E
2. La palabra UBICUO, en el texto, connota
A) cotidianidad en el uso de expresiones metafóricas.*
B) creatividad sin parangón de las metáforas literarias.
C) invisibilidad de las metáforas en la vida cotidiana.
D) abstracción conceptual en el ámbito de la literatura.
E) omnipresencia de la metáfora en el ámbito económico.

11. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 11
Solución:
La palabra UBICUO connota el carácter extendido del uso de metáforas en la vida
cotidiana.
Clave: A
3. ¿Cuál es la idea principal desarrollada en el texto?
A) La lingüística se ocupa del formalismo y la sutileza creativa de las metáforas.
B) Nuestro sistema conceptual sirve para entender y expresar muchas situaciones.
C) El mito más conocido sobre la metáfora es que esta es eminentemente formal.
D) Lakoff y Johnson aseguran que la metáfora es un tropo literario sin relevancia.
E) El devenir cotidiano está signado, de manera masiva, por el uso de la metáfora.*
Solución:
En efecto, la idea principal es que la metáfora trasciende el contexto literario y está
íntimamente involucrada en nuestro devenir cotidiano.
Clave: E
4. Resulta incompatible con el texto afirmar que la noción de VERTICALIDAD
A) permite concretizar entidades abstractas a través del lenguaje.
B) materializa expresiones como «La inflación siempre sube más».
C) solamente se manifiesta en expresiones altamente especializadas.*
D) es un esquema que se encuentra muy integrado como concepto.
E) es implícita y pasa desapercibida debido a que es muy común.
Solución:
Este concepto permite que nos expresemos a través de metáforas; a su vez, estas
son productivas en la vida cotidiana, de manera que no se restringe a ámbitos
especializados.
Clave: C
5. Se deduce del texto que la interacción comunicativa de los individuos
A) se reduce a expresiones que involucran la noción de VERTICALIDAD.
B) es posible gracias a la aprehensión de esquemas convencionales.*
C) está regulada por expresiones que carecen de sentido figurado.
D) únicamente comprende y expresa situaciones simples y básicas.
E) se apoya de manera muy periférica e insustancial en la metáfora.
Solución:
Los esquemas conceptuales son básicos. Además, estos permiten expresar y
comprender situaciones complejas que se manifiestan en la interacción diaria.
Clave: B
TEXTO 3
En la actualidad, cuando contemplamos retrospectivamente la Francia de los
primeros Capetos, la concebimos como “Francia”, pero tal sentimiento no existía entre la
gente de la época. Cada provincia tenía su propio dialecto, distintivo y diferente, a veces
hasta muy diferente; y para cada grupo provinciano, los hombres que hablaban otros
dialectos eran extranjeros que debían ser despreciados, temidos u odiados, o todo a la
vez. Sin embargo, estaba por producirse un cambio. El espíritu y el ánimo de la era de las

12. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 12
Cruzadas dio origen a un sentimiento nuevo, más nacional, entre la gente. Por diferentes
que las personas de una u otra provincia se sintieran, todos eran cristianos y todos
luchaban contra los distantes musulmanes.
La Primera Cruzada también dio origen a la primera gran creación literaria que tuvo
gran popularidad en todas las provincias, atrajo a todos como una herencia común y dio a
todos un orgullo común. Era el Cantar de Roldán, que recibió su forma final alrededor del
1100. Su trama aprovechaba el sentimiento antimusulmán que despertó en los franceses
la Primera Cruzada. Su base histórica era un incidente que había ocurrido más de tres
siglos antes, cuando un monarca al que los franceses consideraban el más grande de su
historia, Carlomagno, había luchado gloriosamente contra los musulmanes en España.
Durante esa campaña, la retaguardia de uno de los ejércitos de Carlomagno, bajo el
mando de Roldán, fue destrozada por vascos cristianos en los desfiladeros de los
Pirineos. Pero el poema no contiene nada del suceso real. Mientras que Carlomagno, en
realidad, sólo conquistó la franja de España que está inmediatamente al sur de los
Pirineos, es pintado en el poema como si hubiera conquistado toda España excepto una
ciudad. La retaguardia es descrita como si hubiera sido atacada por un gran ejército
musulmán, en vez de las guerrillas cristianas, y todo el cuadro está pintado con los
fantasiosos colores heroicos de la caballería medieval. Cada cristiano combate con mil
musulmanes, excepto Roldán, que combate con diez mil. Hasta la derrota final de Roldán
es tan gloriosa como una victoria.
Ningún francés pudo evitar sentirse orgulloso de ser francés, cualquiera que fuese
su provincia, cuando leía este poema épico, que no solo fue el primero, sino también el
más grande de su tipo en la literatura medieval. El Cantar de Roldán dio origen a una gran
literatura imitativa de “cantares de gesta” (o cantares de hazañas caballerescas), de los
cuales unos ochenta han sobrevivido hasta hoy. La mayoría son fantasías concernientes
a los caballeros legendarios de la corte de Carlomagno. Los cantares de gesta, en
general, junto con la Primera Cruzada, dieron el primer gran impulso al nacionalismo
francés.
1. El texto versa fundamentalmente sobre
A) el sentimiento antimusulmán que fue plasmado en el Cantar de Roldán.
B) las cruzadas como grandes emprendimientos de la cristiandad medieval.
C) el gran influjo que tuvo el Cantar de Roldán en la literatura de su tiempo.
D) la adquisición de conciencia nacional de los antiguos dominios Capetos. *
E) el profundo respeto que la figura de Carlomagno despertaba en Francia.
Solución:
El texto se encarga de mostrar el modo en el que los dominios de una dinastía
dieron origen a la posterior nación francesa gracias a la fobia que despertaban los
musulmanes.
Clave: D
2. Una afirmación incongruente con el texto sostendría que
A) la diversidad dialectal era un poderoso óbice para la unidad francesa.
B) la cristiandad vivía en plena armonía antes de la irrupción musulmana. *
C) el Cantar de Roldán hizo escuela en la producción literaria medioeval.
D) los cantares de gesta destacan como composiciones monotemáticas.
E) el Cantar de Roldán se funda en la deformación de un hecho histórico.
Solución:

13. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 13
El mismo ejército de Carlomagno sufrió los embates de una guerrilla vasca cristiana
durante su incursión por España.
Clave: B
3. Se desprende del texto que el Cantar de Roldán es una composición literaria de
carácter
A) hiperbólico. * B) bucólico. C) filosófico.
D) dramático. E) religioso.
Solución:
La exageración de las hazañas de que da cuenta el Cantar de Roldán nos permite
afirmar su naturaleza hiperbólica.
Clave: A
4. Se puede inferir que la denominación “Francia”, aplicada a los dominios de los
primeros Capetos,
A) tuvo acogida antes de las cruzadas.
B) era una denominación despectiva.
C) es un mero recurso metodológico. *
D) acrecentó la producción literaria.
E) anuncia la llegada de la revolución.
Solución:
En esa época no existía la nación francesa como tal, por tanto, utilizamos
retrospectivamente la palabra “Francia” comparando las tierras de los Capetos con
el actual estado moderno francés que está en la misma región.
Clave: C
5. Si la primigenia Francia de los Capetos no hubiese tenido que enfrentar la amenaza
musulmana,
A) el nacionalismo francés se habría fundado en la fobia a los vascos.
B) la antigua dinastía capeta se habría extinguido irremediablemente.
C) el legendario Roldán no habría llegado a saborear nunca la derrota.
D) el sentimiento nacionalista francés no habría calado tan fácilmente. *
E) Carlomagno se habría empeñado en destruir las guerrillas vascas.
Solución:
Hacia el final del texto se afirma que la Primera Cruzada para hacerle frente a los
musulmanes, junto a los cantares de gesta, dieron el primer gran impulso al
nacionalismo francés.
Clave: D

14. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 14
ELIMINACIÓN DE ORACIONES
1. I) Uno de los elementos distintivos de la condición del esclavo es su exclusión
permanente, desde que nace, del seno de la comunidad. II) La ideología esclavista
suele manifestarse de manera encubierta en empresas multinacionales. III) La
disponibilidad de su cuerpo, su trabajo y su descendencia de acuerdo con las
necesidades de su amo es otro de los rasgos que caracteriza al esclavo. IV) La
condición de servidumbre al modelo más idóneo para hacer impotente y deshonroso
al esclavo a través de las leyes signa la vida del esclavo. V) La condición humana es
reemplazada por la consideración de que el esclavo, como sujeto, es similar a un
animal doméstico.
A) III B) V C) II* D) IV E) I
Solución:
Se elimina la II por impertinencia. El tema se centra en los rasgos predominantes de
la condición de esclavo.
Clave: C
2. I) El término eugenismo fue forjado en 1883, a partir de las raíces griegas que
significan «buena raza». II) En ese año fue planteado por Francis Galton para
designar a la ciencia de las condiciones favorables para la reproducción humana. III)
La palabra eugenismo, desde su aparición en 1883, ha ostentado un carácter
evidentemente polisémico. IV) La palabra eugenismo suele emplearse también para
designar el movimiento sociopolítico, ideológico, que sostiene la práctica de la
eugenesia. V) A su vez, el eugenismo es un objeto histórico y un tema siempre
actual de cuestionamiento moral.
A) IV B) II C) V D) III* E) I
Solución:
Se elimina la III porque está incluida en las demás oraciones.
Clave: D
3. I) La concepción feminista combate el pensamiento occidental que denigre de forma
explícita a la mujer, tal y como se puede apreciar en Aristóteles, Kant, Rousseau,
entre otros II) El feminismo también estima que, en la mayoría de discusiones
filosóficas sobre la ética aplicada, las mujeres son tratadas como medios para
promover los intereses de los hombres. III) El carácter normativo de la experiencia
masculina, que excluye el papel de la mujer en la práctica filosófica y genera una
experiencia moral específicamente masculina, también es rechazada por la filosofía
feminista. IV) Asimismo, las feministas recusan la tradición occidental que, de
manera sostenida, devalúa lo femenino asociando el término más valorado a lo
masculino y el menos valorado a lo femenino. V) La posición feminista reprocha a
los filósofos occidentales sus diferentes formas de prejuicios desfavorables para las
mujeres.
A) V* B) I C) III D) II E) IV
Solución:
La V está incluida en las demás oraciones.
Clave: A

15. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 15
4. I) El egoísmo y el altruismo siempre constituyeron objetos de interrogación para la
filosofía. II) Platón es uno de los primeros en preguntarse si los seres humanos son
capaces de preocuparse por algo que no sea de su propio interés. III) De esta
manera, la República está consagrada al estudio de nuestra capacidad de sacrificar
nuestros intereses personales en nombre de la justicia. IV) La concepción platónica
de la justicia se interesa principalmente en la buena disposición del alma. V) No
obstante, para Platón, probablemente, el factor esencial de la motivación se vincula
con una consideración «egoísta» individual (se actúa con miras al buen estado de la
propia alma).
A) III B) I* C) II D) IV E) V
Solución:
Se elimina la oración I porque es impertinente.
Clave: B
5. I) Los manatíes son herbívoros, y se alimentan de unos 60 tipos diferentes de
plantas. II) La palabra de la lengua indígena caribeña manatí significa «con mamas».
III) Un manatí adulto puede comer normalmente hasta un 9% de su peso (unos 50
kg) al día. IV) Cada 2 a 5 años la hembra da a luz una cría, la cual al nacer en
promedio pesa 35 kg y mide de 90 a 120 cm de largo. V) Solamente la hembra se
encarga de cuidar la cría, dándole leche hasta que sus dientes están bien formados
para comer alimentos duros.
A) III B) IV C) I D) II* E) V
Solución:
Se elimina la II por impertinencia.
Clave: D
SEMANA 8 C
TEXTO 1
En Italia, desde el siglo XIV, los eruditos intentaban hacer revivir e interpretar de
nuevo el canon de las obras clásicas. Para ilustrar la dignitas hominis (la dignidad del
hombre) que, según ellos, era subestimada por los filósofos medievales, los humanistas
volvieron a acudir sobre todo a la filosofía moral de los antiguos, por ser una disciplina
basada en la razón y en el uso del sentido común; consideraban que las éticas paganas
debían demostrar ser útiles para los laicos que vivían bajo los preceptos la época.
Esta posición, asociada a una toma de conciencia cada vez más marcada sobre la
dignidad y el deber cívicos en la Italia del Renacimiento, fue también aceptada por
reformadores como Lutero y, en particular, Melanchthon, quienes mantenían
estrictamente por separado lo sagrado y lo profano. Los filósofos humanistas
denunciaron, tal vez injustamente, el apego maniático de sus predecesores a la lógica
abstracta y deformada del Aristóteles medieval y a su irreprochable pero inhumana
disección de cada tema.
Era en parte una cuestión de estilo: los humanistas estimaban que la toma de
conciencia personal acerca del tema moral podía ser más suscitada por un escritor
pagano elocuente que por las argucias impersonales de los teólogos de profesión. En
realidad, las obras de Aristóteles contribuyeron mucho al desarrollo de la filosofía moral

16. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 16
del Renacimiento, pero los humanistas se inspiraron en otras tres tradiciones antiguas
importantes para formar sus ideas éticas y elaborar los modelos de su elocuencia
inspirada: el idealismo platónico, el estoicismo y el epicureísmo. Lógicamente, la
explotación de estas fuentes «paganas» los llevaron a entrar en conflicto con los teólogos
de su época.
1. El tema central desarrollado en el texto es
A) el humanismo del Renacimiento.*
B) el paganismo de la Edad Media.
C) la doctrina moral de Aristóteles.
D) la reforma religiosa de Lutero.
E) el epicureísmo y el estoicismo.
Solución:
El texto desarrolla los aspectos más relevantes de la filosofía humanista del
Renacimiento, la cual devino en una fricción con los teólogos de su época.
Clave: A
2. En el texto, la palabra ESTIMAR adquiere el sentido de
A) calcular. B) valorar. C) apostar.
D) postular. E) considerar.*
Solución:
La palabra en cuestión adquiere el sentido de considerar.
Clave: E
3. Resulta incompatible con el desarrollo textual afirmar que
A) el tema moral era considerado como un atributo propio de los escritores paganos.
B) en el siglo XIV, algunos estudiosos escindían claramente lo pagano de lo profano.
C) los eruditos italianos promovían la interpretación del canon de las obras clásicas.
D) la concepción humanista de los filósofos renacentistas mostraba sesgo pagano.
E) la filosofía humanista del Renacimiento se circunscribió a la doctrina aristotélica.*
Solución:
La filosofía humanista se inspiró en tres fuentes: el idealismo platónico, el estoicismo
y el epicureísmo. En (E) se afirma que únicamente la doctrina aristotélica influyó en
dicha forma de pensar.
Clave: E
4. Se deduce, a partir de las premisas textuales, que las obras de Epicuro o las de
Zenón de Citio, fundador del estoicismo,
A) formaban parte de la práctica exegética de los teólogos.
B) rechazaban de manera extremista la dignitas hominis.
C) eran cuestionadas por los religiosos de la Edad Media.*
D) fueron cuestionadas por el reformador Martín Lutero.
E) eran tan abstrusas como la visión aristotélica medieval.

17. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 17
Solución:
En el texto se señala claramente que los filósofos humanistas se encargaron de
develar el mundo griego a partir de tres fuentes de rigor: el epicureísmo, el
estoicismo y el idealismo platónico; estas influencias «los llevaron a entrar en
conflicto con los teólogos de su época».
Clave: C
5. Si la tarea intelectual de los humanistas hubiese consistido únicamente en una
reinterpretación de los postulados aristotélicos, probablemente,
A) los teólogos medievales hubieran proscrito todo tema basado en la moral.
B) el Renacimiento no hubiese reflexionado acerca de la dignidad humana.*
C) sería injusto señalar que hubo un apego maniático a la lógica aristotélica.
D) tendríamos que replantear cronológicamente la aparición de la Edad Media.
E) los teólogos hubiesen pugnado acremente con los filósofos humanistas.
Solución:
La lectura de los postulados platónicos, estoicos y demás fueron el germen de la
filosofía humanista, la cual se planteó el tema de la dignidad humana. De no haber
centrado su atención en estas fuentes, probablemente este tema hubiese quedado
soslayado.
Clave: B
TEXTO 2
Aunque la herencia de los caracteres biológicos se ha reconocido hace miles de
años, la primera idea importante sobre el mecanismo implicado se dio hace casi 150
años. En 1866, Gregor Johann Mendel publicó los resultados de una serie de
experimentos que sentaron las bases de la genética como disciplina formal. Aunque el
trabajo de Mendel pasó largo tiempo inadvertido hasta 1900, después del
redescubrimiento del mismo, se estableció el concepto de gen como unidad hereditaria
discreta. Se clarificó el modo en que los genes, como miembros de los cromosomas, se
transmiten a los descendientes y controlan los caracteres. La investigación ha continuado
sin pausa durante el siglo XX. Realmente, los estudios en genética, y más recientemente
aquellos que se refieren al ámbito molecular, han permanecido en la frontera de la
investigación biológica desde principios del siglo XX.
Cuando Mendel comenzó sus estudios sobre la herencia utilizando Pisum sativum,
el guisante de jardín, no se sabía de la existencia de los cromosomas ni del papel y
mecanismo de la meiosis. No obstante, Mendel pudo determinar la existencia de unidades
de herencia discretas y predecir su comportamiento durante la formación de los gametos.
Investigadores posteriores, con acceso a datos citológicos, pudieron relacionar sus
observaciones sobre el comportamiento de los cromosomas en la meiosis con los
principios de la herencia de Mendel. Una vez que se estableció esta correlación, los
postulados de Mendel se aceptaron como la base para el estudio de lo que se conoce
como la genética mendeliana o de la transmisión. Estos principios describen de qué
manera se transmiten los genes de padres a hijos y derivan directamente de los
experimentos de Mendel. Incluso hoy día constituyen la piedra angular de los estudios
sobre la herencia.

18. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 18
1. La idea principal del texto sostiene que
A) los principios de la herencia de Mendel son producto de la experimentación.
B) la especie Pisum sativum fue crucial para los experimentos mendelianos.
C) el ADN constituye la unidad hereditaria discreta que controla los caracteres.
D) Mendel fue injustamente ignorado por la comunidad científica de su tiempo.
E) los estudios mendelianos constituyen el acta de nacimiento de la genética. *
Solución:
El texto se dedica a afirmar la importancia de Mendel para la genética de la
transmisión. Sus estudios sentaron las bases de la genética como disciplina formal.
Clave: E
2. La expresión PIEDRA ANGULAR tiene el sentido preciso de
A) finalidad. B) excepción. C) fundamento. *
D) obstáculo. E) corolario.
Solución:
Los principios de la herencia de Mendel son la base o fundamento principal de los
estudios en torno a la herencia a través de los genes.
Clave: C
3. Resulta incompatible con el texto afirmar que
A) Mendel comprendió que los caracteres están regidos por algún tipo de unidad
física.
B) La experiencia mendeliana fue pionera en las investigaciones en torno a la
herencia.
C) la meiosis es un proceso celular cuya comprensión no estaba al alcance de
Mendel.
D) la transmisión hereditaria era totalmente ignorada antes de los estudios de G. J.
Mendel. *
E) los notables estudios de Mendel fueron objeto de la indiferencia de sus
coetáneos.
Solución:
La transmisión de caracteres es un hecho reconocido desde hace miles de años.
Mendel hace inteligible el fenómeno a través de la exposición del mecanismo que lo
hace posible.
Clave: D
4. Es posible inferir que los modernos estudios citológicos
A) desconcertaron totalmente a los epígonos de Gregor Mendel.
B) son una consecuencia directa de la investigación mendeliana.
C) corroboraron los resultados de las investigaciones de Mendel. *
D) contradicen los resultados de los estudios con Pisum sativum.
E) descartaron de plano la posibilidad de existencia de la meiosis.
Solución:

19. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 19
El comportamiento de los cromosomas en la meiosis fue asociado a los principios de
la herencia de Mendel y con ello sus postulados se aceptaron como la base de la
genética de la transmisión.
Clave: C
5. Si los caracteres biológicos no se transmitieran de una generación a otra,
A) la investigación mendeliana habría sido considerada desde el inicio.
B) la genética habría surgido de todas maneras como disciplina formal.
C) Mendel habría tenido que experimentar con una especie diferente.
D) la biología misma habría perdido fundamento como ciencia natural.
E) el concepto de gen sería totalmente intrascendente para la ciencia. *
Solución:
Los estudios mendelianos parten precisamente de la necesidad de dar cuenta del
mecanismo de la herencia de los caracteres biológicos. Este mecanismo entraña la
existencia de los genes como unidades hereditarias.
Clave: E
TEXTO 3
La filosofía social de Marx se basaba y fue la primera en llamar la atención sobre un
cambio social de primerísima importancia que se produjo en el siglo XIX: el surgimiento de
la conciencia política y, finalmente, el ascenso hacia el poder político, de una clase
trabajadora industrial. Esto fue determinante para cambiar el curso del pensamiento
liberal, pero Marx percibió su importancia mucho antes que los liberales. Especialmente
en los estudios históricos que formaban parte integrante de su filosofía, presentaba al
capitalismo por primera vez en lo que podría llamarse su aspecto humano, como
institución que había producido y aumentaba constantemente una clase de hombres que
tiene que vivir absolutamente del salario y que se relacionaba, pues, con los patronos sólo
mediante un nexo monetario. Su fuerza de trabajo es una mercancía, la única mercancía
económicamente valiosa que poseen, que debe ser vendida en un mercado competitivo
donde la única obligación del comprador es pagar el precio establecido. La relación de
patrón y obrero en la industria tiende a quedar desprovista, así, de sentido humano y de
obligación moral y se convierte simplemente en una relación de poder. Marx vio
justamente en esta situación el hecho potencialmente más revolucionario de la historia
moderna; por una parte, una clase definida por su propiedad de los medios de producción
y motivada esencialmente por la necesidad de crear ganancias y, por otra parte, un
proletariado industrial sin ningún poder salvo a través de la presión de las masas
organizadas y obligado a fijarse como fin no la libertad política sino el sostenimiento o el
mejoramiento de su nivel de vida. Entendiendo esto como un hecho histórico, Marx
concebía al capitalismo como institución, no como resultado de leyes económicas
intemporales sino como fase en la evolución de la sociedad moderna. Partiendo, pues, del
hecho de los intereses divergentes de clases, ya bien aclarados por los economistas
clásicos, se dedicó a interpretar el liberalismo político como ideología característica de la
clase media y a crear una filosofía social para el proletariado en ascenso, apropiada para
servirlo en su lucha por el poder.
1. El texto trata fundamentalmente acerca de

20. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 20
A) el contraste entre los intereses de los patrones y los obreros.
B) la explotación que sufre el obrero en el seno del capitalismo.
C) las bases sobre las que descansa la filosofía social de Marx. *
D) el desarrollo de la historia desde el punto de vista marxista.
E) la urgencia de la organización política de la clase trabajadora.
Solución:
En el texto se observa que la filosofía social de Marx se sustenta en el surgimiento
de la conciencia política del proletariado y de su posterior lucha por el poder.
Clave: C
2. Marx fundamentó su filosofía social sobre la base del descubrimiento de
A) la circularidad de la historia.
B) odio entre patrones y obreros.
C) un arraigado nacionalismo.
D) la ideología de la clase media.
E) una contradicción de clases. *
Solución:
Marx descubre dos clases sociales antagónicas; una que es dueña de los medios de
producción y otra que solamente posee su fuerza de trabajo.
Clave: E
3. Una afirmación incompatible con lo vertido en el texto aseveraría que
A) la visión marxista de la historia tiene naturaleza dinámica.
B) el capitalismo ha engendrado a la clase social trabajadora.
C) Marx dedicó parte de su esfuerzo al estudio de la historia.
D) el liberalismo es la ideología de la más alta aristocracia. *
E) el marxismo y el liberalismo constituyen ideologías disímiles.
Solución:
En el texto se afirma que la única posesión del proletariado es su fuerza de trabajo,
la cual vende en un mercado altamente competitivo.
Clave: D
4. Se desprende del texto que la fuerza del proletariado radica en
A) su infinita fuerza para el trabajo.
B) poseer los medios de producción.
C) la firmeza de sus valores morales.
D) el tesón para lograr sus objetivos.
E) su adecuada organización política. *
Solución:
El texto sostiene que el proletariado, en contraposición con los dueños de los medios
de producción, no tiene ningún poder, excepto la presión de las masas organizadas.
Clave: E

21. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 21
5. Si la equidad hubiese sido la marca distintiva de la relación entre patrones y
proletarios,
A) serían estos últimos quienes terminen explotando a los patrones.
B) Marx no habría concebido una visión antagónica de la historia. *
C) el pensamiento marxista centraría su atención en la gnoseología.
D) la filosofía social de Marx reivindicaría a una tercera clase social.
E) el capitalismo habría logrado sobrevivir al desarrollo de la historia.
Solución:
Fue precisamente la desigualdad de las condiciones de ambas clases sociales la
que indujo a Marx a pensar que estaba frente a el hecho potencialmente más
revolucionario de la historia moderna.
Clave: B
SERIES VERBALES
1. Pietista, asceta; dadivoso, mezquino; estulto, necio;
A) imparcial, ecuánime B) aprensivo, flatoso C) flexuoso, ondulado
D) temerario, prudente* E) gitanesco, flamenco
Solución:
La serie verbal está formada por una secuencia de SINÓNIMOS, ANTÓNIMOS,
SINÓNIMOS. Corresponde el par de antónimos temerario „demasiado atrevido‟ y
prudente „cauteloso‟.
Clave: D
2. Agraciado, bonito, lindo,
A) hercúleo B) bellido* C) galante D) esbelto E) airoso
Solución:
La serie se completa con un sinónimo de bonito, lindo; a saber, bellido.
Clave: B
3. Enojo, enfado, ira,
A) maraña B) intriga C) cólera* D) frenesí E) letargo
Solución:
La serie se completa con un sinónimo de enfado, cólera; a saber, mohína.
Clave: C
4. Laudable, encomiable; lascivo, lujurioso; nulo,…
A) latoso B) írrito* C) risible D) infundado E) irredento
Solución:
La serie está formada por SINÓNIMOS; de esta forma, el único sinónimo de nulo es
írrito.
Clave: B

22. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 22
5. Fatigado, cansado, agotado,
A) irritado B) apacible C) pusilánime
D) exhausto* E) vigoroso
Solución:
El sinónimo que completa la serie verbal es transido „fatigado, acongojado‟.
Clave: D
6. Determine la palabra que no se ajusta a la relación semántica de las demás.
A) Gaje B) Estipendio C) Jornal D) Emolumento E) Óbolo*
Solución:
Serie verbal formada por cohipónimos de REMUNERACIÓN. La palabra óbolo es
cantidad de dinero que se otorga voluntariamente para un determinado fin, es una
contribución no un pago o remuneración.
Clave: E
ELIMINACIÓN DE ORACIONES
1. I) Según Ramón Trujillo, el significado es una intuición idiomática, y en tanto
intuición, es imposible que se lo pueda definir. II) Lo que se define en los
diccionarios, según este semantista español son los sentidos de las palabras. III) Los
sentidos son para Trujillo las relaciones que los significados sostienen con referentes
de la realidad. IV) El sentido y el significado son nociones que se confunden y se
toman por equivalentes. V) Los referentes no son objetos lingüísticos, razón por la
cual las definiciones no pueden ser construcciones objetivas del significado, enfatiza
Trujillo.
A) IV* B) II C) V D) I E) III
Solución:
Se elimina la IV, ya que está implicada en las demás.
Clave: A
2. I) Émile Durkheim es conocido como el gran maestro de la sociología francesa y fue
con el nombre de este intelectual que la sociología alcanzó estatus de autonomía en
la universidad francesa. II) La división del trabajo, obra de Durkheim, desarrolla el
tema de las reglas sociales, cuyo papel es el mismo que desempeña la «ley» en
Kant. III) La división del trabajo está constituida sobre un esquema dinámico que
lleva del individuo-organismo al individuo-persona. IV) En esta obra, Durkheim
tomaba ya una posición ambigua respecto del derroche moral en todos los dominios,
salvo en lo que concierne al valor del individuo. V) En La división del trabajo,
Durkheim plantea que el individuo es el punto de reunión de las aspiraciones
colectivas, además de desarrollar sus intereses propios.
A) II B) V C) III D) IV E) I*
Solución:
Se elimina la I por impertinencia. Las demás oraciones abordan la obra de Durkheim
La división del trabajo.
Clave: E

23. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 23
Aritmética
EJERCICIOS DE CLASE Nº 8
1. Sea una fracción equivalente a
447
1192
tal que sus términos sean los menores
posibles. Si la suma de sus términos es
o
9 y la diferencia de sus términos es
o
55 , halle la suma de cifras del denominador.
A) 18 B) 9 C) 21 D) 22 E) 36
Solucion:
o
o
3k
f =
8k
11k = 9
5k = 55
8k = 792
k = 99
Clave: A.
2. La expresión
3K +13
2K - 3
representa un número entero positivo, ¿cuántos valores
enteros puede tomar K?
A) 6 B) 5 C) 4 D) 3 E) 2
Solucion:
3 13 1 35
3
2 3 2 2 3
k
k k
  
    
R =  R  Z 2k – 3 es divisor de 35
K toma 5 valores
Clave: B.
3. Sea
a
b
el menor número irracional irreductible mayor que
5
12
tal que al sumar
“n” veces el denominador al numerador y “n” veces el numerador al
denominador se obtiene el número 2. Halle el valor de: a + b
A) 14 B) 25 C) 27 D) 10 E) 24
Solucion:
2
2 5
2 1 12
a nb
b an
a n
b n




 


10
8
19
27
n
a
b
a b


 
Clave: C.
4. Si las siguientes fracciones:
19 20 21 91
; ; ;...;
K +21 K +22 K +23 K +93
son irreductibles, halle el menor valor de “K”
A) 89 B) 91 C) 94 D) 95 E) 97

24. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 24
Solucion:
Si k + 21  19 (pesi)  k + 2  19 (pesi)
k + 2  20 (pesi)
k + 2  21 (pesi)
. .
. .  k = 95
. .
k + 2  91 (pesi)
k + 2  97 (pesi)
Clave: D.
5. ¿Cuántas fracciones equivalentes a
68
119
existen que sean de la forma
ab
ba
?
A) 3 B) 5 C) 6 D) 7 E) 4
Solucion:
4
7
k
f
k
  k= 3; 6; 9; 12
Clave: E.
6. ¿Cuántas fracciones comprendidas entre
19
43
y
23
29
son tales que sus términos
son números consecutivos?
A) 3 B) 2 C) 1 D) 4 E) 5
Solucion:
19 23
43 1 29
n
n
 

 n = 1, 2, 3
0,4…< n <3,8…
Clave: A.
7. Un alambre se dilata en un proceso de manufactura:
1
3
de su longitud la
primera vez;
1
4
de su nueva longitud la segunda vez;
1
5
de su nueva longitud
la tercera vez y así sucesivamente. Después de 20 procesos mide 690 metros
¿Cuál fue la longitud inicial?
A) 88m B) 90m C) 89m D) 91m E) 92m
Solucion:
Longitud inicial = L
23 22 21 6 5 4
. . ... . .
22 21 20 5 4 3
L = 690
L = 90 m
Clave: B.

25. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 25
8. Si
64
K
es una fracción propia e irreductible mayor que
4
15
. ¿Cuántos valores
puede tomar “K”?
A) 97 B) 79 C) 88 D) 83 E) 93
Solucion:
4 64
1
15 k
 
64 < k < 240
K = 65; 67; 69; …;239
 k = 88
Clave: C.
9. ¿Cuál es la menor cantidad entera que debe agregarse a los términos de la
fracción
4
7
para que la fracción resultante este comprendida entre 0,7 y 0, 75?
A) 1 B) 2 C) 3 D) 4 E) 5
Solucion:
7 4 3
10 7 4
k
k

 

 k = 4
Clave: D.
10. Si K  Z tal que
2
7K -5K
K +1
 Z.
Halle la suma de todos los valores de K
A) 12 B) – 11 C) 11 D) 10 E) – 12
Solucion:
2
7 5 12
7 12
1 1
k k
k
k k

  
 
  valores de k = - 12

12
1k 
 Z
Clave: E.
11. Determine cuántas fracciones propias e irreductibles de numerador 110 existen
tales que sean mayores que
23
37
.
A) 24 B) 20 C) 14 D) 25 E) 23
Solucion:
23 110
1
37 D
  pero D  110 (PESI)
111 < D < 176 D  2
o
; 5
o
; 11
o
Existen 24 valores Clave: A.

26. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 26
12. Si de un tonel lleno de vino; se extraen
2
5
de lo que no se extrae y se llena de
agua. Si esta operación se realiza tres veces ¿Qué fracción del volumen de
agua es el volumen de vino al final?
A)
85
109
B)
125
218
C)
31
41
D)
43
31
E)
5
7
Solucion:
5 5 5 125
. .
7 7 7 343
vino al final T T 
218
343
agua al final 
( )
125
218
f agua vino
f


Clave: B.
EJERCICIOS DE EVALUACIÓN N° 8
1. ¿Cuántas fracciones propias e irreductibles de denominador 168 existen tales
que la suma de sus términos sea múltiplo de 11?
A) 5 B) 3 C) 4 D) 9 E) 6
Solucion:
N < 168 = 8.3.7
 N + 168 = 11
o
N toma 5 valores
N = 11
o
+ 8
Clave: A.
2. A una reunión asistieron 103 personas, de las cuales
4
15
de los hombres
bailaban y
1
7
de las mujeres usaban falda. ¿Cuántas mujeres no bailaban?
A) 16 B) 8 C) 7 D) 12 E) 3
Solucion:
H = 15k  15(3) = 75 HB =
4
15
(75) = 20
M = 7 L = 7 (4) = 28 M no bailan 8
103 Clave: B.
3. Se compró cierta cantidad de naranjas, la mitad del total a cinco por seis
soles, y la otra mitad restante, a seis por siete soles. Se vende los tres quintos
del total a tres por cinco soles y el resto a cuatro por siete soles. Si ganó 930
soles ¿Cuántas naranjas se vendió?
A) 1 600 B) 2 000 C) 1 800 D) 1 500 E) 1 200

27. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 27
Solucion:
Sea  naranjas = x
3 5 2 7 1 6 1 7
930
5 3 5 4 2 5 2 6
x x x x
        
           
        
x = 1800
Clave: C.
4. Si
1 13 33 61 397 y
+ + + +...+ = x
3 15 35 63 399 z
además y < z , Halle “x + y + z”
A) 28 B) 29 C) 34 D) 31 E) 24
Solucion:
1 1 1 1 1
10 1 ...
3 3 5 20 21
20 190 1
10 9
21 21 21
y
x
z
 
        
  
X + y + z = 31
Clave: D.
5. Un obrero realizo un trabajo en cuatro días; el primer día hizo una parte, el
segundo día hizo un tercio de lo que faltaba, el tercer día un cuarto del resto y
el cuarto día un tercio del total de la obra ¿Cuántos días menos emplearía si
trabajara con el rendimiento del primer día.
A) 2 B) 3 C) 4 D) 5 E) 1
Solucion:
i) p  p
ii)  
1 1 1
1
3 3 3
p p  
1 1 2
2 2 3
p  emplea 3 al día
iii)  
1 2 1 1
1
4 3 6 6
p p
 
   
 
1
3
p  1 día menos
Clave: E.
6. Se tiene dos velas de diferente longitud y calidad. La de mayor longitud se
consume en 7 horas y la otra en 10 horas. Después de 4 horas de estar
encendidas las dos velas tienen la misma longitud. A partir de este momento
¿Qué tiempo debe transcurrir para que la longitud de la vela que era de menor
longitud sea el doble de la otra?
A) 2h B) 3h C) 2.5h D) 1,5h E) 2,4h
Solucion:
En t hr: 1 2 1
6 3
t t 
   
 
3hr 6 hr t = 2
Clave: A.
h h

28. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 28
7. Tres grifos pueden llenar un tanque en 3; 4 y 5 horas trabajando solos. Se abre
el primero y al cabo de 45 minutos el segundo y luego de 30 minutos más el
tercero, tal que 15 minutos después se habrá llenado 354 litros ¿Cuál es la
capacidad del tanque en litros?
A) 450 B) 480 C) 680 D) 420 E) 540
Solucion:
1 3 1 1 1 1
. . . 354
3 2 4 4 5 4
x
 
   
 
 x = 480
Clave: B.
8. Halle el valor de
1 5 1 5
+ + + +...
6 36 216 1296
A)
4
3
B)
2
3
C)
11
35
D)
1
2
E)
5
3
Solucion:
 
 
 
6
6
6
15 11
0,15
55 35
k   
Clave: C.
9. Las dimensiones de un ladrillo de forma de paralelepípedo son
24
25
dm;
8
15
dm
y
16
35
dm ¿Cuántos ladrillos como mínimo se tendrán que utilizar para formar
un cubo compacto?
A) 3 450 B) 4 020 C) 3 906 D) 3 780 E) 3 800
Solucion:

3
48
5
3780
24 8 16
25 15 35
ladrillos
 
 
  
   
   
   
Clave: D.
10. Sea
1 1 1 1
R = + + + +...
2 6 12 20
de (n – 1) sumados y
1 1 1 1
F = + + + +...
3 15 25 63
de
 
 
 
n-2
2
sumandos además 
111
R F =
226
¿Cuál es el valor de n?
A) 110 B) 111 C) 100 D) 115 E) 113

29. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 29
Solucion:
1 1
1
1 2
2 1
1 1
n
R
n n
n
F
n n

  

  
 

1 2 111
. .
2( 1) 226
2 111
113
n n
R F
n n
n
n
 
 



 n = 11
Clave: E.
Álgebra
EJERCICIOS DE CLASE
1. Si  y son raíces del polinomio   3x5xxp 2
 , hallar el valor de
2
2











.
A)
3
5
B)
4
25
C)
25
9
D)
3
25
E)
2
55
Solución:
3
25
3
52
2)ii
52
3.
5)i
22222
22































Clave: D
2. Si el polinomio      m237xm312xxp 2
 tiene raíces iguales, hallar el
menor valor de m.
A)
9
10
 B) 1 C) 2 D)
10
9
E) 2
Solución:
 
     
   
2m
9
10
m
020m8m9
0m14214m9m614
0m2374m312
0entonces,igualesraícestienexp)i
2
2
2





Clave: A

30. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 30
3. Hallar la suma de las raíces del polinomio
      0ba;a3bxb3axxp 22
 .
A) 6 B)
a
b3
C)
b
a3
D) 6 E) 0
Solución:
    
      
      
0esraícesdeSuma
3y3:raíces
3x3xbabaxp
3xba3xbaxp
a3bxb3axa3bxb3axxp




Clave: E
4. Si a y b son las raíces de un polinomio mónico de segundo grado tales que:
      ,21b21a2y12b2a  hallar el coeficiente del término
lineal del polinomio.
A)
10
9
 B)
10
9
C)
10
7
D)
10
7
 E)
9
7
Solución:
        
  
  
 
 
 
10
9
eslinealomintérdelecoeficientEl
5
6
x
10
9
xxp
10
9
ba3ba2
5
6
4
3ba2ab4)iii
5
6
ab
3b2a2ab421b21a2
3b2a2ab12b2a)ii
abxbaxxpbxaxxp)i
2
2














Clave: A
5. Si m, n y q son las raíces del polinomio   qnxmxxxp 23
 ; 0n  , hallar el
valor de  3
qnm  .
A) 1 B) – 1 C) 0 D) 8 E) – 8

31. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 31
Solución:
 
 
    11qnm)ii
1mnmnqmnq
nnqnnqqnmnnqmqmn
nq0qnmqnm
entonces,xpderaícessonqyn,m)i
33




Clave: B
6. Si el polinomio   knxmxxxp 23
 ; 0mnk  tiene una de sus raíces igual
a la suma de las otras dos, calcular el valor de
k
mmn4
T
3

 .
A) 8 B) 2 C) 4 D) 6 E) 10
Solución:
 
   
     
   
       
 
8T
ab
ab8
T
baab
ba8baabba24
T)iv
baabkkbaab)iii
baabnnbabbaaab)ii
ba8mba2mmbaba
xpderaícessonbayb,a)i
32
2
33











Clave: A
7. Si 175  es raíz del polinomio    n,m;nmxx8xxp 23
Q, hallar
n3m2  .
A) 12 B) 18 C) 24 D) 28 E) 32
Solución:
 
      
   
    24163122n3m2)iv
16nn2175175)iii
12mm21752175175175)ii
2r8r175175
ry175,175:sonxpderaícesLas)i





Clave: C
8. Si i23  es raíz del polinomio    n,m;44nxmxxxp 23
R, hallar
n2m7  .
A) 6 B) 12 C) 16 D) 18 E) 24

32. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 32
Solución:
 
  
        
    1213227n2m7)iv
13nn121211
n4i234i23i23i23)iii
2mm4i23i23)ii
4r44ri23i23
ryi23,i23:sonxpderaícesLas)i






Clave: B
9. Si 2i es una raíz de   bx5axx2xp 23
 , hallar el valor de
2
13
a4b





 
.
A) – 4 B) 1 C) 4 D) 9 E) 16
Solución:
i)
2 a – 5 b
x = 2i 4i 2ai – 8 – 4a – 26i
2 a + 4i 2ai – 13 b – 4a –26i = 0
ii) i2
13
a4b
i26a4b0i26a4b 


  4i2
13
a4b 2
2





 

Clave: A
EJERCICIOS DE EVALUACIÓN
1. Determine la suma de los cubos de las raíces del polinomio
  3x3xxp 2
 .
A) 3 B) 33 C) 35 D) 36 E) 312
Solución:
 
   
 
  
312
33333
333
3)ii
3
3
y:sonxppolinomiodelraícesLas)i
33
33
33
33







Clave: E

33. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 33
2. Hallar el mayor valor entero de k para que el polinomio   4kxxxp 2

admita soluciones complejas.
A) – 4 B) 4 C) 3 D) 2 E) – 2
Solución:
  




max
2
2
k
4k4
16k
0414k
Clave: C
3. Determinar el valor de verdad de las siguientes proposiciones:
I. Si p(x) es un polinomio cúbico con coeficientes reales, entonces nunca
tiene raíces reales.
II. Si a + bi es una raíz del polinomio p(x) de grado 2 cuyos coeficientes no
son números reales, entonces a – bi también es raíz de p(x).
III. La suma de los coeficientes del polinomio mónico de menor grado
cuyas raíces son 3esi31 .
A) VVF B) FFF C) VVV D) FVF E) FFV
Solución:
I. El polinomio   1xxp 3

Tiene una raíz real x = 1 y dos raíces no reales (F)
II. El polinomio     ixi1xxp 2

Tiene una raíz real x = 1 y una raíz imaginaria x = i (F)
III.     i31xi31xxp 
  4x2xxp 2

3421escoeficient  (V)
Clave: E
4. Si 1 y – 1 son raíces de     1nx3nxxqymxx2xp 22

respectivamente y  es una raíz común de ambos, hallar   1q .
A)
2
11
B) 5 C)
2
5
D)
2
15
E)
2
3
Solución:
Z = 3

34. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 34
   
 
    
 
    
 
2
11
2
1
61q)iv
2
1
comúnraízunaes
2
1
x1x2escomúnfactorEl)iii
1x1x2xq
1x3x2xq
1x1x2xp
1xx2xp)ii
2n01q,1m01p)i
2
2









Clave: A
5. Si – 1 es raíz del polinomio    xx5x2xp 23
y el producto de sus
otras raíces es – 1; además 0x es la menor raíz de p(x), hallar 0x .
A) 1 B) 0 C) – 2 D) – 1 E) 2
Solución:
i) Las raíces de p(x) son: – 1 , a y b con ab = –1
2
3
ba
2
5
ba1 
 
 
 
    
  1221x)iv
2x
2
1
x2x1xxp
2xx5x2xp
2
2
ab1)iii
1
2
1
2
3
2
abba
2
abba)ii
0
0
23

























Clave: A
6. Si a, b y c son raíces del polinomio mónico   223
bcxbxaxxp  ; b > 0,
calcular 222
cba  .
A) 1 B) – 1 C) 0 D) 2 E) – 2
Solución:
i) Las raíces del polinomio p(x) son: a, b y c
1cbcb11apero
a
b
cba 

35. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 35
   
 
  1111111cba)iii
1b1b0b01bb0bb
bbb1b1
a
b
abc)ii
222222
2
22
2



Clave: B
7. Si r Z y 23  son dos raíces del polinomio
     b;14xb67x8xxp 23
R , hallar el valor de 5r + 4b.
A) 6 B) – 1 C) 9 D) – 4 E) 2
Solución:
 
        
    28102425b4r5)iv
2bb672232232323)iii
2r8r2323)ii
r;23,23sonxppolinomiodelraícesLas)i




Clave: E
8. Si 21 es una raíz del polinomio   7axbxx2xp 23
 ; b,a Q, hallar el
valor de
1
b
a
a
b
M







 .
A)
23
132
B)
23
112
C)
23
122
D)
23
142
E)
23
152
Solución:
 
  
      
23
132
ab
ab
ab
ab
b
a
a
b
M)v
12a
2
a
2
7
21
2
7
212121)iv
11b
2
b
2
7
2121)iii
2
7
r
2
7
r2121)ii
ry21,21:sonxppolinomiodelraícesLas)i
22
1221










 
























Clave: A
9. Si 1 + 2i, a y b, (a < b) son las raíces del polinomio
       i212xi21xi12xxp 23
 , hallar  b2a3p  .
A) 4 – 4i B) 4 + 4i C) 4i D) 4 E) – 4

36. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 36
Solución:
i) Las raíces del polinomio p(x) son: bya;i21
ii)
1 i22  i21 i42 
i21x  i21 i21 i42 
1 1 2 0
1x  1 2
1 2 0
1b2a32b,1a,i21:raíces
2x


iii)          i2121i211i1211p 23

  i41p 
Clave: C
Geometría
EJERCICIOS DE CLASE Nº 8
1. En la figura, L1 // L 2 // L 3 y L 4 // L 5. Si AQ = EF = 4 cm, FG = 2HI = 6 cm y CI =
3HF, halle DE.
A) 5 cm
B) 4 cm
C) 6 cm
D) 7 cm
E) 3 cm
Solución:
1) Thales:
3
EH
=
6
4
 EH = 2
2) AQD ~ HEF (A-A-A)

2
4
=
4
QD
 QD = 8
3) Thales en el BFQ: (L4 // L5)

37. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 37
8x
4

=
k3
k
 x = 4 cm
Clave: B
2. En la figura, mMAC = mBNM y numéricamente BN · AC = 4AB. Halle MN en metros.
A) 1 m
B) 5 m
C) 2 m
D) 3 m
E) 4 m
Solución:
1) El MBN ~ ABC (A-A-A)

AC
MN
=
AB
BN
 MN =
AB
AC·BN
=
AB
AB·4
= 4 m
Clave: E
3. En la figura, AB = 3 cm, BC = 4 cm y AD = DC. Halle DE.
A)
8
17
cm
B)
7
15
cm
C)
8
15
cm
D)
8
13
cm
E) 2 cm
Solución:
1) BDE ~ ABC

3
DE
=
4
2
5

38. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 38
 DE = x =
8
15
cm
Clave: C
4. En la figura, AB //CE, BM = MF, PE = 3 m y MD = 3PD. Halle AB.
A) 18 m
B) 12 m
C) 21 m
D) 16 m
E) 15 m
Solución:
1) Se traza MN // AB
2) PDE ~ MDN
x
3
=
a3
a
 x = 9
3) AB = 2x = 18 m
Clave: A
5. En la figura, AB = 16 m, BC = 4 m y AD = 6 m. Halle ED.
A) 1,5 m
B) 1,2 m
C) 2 m
D) 4 m
E) 3,5 m
Solución:
1)  +  = 90°  mABD = 
2) En el ABC: T.B.I.
BC
AB
=
EC
AE






kEC
k4AE
3) En el ADE: T.B.E.

39. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 39
x
6
=
k
k5
 x = 1,2 m
Clave: B
6. En la figura, BE = 4ME y AC = 4 cm. Halle el perímetro del triángulo ABC.
A) 13 cm
B) 14 cm
C) 16 cm
D) 20 cm
E) 12 cm
Solución:
1) Como BE = 4ME 





k3BM
kME
2) M es incentro, teorema:
k
k3
=
4
BCAB 
 AB + BC = 12
 PABC = 12 + 4 = 16 cm
Clave: C
7. En la figura, MN // AC y AC = 9 m. Halle AP.
A) 4,8 m
B) 5,4 m
C) 4 m
D) 4,5 m
E) 6 m
Solución:
1) T. de Thales:
MA
BM
=
NC
BN
2) Teorema de Ceva:
b · ak(9 – x) = a ·bk · x
x = 4,5 m Clave: D

40. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 40
8. En la figura, G es baricentro del triángulo ABC. Si GE = 1 m y ED = 3 m, halle x.
A)
2
37
B) 45°
C)
2
53
D)
2
45
E) 30°
Solución:
1) Trazar BM : mediana
2) Trazar FM  AC  BDG ~ BEG (A-A-A)
 BG2
= 4 · 1, BG = 2
3)
GE
BG
=
FM
BM

1
2
=
FM
3
, FM =
2
3
 x =
2
53
Clave: C
9. En la figura, ABCD es un romboide, AE y DF son bisectrices de BAD y ADC
respectivamente. Si AB = 4 m y BC = 6 m, halle EF.
A)
3
2
m
B)
5
6
m
C)
4
3
m
D)
3
4
m
E)
5
4
m

41. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 41
Solución:
1)
ED
BE
=
6
4
(T.B.I.)
AF
CF
=
6
4
(T.B.I.)
2) EF //BC
3) EOF ~ BOC

6
x
=
m5
m
 x =
5
6
m
Clave: B
10. En la figura, AC = b, PQ = a y BH = c, halle BD.
A)
b
ac
B)
c
ab
C)
a
bc
D)
b
c)1a( 
E)
c
b)1a( 
Solución:
1) mBPQ =  + 
2) ABC ~ PBQ (A.A.A.)
3)
PQ
BD
=
AC
BH

a
BD
=
b
c
 BD =
b
ac
Clave: A
11. En la figura, BD = 5 m, AE = 4 m y CF = 12 m. Halle mABC.
A) 36°
B) 72°
C) 74°
D) 76°
E) 82°

42. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 42
Solución:
1) AEB ~ CFB 
BC
AB
=
12
4
=
3
1
2) T.B.I.
n
m
=
3
1
3) Trazamos HD  AB
4) AHD ~ AFC 
12
HD
=
nm
m

=
4
1
 HD = 3
5) En BHD:  = 37°
2 = 74°
Clave: C
12. En un triángulo rectángulo ABC, la mediatriz relativa a la hipotenusa interseca a BC
en M. Si AC = 6 m y BC = 5 m, halle
AM
BM
.
A)
9
5
B)
6
1
C)
18
7
D)
5
2
E)
5
3
Solución:
1) AMC es isósceles  AM = MC
2) ABC ~ MHC
MC
6
=
3
5
 MC = 3,6 = AM
 BM = 5 – 3,6 = 1,4

AM
BM
=
18
7
Clave: C
13. En la figura, AB = 16 m y BC = 4 m. Si
MP
BM
=
3
1
, halle QB.
A) 2 m
B) 2,5 m
C) 1 m
D) 1,5 m
E) 1,8 m

43. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 43
Solución:
1) T.B.I.:
PC
AP
=
BC
AB






aPC
a4AP
2) T. Menelao
(16 – x)b · a = x · 3b · 5a
 16 – x = 15x
x = 1 m
Clave: C
14. En un triángulo ABC, AB = a cm, BC = (a + 2) cm y AC = (a + 1) cm, a > 0. Halle la
longitud del segmento que une el incentro con el baricentro.
A)
3
1
cm B)
2
1
cm C)
3
2
cm D)
2
3
cm E) 2 cm
Solución:
1) T. Incentro:
1a
)2a(a


=
ID
BI

ID
BI
=
1
2
 IG //DM
2) T.B.I.:
2a
a

=
n
m
 m =
2
a
 DM =
2
1
3) BIG ~ BDM
2
1
x
=
k3
k2
 x =
3
1
Clave: A
EJERCICIOS DE EVALUACIÓN Nº 8
1. En la figura, AB = 5 cm, BC = 6 cm y AC = 7 cm. Si PQ// AC, PR //BC y RT // AQ,
halle TC.
A)
25
33
cm B)
35
24
cm
C)
23
15
cm D)
24
35
cm
E)
12
35
cm

44. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 44
Solución:
1) T.B.I. 5k + 7k = 6  k =
2
1
 BQ =
2
5
 QC =
2
7
2) T. Thales:
QC
BQ
=
PA
BP
=
RA
CR
=
7
5
3) Thales:
TC
QT
=
RC
AR

x
x
2
7

=
5
7
x =
24
35
cm
Clave: D
2. En la figura, AM = MC, AH = 3 cm, BC = 8 cm y AC = DE. Halle CE.
A) 14 cm
B) 16 cm
C) 18 cm
D) 20 cm
E) 22 cm
Solución:
1) En ABC: HM: base media
 HM =
2
BC
=
2
8
= 4
2) En AHM:
AM = 5 = BM
3) BMC ~ EDC
10
5
=
x
8
 x = 16 cm
Clave: B

45. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 45
3. En la figura, O es circuncentro del triángulo ABC. Si AO = 2BE, EO = 2 m y CD = 16 m,
halle BE.
A) 1 m
B) 2 m
C) 2,5 m
D) 3 m
E) 4 m
Solución:
1) Trazar OC  OC = OA = 2x
2) mAOC = 2 (propiedad)
3) AEB ~ DCO

x2
x
=
16
2x2 
 x = 3 m
Clave: D
4. En la figura, AB = 6 cm, BC = 8 cm, AC = 7 cm, I incentro y DC = CE. Halle BF.
A) 6,2 cm
B) 6,4 cm
C) 4,6 cm
D) 4 cm
E) 5,2 cm

46. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 46
Solución:
1) En el ABC: T. del incentro
b
a
=
7
86 
=
1
2
2) En el DBC: T. de Menelao
b · x · m = a(8 – x)2 m

x8
x

= 





b
a
2
 x = 6,4 cm
Clave: B
5. En la figura, BD = AE, AB = 9 m y DE = 4 m. Halle DC.
A) 26 m
B) 20 m
C) 18 m
D) 15 m
E) 21 m
Solución:
1)  +  = 90°
2) En el ABD: T.B.I.:
k
9
=
4
k
 k = 6
 T.B.E.:
6
9
=
x
10x 
 x = 20 m
Clave: B
6. En un triángulo ABC se trazan la bisectriz interior AD , la mediana BM y la ceviana
CE, concurrentes en el punto O. Si AB = 4 m y AC = 6 m, halle EB.
A) 2,5 m B) 2,1 m C) 1,6 m D) 1,8 m E) 1,4 m

47. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 47
Solución:
1) T.B.I.
AB
AC
=
DB
CD
 DB = 2k y CD = 3k
2) Por el teorema de Ceva:
x · 3k · 3 = (4 – x)2k · 3
x = 1,6 m
Clave: C
Trigonometría
EJERCICIOS DE LA SEMANA Nº 8
1. Los ángulos  y  son agudos con  menor que  , tales que la razón de sus
tangentes es
18
7
y
5
4
)(sen  . Calcule )(sen25  .
A) 4,8 B) 7,6 C) 5,4 D) 8,8 E) 6,6
Solución:
k18sencos,k7cossen
18
7
sencos
cossen
18
7
tg
tg






.
Además se tiene que
5
4
sencoscossen)(sen  , entonces
125
4
k
5
4
k18k7  , luego,
125
44
125
4
11k11k7k18sencoscossen)(sen 






8,8
5
44
)(sen25 
Clave: D
2. Con los datos de la figura, halle tg .
A) –
7
3
D) –
6
5
B)
6
5
E)
7
3
C) –
7
4

48. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 48
Solución:
 ,
2
1
tg,
2
3
tg 
Luego,
7
4
4
7
1
4
3
1
2
1
2
3
2
1
2
3
1
2
1
2
3
)(tgtg 


























Clave: C
3. Si  zyx y 0zcosycosxcos  , halle zctgyctg  .
A) 1 B) 2 C)
4
1
D)
2
1
E)
2
1

Solución:
xzy  , zcosycosxcos 
zcosycoszsenysenzcosycosxcos)zycos( 
2
1
zctgyctgzsenysenzcosycos2 
Clave: D
4. Al simplificar la expresión
x4tgx5tg1
)xtgx2tg1)(x4tgx5tg(


,
se obtiene
A) x2sec B) x2tg C) tgxx2sec  D) xsectgx  E) x2secx2tg 
Solución:
xtgx2tg)tgxx2tg1(xtg
x4tgx5tg1
)xtgx2tg1)(x4tgx5tg(



xtgx2sec
xcosx2cos
xsen
xcos
xsen
x2cos
x2sen



Clave: C
5. Si
5
3
)yx(tg  y 3y3tg  , halle )y2x(tg2  .
A) 9 B) 7 C) 5 D) 5 E) 7

49. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 49
Solución:
2
9
5
3
31
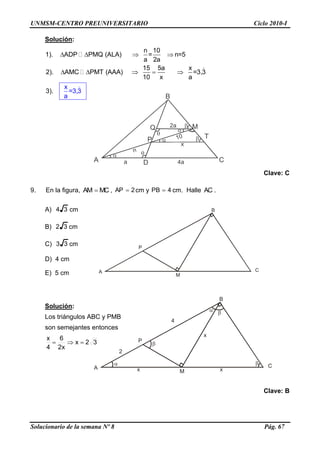
3
5
3
y3tg)yx(tg1
y3tg)yx(tg
]y3)yx[(tg)y2x(tg 












9)y2x(tg2 
Clave: A
6. Si 2)32x(tg  y  30yx , halle el valor de )13yx2(tg
635
13







.
A) 4 B) 2 C) 1 D) 1 E) 2
Solución:



30tg)13x(tg1
30tg)13x(tg
)]yx()13x[(tg)13yx2(tg … (1)
Por otro lado,
3
1
21
12
)13x(tg45)32x(13x 


 … (2)
Luego, de (2) en (1) se tiene
13
635
26
12310
133
33
3
1
3
1
1
3
1
3
1
)13yx2(tg






















1)13yx2(tg
635
13










Clave: C
7. Un triángulo de ángulos internos , y  , satisface la relación 1
5
tg
3
tg




.
Calcule ctg .
A)
2
1
B)
6
7
 C)
7
6
 D)
7
6
E)
4
7
Solución:



tgtg1
tgtg
tg)(tgtg)(180180
4
7
ctg
7
4
151
53
tg 


 .
Clave: E

50. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 50
8. Simplifique la expresión







 
50tg10ctg
2
40tg50tg 22
A) 40tg2
B) 40ctg2
C) 40tg D) 50tg E) 50ctg
Solución:
2
40tg50tg
40tg50tg1
40tg50tg
)4050(tg10tg




 .
Luego









 
50tg10ctg
2
)40tg50tg(
)40tg50tg(50tg10ctg
2
40tg50tg 22
 50tg10ctg10tg)40tg50tg(
 40tg
Clave: C
9. Si  2cba y ccosbcosacos  , calcule ctgbtg  .
A)
2
1
B) 2 C) 1 D) 4 E)
4
1
Solución:
csenbsenccosbcos)cbcos(acos)cb(2a 
csenbsenccosbcos2ccosbcoscsenbsenccosbcos 
2
ccosbcos
ccosbcos2
ctgbtg 


 .
Clave: B
10. Si  mctgk12tg112tg33tg , donde 0k  y 160m100  , calcule m – k.
A) 120 B) 144 C) 149 D) 122 E) 151
Solución:
 12tg)12tg33tg1(12tg112tg33tg



 12tg
45tg
)12tg33tg(
 33tg
 57ctg
)57180(ctg 
 123ctg
Luego, 1221123km 
Clave: D

51. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 51
EVALUACIÓN Nº 8
1. Si 0cossenc)(senb)(sena  , halle  tgctg .
A)
ab
cba


B)
ab
cba


C)
ab
cba


D)
ba
cba


E)
ba
cab


Solución:
0cossencsencosbcossenbsencosacossena 
 tgctg)ab(cba0ctgctgbbtgctgaa
ab
cba
tgctg


 .
Clave: C
2. Simplifique la expresión
)ctg1)(tg1(
)cos()(sen


A)  cscsec B)  sencos C)  cscsec
D)  tgsec E)  sencos
Solución:
)cossen)(cossen(
sencos)sensencoscossencoscossen(
)ctg1)(tg1(
)cos()(sen








sensencoscossencoscossen
sencos)sensencoscossencoscossen(
 sencos
Clave: E
3. Considerando los datos de la figura y 25,0)(tg  , halle el valor de x.
A) 100
B) 103
C) 97
D) 106
E) 99

52. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 52
Solución:
Tenemos
4
1
)(tg  ,
4
3
tg  y
4
3x
)(tg

 , luego,
13
16
tg
tg
4
3
1
4
3
tg
)(tg
4
1



 .
Como
4
3x
)(tg

 se tiene
100x1033x
4852
)16(4)13(3
4
3x
4
3x
13
16
4
3
1
13
16
4
3






















Clave: A
4. Si
)cos(
)(sen
ctg


 , halle tg .
A)
)(sen
)(sen


B)
)cos(
)cos(


C)
)cos(
)(sen


D)
)(sen
)cos(


E) )(tg 
Solución:
Tenemos,









tgctg
tgctg1
sensencoscos
sencoscossen
)cos(
)(sen
ctg
 ctgctg1)ctgctg(tgtgctg1ctgtgctgctg
)(sen
)cos(
sencoscossen
sensencoscos
ctgctg
1ctgctg
tg









Luego,
)(sen
)cos(
tg



Clave: D
5. Si
5
52
x3sen  , donde 3x es un ángulo agudo; calcule el valor de la expresión
x3ctgx4tgx3tgtgxxtgx4tg 
A) 1,5 B) 2,5 C) 3,5 D) 4,5 E) 5,6
Solución:
x3ctgxtgx4tgx3tg]xtgx4tg1)[xx4(tgx3ctgx4tgx3tgtgxxtgx4tg 
x3ctgxtgx4tgx3tgxtgx4tgx3tgx3tg 
x3ctgx3tg 

53. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 53
M
M S M
M S E S M
M S E R E S M
M S E R P R E S M
M S E R E S M
M S E S M
M S M
M
0
0 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 0
0
M
M S M
M S E S M
M S E R E S M
M S E R P R E S M
M S E R E S M
M S E S M
M S M
M
0
0 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 1 0
0 1 0
0
x3cscx3sec 
Como
5
52
x3sen  , entonces 5,2
10
25
20
5
5
5
x3cscx3sec 












Clave: B
Habilidad Lógico Matemática
EJERCICIOS DE CLASE Nº 8
1. En el siguiente arreglo de letras, ¿de cuántas formas distintas se puede leer
PRESM10 a igual distancia de una letra a otra en cada lectura?
A) 252
B) 259
C) 261
D) 270
E) 248
Solución:
P  Nro Formas “P” = 1
R
RPR
R
 Nro formas “PR” = 4(1) = 4(21
– 1)
E
ERE
ERPRE
ERE
E
 Nro formas “PRE” = 4(3) = 4(22
– 1)
 Nro formas “PRESM10” = 4(26
– 1) = 252
Clave: A

54. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 54
2. En la secuencia de figuras, ¿cuántos triángulos que posean exactamente dos
vértices que sean centros de los círculos sombreados hay en total en la figura 74?
figura 1 figura 2 figura 3 figura 4
A) 2775 B) 5442 C) 5550 D) 5700 E) 5505
Solución:
figura 1 figura 2 figura 3 figura 4
Fig. 1: 2 = 1(2)
Fig. 2: 6 = 2(2 + 1)
Fig. 3: 12 = 3(3 + 1)
Fig. 4: 20 = 4(4 + 1)

Fig. 74: (74)( 75) = 5550
Clave: C
3. En la figura se tiene 100 circunferencias. ¿Cuántos puntos de intersección existen
entre ellas?
A) 396
B) 394
C) 395
D) 398
E) 392
Solución:

55. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 55
1) Analizando:
Para 3 circunferencias:  
1
Nº ptos de inters 2 4
Para 4 circunferencias:   
2
Nº ptos de inters 2 4 4
Para 5 circunferencias:    
3
Nº ptos de inters 2 4 4 4
Para 100 circunferencias:
98
Nº ptos de inters 2 4 4 4    
2) Entonces en 100 circunferencias hay 394 puntos de intersección distintos.
Clave: B
4. En el siguiente arreglo, ¿de cuántas formas distintas se puede leer INTELIGENTE a
igual distancia de una letra a otra en cada lectura?
A) 258
B) 254
C) 252
D) 250
E) 256
Solución:
1) Por inducción
Para 3 letras:
1 1
1 2
I N
#deformasdeleer:INT 3
N T
 
Para 5 letras:
1 1 1
1 2 3
1 3 6
I N T
N T E #deformasdeleer:INTEL=6
T E L

Para 7 letras:
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20
I N T E
N T E L
#deformasdeleer:INTELIG=20
T E L I
E L I G

I N T E L I
N T E L I G
T E L I G E
E L I G E N
L I G E N T
I G E N T E
I N T E L I
N T E L I G
T E L I G E
E L I G E N
L I G E N T
I G E N T E

56. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 56
2) Fórmanos el triangulo de Pascal
1 1 1 1 1 1
1 2 3 4 5 6
1 3 6 10 15 21
1 4 10 20 35 56
1 5 15 35 70 126
1 6 21 56 126 252
3) Numero formas de leer INTELIGENTE: 252
Clave: C
5. Las figuras que se muestran están construidas con palitos negros y blancos, los
palitos negros en los bordes y los palitos blancos en el interior. Si todas las figuras
corresponden a un rectángulo 3 filas por n columnas, ¿cuántos palitos blancos se
han utilizado en la figura 2011?
1 2 3

A) 10058 B) 10050 C) 10054 D) 10052 E) 10056
Solución:
1 2 3

1) Por inducción
En la figura 1: hay 2 palitos blancos 2 5 0  
En la figura 2: hay 7 palitos blancos 2 5 1  

57. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 57
En la figura 3: hay 12 palitos blancos 2 5 2  
2) Por tanto en la figura 2011 20102 5 10052    palitos blancos
Clave: D
6. Halle la suma de las cifras, de la suma de las cifras de
 
2010 cifras
M 123456789 999...999
A) 18 B) 27 C) 36 D) 81 E) 10
Solución:
 
2010 cifras
M 123456789 999...999
2010
9cifras 2010cifras
M 123...789X(10 1)
M 123456788999....9999876543211
 

suma de cifras de M =18090
la suma de cifras, de la suma de cifras de M =18
Clave: A
7. La siguiente secuencia de castillos está formado por cartas de naipes. Halle el
número de cartas del castillo de la figura 30.
A) 1363
B) 1368
C) 1364
D) 1365
E) 1366
figura 1 figura 2 figura 3
. . .

58. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 58
Solución:
1) Figura 1:  1 2 1S  .
2) Figura 2:  2
1 2
2 1 2 1 2 3
2
S

      .
3) Figura 3:  3
2 3
2 1 2 3 1 2 3 4
2
S

        .
4) Figura 4:  4
3 4
2 1 2 3 4 1 2 3 4 5
2
S

          .
5) Figura 30: 30
29 30
30 31 1365
2
S

    .
Clave: D
8. En las figuras se muestran círculos tangentes entre sí, unas sombreadas y otras sin
sombrear. ¿Cuántos círculos sombreados existen en la figura 99?
figura 1 figura 2 figura 3 figura 4
A) 2750 B) 2752 C) 2756 D) 2760 E) 2754
Solución:
figura 1 figura 2 figura 3 figura 4
Numero de círculos sombreados figura 1:   2 1 1 2 .
Numero de círculos sombreados figura 2:   2 2 1 2
Numero de círculos sombreados figura 3:    2 2 1 2 3
Numero de círculos sombreados figura 4:    2 3 1 2 3
Numero de círculos sombreados figura 5:     2 3 1 2 3 4
Numero de círculos sombreados figura 6:     2 4 1 2 3 4
Numero de círculos sombreados figura 2n-1:          2 1 2 3 4 5 ... 1n n
figura 1 figura 2 figura 3
. . .

59. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 59
Numero de círculos sombreados figura 2n:             2 1 1 2 3 4 5 ... 1n n
Por tanto, numero de círculos sombreados figura 99=2(50)-1:
 
 
          
 
51 52
2 50 1 2 3 4 5 ... 51 2 50 2752
2
Clave: B
9. Dos obreros con diferentes eficiencias, trabajan en una misma obra. Estos obreros
trabajando juntos harían toda la obra en 12 días. Después de cierto tiempo de
trabajar juntos, el menos eficiente se enferma y el otro termina la obra 12 días
después. Si el menos eficiente trabajando solo terminaría la obra en 36 días, ¿a los
cuántos días de iniciada la obra se enfermó?
A) 2 B) 4 C) 6 D) 8 E) 10
Solución:
1º Sea A más eficiente que B
2º como B hace solo en 36 días, entonces en 1 día hace
1
36
de obra
3º supongamos que A hace en un día
1
a
de obra
Luego por dato los dos en 1 día harán:
1 1 1 1 1
12 a 36 a 18
    de obra
4º sea X el tiempo que trabajan junto(en luego de esto se enferma)
Entonces:
1 1
X x 12x 1
12 18
  , asi X=4.
Clave: B
10. Una bomba extrae toda el agua de un pozo en
7
2
4 días; otra lo hace en
13
4
2 días
y una tercera en
8
7
1 días. Calcule el tiempo que se tardaría en extraer toda el agua
del pozo haciendo funcionar las tres bombas a la vez.
A) 15 h B) 22 h C) 20 h D) 18 h E) 36 h
Solución:
hdTVVT
V
V
Q
V
V
Q
V
V
Q
20
6
5
30
16
30
13
30
7
30
16
1
30
13
2
30
7
4
8
73
13
42
7
21




















Clave: C

60. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 60
11. Un hombre que rema un bote a una velocidad constante, remonta contra la corriente
de un rio que fluye a una velocidad también constante. Al pasar bajo un puente
angosto, pierde su sombrero. El hombre se da cuenta de la perdida media hora más
tarde, da entonces media vuelta y recupera su sombrero a 2 km más abajo del
puente. ¿Cuál es la velocidad de la corriente?
A) 2
km
h
B) 3
km
h
C) 1
km
h
D) 4
km
h
E) 5
km
h
Solución:
1) Velocidad de la corriente del rio: rv
Velocidad del bote: bv
Tiempo de alcance:t
2) Tenemos las relaciones:
1
2
2
r rv tv 
   
1
2
2
b r b rv v t v v   
3) Resultan:
1
2
t h y 2km/hrv  .
Clave: A
12. Dos atletas están separados 300 m. Si estos atletas corren al encuentro, este se
produce al cabo de 20 segundos; pero si corren el uno en pos del otro, el alcance se
produce a los 60 segundos. Halle la velocidad del atleta más rápido.
A) 12
m
s
B) 11
m
s
C) 10
m
s
D) 8
m
s
E) 9
m
s
Solución:
1) Velocidades de los atletas: 21,vv
2) Tenemos las relaciones:
 1 220 300v v 
 2 160 300v v 
3) Resultan: 1 5m/sv  y 2 10m/sv  .
Clave: C
13. En la figura, AM es la mediana y DC = 4AD. Si AP = 10 cm, halle PM.
A) 10 cm
B) 20 cm
C) 18 cm
D) 22 cm
E) 17 cm A
B
CD
M
P

61. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 61
Solución:
   
1). Trazar QM//AC
10 x
2). ADP PMQ (ALA) = x=20
x
a
=
2a
3) 20. cm
Clave: B
14. En la figura, 3AB = 2BC y BT = 16 cm. Halle TR.
A) 6 cm
B) 4 cm
C) 12 cm
D) 8 cm
E) 10cm
Solución:
 Prolongamos AT hasta R
 ABR isósceles  BM = 2m

RC
BR
TR
BT
 
m
2m
TR
16
 ,
 TR = 8 cm
Clave: D
A C
B
R
 
T
A
B
C
M
D
P
Q
10
x
a 4a
2a




A C
B
R
 
T
P
162m
3m
2m
m
R

62. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 62
EVALUACION DE CLASE Nº 8
1. Calcule la suma de todos los números del siguiente arreglo
A) 2650 B) 2460 C) 2660 D) 2760 E) 2860
Solución:
Suma: 1 (2) + 2(3) + 3 (4) + 4(5) + ...+ 19 (20) = 19x20x21/3 = 2660
Clave: C
2. Determine la suma de cifras después de efectuar el producto
2010 cifras 2010 cifras
9999...992 9999...998
A) 18088 B) 19099 C) 18079 D) 18097 E) 18106
Solución:
2010 cifras 2010 cifras
9999...992 9999...998
1) Para 2n  cifras: 92 98 9016  .
2) Para 3n  cifras: 992 998 990016  .

63. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 63
3) Para 4n  cifras: 9992 9998 99900016  .
4) Para 2010n  cifras: cifras del Producto 9 2009 7 18088    .
Clave: A
3. En el siguiente arreglo numérico triangular, halle la suma de cifras del término
central de la fila 21.
1
3 5
7 9 11
13 15 17 19
21 23 25 27 29
.
.
.
.
.
.
fila 1
fila 2
fila 3
fila 4
fila 5
A) 9 B) 11 C) 6 D) 13 E) 14
Solución:
1
3 5
7 9 11
13 15 17 19
21 23 25 27 29
.
.
.
.
.
.
fila 1
fila 2
fila 3
fila 4
fila 5
Suma de extremos de  1 :1 1 2F
Suma de extremos de    
2
2 : 3 5 8 2 2F
Suma de extremos de    
2
3 : 7 11 18 2 3F
Suma de extremos de    
2
4 :13 19 32 2 4F
Suma de extremos de         
2
4 1 21: 2 21 2 441 2 441F a a
La fila F21 es impar  tiene termino central
 Termino central de   21 1 21 441F a a
Suma de cifras (441) = 9
Clave: A

64. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 64
4. ¿Cuántos cuadriláteros se pueden contar en la siguiente figura?
1
2
3
4
.
.
.
29
30
A) 119 B) 116 C) 113 D) 108 E) 121
Solución:
1
2
3
4
.
.
.
29
30
Números de cuadriláteros
En 1 figura: 3
En 2 figuras: 3 +
4
En 3 figuras: 3 +
4 + 4
En 4 figuras: 3 +
4 + 4 + 4 = 3 + 4(4-1)
En 20 figuras: 3 + 4(20-1)
En 30 figura: 3 + 4(30-1) = 119
Clave: A
5. Si en la figura n, de la secuencia mostrada, la suma de los números de las esquinas
superior derecha e inferior izquierda es 724, halle n.
, , , ...
figura 1
2
4
6
8
2
4
6
8
10
12 18
16
14
2
4
6
8
10
12
14
16 24 32
30
28
2618
20
22
figura 2 figura 3
A) 20 B) 19 C) 18 D) 17 E) 16

65. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 65
Solución
, , , ...
figura 1
2
4
6
8
2
4
6
8
10
12 18
16
14
2
4
6
8
10
12
14
16 24 32
30
28
2618
20
22
figura 2 figura 3
1.- Tenemos:
, , , ...Fig. 1 Fig. 2 Fig. 3
2
4
6
8
2
4
6
8
10
12 18
16
14
2
4
6
8
10
12
14
16 24 32
30
28
2618
20
22
2.- Por inducción:
Fig. 1:  2
6 4 10 2 5 2 12       
Fig. 2:  2
6 10 14 20 2 10 2 13        
Fig. 3:  2
6 14 20 26 34 2 17 2 14         
3.- Entonces:  
2
2 1 181Figura n n n     
 
 .
Clave: C
6. Un balde está lleno de un líquido. Se retira del balde los 2/3 de su contenido menos
20 litros. En una segunda operación se saca los 2/5 del resto y por último los
42 litros restantes. ¿Cuál era el contenido del balde?
A) 140 litros B) 150 litros C) 210 litros D) 144 litros E) 222 litros
Solución:
1º Sea la capacidad del cubo: v
2º retira: (2/3)v-20 queda: (1/3)v+20

66. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 66
M E EM160 m 20 m
t
t
3º retira: (2/5)[(1/3)v + 20] queda: (3/5)[(1/3)v + 20]=42
4º como: (3/5)[(1/3)v + 20]=42, entonces V=150
Clave: B
7. Después de una discusión entre Mario y Elizabeth, y cuando Elizabeth ya había
caminado 160 m; en ese instante Mario sale a perseguirla. Si se sabe que cada 20
segundos, Mario da 60 pasos de 70 cm cada uno, y Elizabeth en ese mismo tiempo,
da 28 pasos de 50 cm cada uno, ¿después de cuánto tiempo de partir Mario estará a
20 metros de Elizabeth?
A) 1min 20s B) 1min 30sC) 1min 40s D) 1min 50s E) 1min 42s
Solución:
1) En el esquema:
2) Velocidad de Mario:
60 70 21
/
20 10
Mario
cm
V m s

 
3) Velocidad de Elizabeth:
28 50 14
/
20 10
Elizabeth
cm
V m s

 
4) Como los tiempo son iguales, se tiene:
21 7
20 160
10 10
t t  
14
140 100 1min 40
10
t t segundos s   
5) Por tanto Mario estará a 20 metros de Elizabeth en 1min 40 segundos.
Clave: C
8. En la figura, PT || AC, BM = MC y DC = 4AD. Si PM = 10 cm, halle
PT
AD
.
A) 3,5
B) 3,4
C) 3,3
D) 3,2
E) 3,5
A
B
CD
M
P T

67. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 67
A
B
C
M
P
A
B
C
M
P
x
x
x
4
2





Solución:
   
    
n 10
1). ADP PMQ (ALA) = n=5
a 2a
15 5a x
2). AMC PMT (AAA) =3
x
,3
10 x
=3
a
3). ,3
a
Clave: C
9. En la figura, MCAM  , 2AP  cm y 4PB  cm. Halle AC .
A) 34 cm
B) 32 cm
C) 33 cm
D) 4 cm
E) 5 cm
Solución:
Los triángulos ABC y PMB
son semejantes entonces
32x
x2
6
4
x

Clave: B
A
B
C
M
D
P
Q
T10
n
a 4a
2a
x







68. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 68
Lenguaje
EVALUACIÓN DE CLASE Nº 8
1. Marque la alternativa en la que se presenta enunciado correcto.
A) Algunos signos lingüísticos están constituidos por el significado.
B) Todos los semantistas confeccionan diccionarios de las lenguas.
C) El semema es la unidad de estudio de la semántica lingüística. *
D) El fonema contiene el significado principal de una lengua natural.
E) La lexicología es la disciplina que estudia la estructura lingüística.
Clave: C. Todo semema es la unidad básica de significado, objeto de estudio de la
semántica. Es el conjunto de todos los semas evocados por un signo lingüístico en
un contexto determinado.
2. La semántica lingüística describe y explica
A) cómo se seleccionan y ordenan los datos léxicos.
B) los significados y sentidos de los signos lingüísticos. *
C) todos los signos en los diferentes campos de estudio.
D) solo los significados en el proceso diacrónico.
E) la estructura morfológica de las unidades léxicas.
Clave: B. La semántica tiene como tarea describir y explicar el significado o
significados y los sentidos de los signos lingüísticos.
3. El estudio del repertorio léxico de la lengua corresponde a la disciplina
lingüística denominada
A) fonología. B) morfología. C) semiótica.
D) lexicografía. E) lexicología.*
Clave: E. La lexicología estudia la estructura y funcionamiento del repertorio léxico
de la lengua.
4. Señale la opción donde las palabras de la serie comparten un mismo lexema.
A) Cámara, cama, cántico, encantado
B) Preclásico, clasifica, clasificar, clásico
C) Diente, muela, dental, dentífrico
D) Vuelo, volátil, revuelo, devoluciones
E) Portales, puerta, pórtico, portón. *
Clave: E. El lexema común a todas las palabras es port- osu variable puert-
5. La opción que presenta características del significado denotativo y
connotativo respectivamente es
A) lógico y subjetivo. * B) afectivo y lógico. C) ambiguo y social.
D) afectivo y objetivo. E) figurado y conceptual.

69. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 69
Clave: A. El significado denotativo es conocido también como significado lógico,
conceptual, cognoscitivo y está desligado del significado accesorio, contextual o
situacional. Por otro lado, el significado connotativo es subjetivo y secundario.
6. Señale la alternativa en la que se expresa significado denotativo.
A) Los productos volaron porque eran baratos.
B) Sara se moría de risa con aquellas bromas.
C) Ayer anduvimos treinta minutos por la playa.*
D) Elena era nuestro brazo derecho en la oficina.
E) No volveremos a pisar el palito nuevamente.
Clave: C. Andar involucra tiempo y espacio, por ello, se trata de significado
denotativo.
7. En el enunciado “ya viste que la niña de cinco años viste un hermoso vestido
de seda”, las palabras subrayadas están en relación semántica de
A) sinonimia.
B) cohiponimia.
C) polisemia.
D) homonimia.*
E) hiperonimia.
Clave: D. ”viste” (1), „del verbo ver‟; “viste” (2) „del verbo vestir”, presentan
coincidencias en sus formas, son de significados diferentes: evidencian la relación
de homonimia.
8. Marque la alternativa en la que se presenta polisemia.
A) Traje para ti el traje de lanilla de alpaca que tanto querías.
B) No basta que solo reconozcas que nuestra tradición es vasta.
C) Refrescó su ojo derecho con el agua del ojo del manantial.*
D) Desde el canto del balcón, su canto llega hasta nuestros oídos.
E) Después de cortar la tira de gasa, tira los hilos que no sirven.
Clave: C. Las dos palabras “ojo” están en relación de polisemia porque comparten
rasgos comunes especialmente por la forma.
9. Marque la alternativa en la que se presenta homonimia absoluta.
A) Era muy sabia: utilizaba savia de plantas para alimentarse.
B) Aquella tuna universitaria le canta a la dulce tuna peruana.*
C) El vino es de calidad, me baso en la preferencia del cliente.
D) Calle y reflexione, solo cuando salga a la calle podrá gritar.
E) Me río de la gracia de esos niños cuando nadan en ese río.
Clave: B. Las dos palabras “tuna” son sustantivos (grupo de cantantes y fruta),
luego están en relación de homonimia absoluta.

70. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 70
10. Marque la alternativa en la que se presenta homonimia parcial.
A) La manzana que crece en el huerto de esa manzana es buena.
B) Ya convine con el cocinero para que combine otros ingredientes.
C) No vote por obligación, bote ese malestar y tenga optimismo.
D) La cola para pegar es barata, haga la cola ahí para comprar.
E) Ahora cavo otra piscina en este cabo más amplio y tranquilo.*
Clave: E. Cada palabra corresponde a diferentes categorías gramaticales: la primera
es verbo (cavar); la segunda, sustantivo (porción de tierra que ingresa al mar).
11. Señale la opción que presenta significado connotativo.
A) Por su obra sobresaliente será premiado pronto.
B) El corredor participará en la competición de hoy.
C) El joven es mosca, aprovecha cada oportunidad.*
D) Está muy alegre, porque ya nació su primer hijo.
E) La abuelita de ese niño celebró su cumpleaños.
Clave: C. Expresa significado figurado: “muy mosca” para referirse metafóricamente
“muy hábil”.
12. Señale la alternativa en la que se presenta relación de sinonimia.
A) Inadecuado / inaudito B) Depreciar / devaluar*
C) Hablar / vociferar D) Suma / resta
E) Gusto /sentido
Clave: B. Entre las palabras “depreciar” y “devaluar” (disminuir el valor), hay relación
de sinonimia.
13. Señale la alternativa en la que aparecen palabras que guardan relación de
antonimia gramatical.
A) Padrino / ahijado B) Cuidado / negligencia
C) Auténtico / apócrifo D) Legal / ilegal*
E) Templado / tibio
Clave: D. La relación de antonimia se realiza mediante el uso del prefijo negativo
“i-“: se trata de antónimos gramaticales.
14. Semánticamente, las palabras color y azul son respectivamente
A) hiperónimo y cohipónimo. B) hipónimo e hiperónimo
C) cohipónimo y cohipónimo. D) homónimo y antónimo.
E) hiperónimo e hipónimo.*
Clave: E. Hay relación de hiperónimo (color, abarca más) e hipónimo (azul).

71. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 71
15. La relación semántica que existe entre las palabras negligente y eficiente es de
A) sinonimia absoluta. B) homonimia parcial.
C) antonimia complementaria.* D) homonimia absoluta.
E) antonimia recíproca.
Clave: C. Las palabras negligente y eficiente se excluyen entre sí, están en relación
de antonimia complementaria.
16. Señale la opción donde existe significado connotativo.
A) La selva peruana es bastante extensa.
B) Elvira trabaja en el laboratorio de Julia.
C) Juan, el inglés es un idioma anglosajón.
D) Ese timador no tiene sangre en la cara. *
E) Ellos se reunirán en la sala de sesiones.
Clave: D. El enunciado presenta significado secundario de “no tener sangre en la
cara”, se refiere figuradamente a „no sentir vergüenza‟.
17. Marque la alternativa en la que se presentan palabras en relación de
cohiponimia.
A) Mesa, comedor B) Copa, taza *
C) Sierra, instrumento D) Luna, satélite
E) Plata, metal
Clave: B. Las dos palabras son cohipónimos, pertenecen a la clase recipientes.
18. Señale la alternativa en la que se presenta homonimia absoluta.
A) Mundo / universo B) Ceda / seda C) Hora / ora
D) Vino / vino E) grabó /gravó *
Clave: E. Ambas palabras, “grabó” y “gravó”, son verbos. Son homónimos
absolutos.
19. En el enunciado “la tierra que guarda en un sobre le trae recuerdos de su tierra
de origen” la relación semántica entre las palabras subrayadas es de
A) homonimia parcial. B) polisemia.* C) sinonimia.
D) homonimia absoluta. E) cohiponimia.
Clave: B. El significante es uno, pero con diferentes sentidos
20. Señale la opción en la que los antónimos lexicales son recíprocos.
A) Grande / pequeño B) Tarde / noche C) Fuerte / débil
D) Abuelo / nieto* E) Correcto / errado

72. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 72
Clave: D. El término abuelo requiere de nieto; de igual modo, nieto requiere del
concepto abuelo, por ello, la relación es recíproca.
21. Marque la alternativa en la cual se presenta palabras en relación de hiponimia-
hiperonimia.
A) Coma – punto B) Sandalia-calzado * C) País – Alemania
D) Rama – árbol E) Dedo - mano
Clave: B. “Sandalia” es hipónimo de “calzado”, el hiperónimo que incluye otros tipos
de calzado.
22. En el enunciado “el caso es que ya no me caso”, la relación de significado de
las palabras subrayadas es de
A) polisemia. B) homonimia paradigmática.
C) homonimia parcial.* D) antonimia gramatical.
E) homonimia absoluta.
Clave: C. Hay homonimia parcial ya que pertenecen a categorías gramaticales
distintas: “caso” (1) sustantivo y “caso” (2) verbo, respectivamente.
23. En los espacios correspondientes, escriba la clase de relación semántica que
existe entre los pares de palabras.
A) Metal – cobre __________________________
B) Hospedar – albergar __________________________
C) Rosa – alhelí __________________________
D) Caliente – frío __________________________
E) Tres – acho __________________________
F) Veces – beses __________________________
Clave:
A) Hiperonimia B) Sinonimia
C) Cohiponimia D) Antonimia propio
E) Cohiponimia F) Homonimia parcial
24. Señale la opción que presenta significado denotativo.
A) El orador político siempre lleva agua para su molino.
B) Los payasos suelen hacer reír a todo tipo de público.
C) Su simpatía es la llave que le abre todas las puertas.
D) Cogió las flores con sus pequeñas manos de seda.
E) No se despierta, se ha quedado completamente seco.
Clave: B. El enunciado expresa significados conceptuales, lógicos.
25. Las palabras justificar y documentar se encuentran en relación de
A) antonimia. B) cohiponimia. C) sinonimia.*
D) homonimia. E) polisemia.

73. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 73
Clave: C. Justificar (Del lat. iustificāre). tr. Probar algo con razones convincentes,
testigos o documentos.
Documentar (Del lat. documentāre). tr. Probar, justificar la verdad de algo con
documentos.
26. Es una característica del significado connotativo.
A) Objetivo B) Lógico C) Ambiguo
D) conceptual E) Figurado*
Clave: E. El significado connotativo es conocido también como significado
secundario, figurado, subjetivo y está ligado al significado accesorio, contextual o
situacional.
27. Escriba pares de palabras antónimas léxicas complementarias.
A) ______________________________
B) ______________________________
C) ______________________________
Clave: A) inauguración/clausura B) correcto/errado C) auténtico/apócrifo
28. Escriba pares de palabras antónimas recíprocas.
A) ______________________________
B) ______________________________
C) ______________________________
Clave: A) deudor/acreedor B) comerciante/cliente C) jefe/subalterno
29. Escriba pares de palabras antónimas graduales
A) ______________________________
B) ______________________________
C) ______________________________
Clave:
A) malo/regular/ bueno
B) bajo/mediano/alto
C) delgado/gordo/ obeso
30. Los pares de palabras “adolescente, adulto”, “licor, vino” y “mar, lago” se
encuentran respectivamente en relación semántica de
A) cohiponimia, sinonimia y antonimia.
B) antonimia, hiponimia y sinonimia.
C) hiponimia, cohiponimia e hiperonímia.
D) antonímia, hiperonímia y cohiponimia. *
E) hiperonimia, cohiponimia y antonimia.
Clave: D)

74. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 74
31. Al especialista que elabora diccionarios se le denomina
A) semantista. B) lexicólogo. C) gramático
D) lexicógrafo*. E) escritor.
Clave: D. El lexicógrafo es el especialista que se encarga de escribir o elaborarlos
diccionarios, boletines.
32. En el enunciado “en el cáliz de oro se encuentra grabado el cáliz de una flor”,
las palabras subrayadas están en relación semántica de
A) sinonimia. B) homonimia absoluta. C) cohiponimia.
D) homonimia parcial. E) polisemia.*
Clave: E. Entre las palabras “cáliz”, hay relación de polisemia porque tienen el rasgo
común de la forma.
33. Complete las siguientes oraciones con los verbos adecuados: “verificar”,
“acreditar”, “justificar”, “documentar” o “alegar”.
A) El abogado _____________ falta de pruebas contra su patrocinado.
B) El vendedor ___________el sobreprecio con las notas de importación.
C) Esa firma será _____________ con una prueba grafotécnica.
D) Señor, tiene que ____________ su declaración de experiencia laboral.
E) ¿Cómo se puede _____________ que el personal está calificado?
Clave:
A) alega B) justifica C) verificada
D) documentar E) acreditar
34. Marque la alternativa donde hay uso adecuado del verbo “acreditar”
A) Él acredita que pronto será un buen empleado.
B) El gerente acreditará a las secretarias que faltan.
C) María está acreditando un permiso para viajar.
D) Sus eficientes obras lo acreditan como el mejor. *
E) Su mal carácter lo acredita como un antisocial.
Clave: D.
1. tr. Hacer digno de crédito algo, probar su certeza o realidad. U. t. c. prnl.
2. tr. Afamar, dar crédito o reputación. U. t. c. prnl.
3. tr. Dar seguridad de que alguien o algo es lo que representa o parece.
4. tr. Dar testimonio en documento fehaciente de que alguien lleva facultades para
desempeñar comisión o encargo diplomático, comercial, etc.
35. Escriba los antónimos gramaticales de las siguientes palabras:
A) acreditar/ ______________ E) documentado/ ______________
B) justicia/ ______________ F) democrático/ ______________
C) lealtad/ _______________ G) vulnerable/ ______________
D) crecer/ _______________ H) ordenar/ ______________

75. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 75
Claves:
A) acreditar/ desacreditar E) documentado/ indocumentado
B) justicia/ injusticia F) democrático/ antidemocrático
C) lealtad/ deslealtad G) vulnerable/ invulnerable
D) crecer/ decrecer H) ordenar/ desordenar
Literatura
SEMANA N° 8
NEOCLASICISMO ESPAÑOL (siglo XVIII)
CONTEXTO CARACTERÍSTICAS LITERARIAS REPRESENTANTES
 Llegada de
Felipe V a
Madrid en
1701.
 España
gobernada por
dinastía
borbónica
durante el siglo
XVIII.
 Francia impone
normas y
valores
literarios a toda
Europa.
 Literatura española:
continuación del clasicismo
francés del siglo XVII.
 Sentido de unidad.
Sometimiento a la autoridad
de los preceptistas.
 Expresión de lo racional que
es universal. Respeto por el
pensamiento lógico.
 Belleza y razón van de la
mano.
 Fin didáctico. Visión correcta
de la vida.
 Verosimilitud. Se rechaza la
fantasía.
1. Ensayo:
Fray Benito Jerónimo Feijoo:
Teatro crítico universal,
Cartas eruditas y curiosas.
Ignacio de Luzán: Poética.
2. Fábula:
Félix María de Samaniego:
Fábulas morales.
Tomás de Iriarte: Fábulas
literarias.
3. Teatro:
Leandro Fernández de
Moratín: El sí de las niñas.
LEANDRO FERNÁNDEZ DE MORATÍN (1760-1828)
Obras:
 Comedias: El sí de las niñas, El viejo y la niña, La mojigata, La comedia nueva o el
café
 Prosa: Los orígenes del teatro español.
SUMARIO
Literatura española de los siglos XVIII y XIX.
Neoclasicismo. Leandro Fernández de Moratín: El sí de
las niñas.
Romanticismo. Gustavo Adolfo Bécquer: Rimas y
Leyendas.

76. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 76
 Traducciones: El médico a palos, La escuela de maridos (ambas de Moliere),
Hamlet (de Shakespeare)
Características de sus obras:
 Orden, sensatez y corrección.
 Su producción teatral escrita a fines del s. XVIII y principios del s. XIX se encuadra
en el terreno de la comedia neoclásica.
 Acata la ley de las tres unidades: unidad de espacio, de tiempo y de acción.
 Su modelo constante fue Moliére, representante del clasicismo francés.
EL SÍ DE LAS NIÑAS
Referencias socioculturales:
Los personajes representan a la burguesía española. Unos, la enriquecida: don Carlos,
don Diego; otros, la empobrecida: doña Irene, doña Francisca. La obra se desarrolla en
una posada de Alcalá de Henares, una tórrida noche de verano. El clima espiritual es
opresivo debido a la actitud tiránica de una madre que obliga a su hija a contraer
matrimonio sin importarle los sentimientos de la joven.
Género: dramático, drama costumbrista.
Estilo: prosa castiza, empleando la frase corta, ágil y concisa.
Personajes: don Diego, don Carlos, doña Irene, doña Francisca, también llamada
Paquita, los criados.
Temas:
 Principal: el matrimonio concertado por los padres.
 Otros: casamiento por conveniencia, la mujer como objeto o mercancía.
Argumento
– Acto primero. Don Diego, burgués adinerado, elige como novia a doña Francisca,
una jovencita. La madre de ésta, doña Irene, apoya este ventajoso matrimonio
pretendiendo imponerse a la voluntad de su hija, quien se halla profundamente
enamorada de don Félix, joven y valiente militar.
– Acto segundo. Se descubre que don Félix es en realidad don Carlos, sobrino de
don Diego. Don Carlos llega a la posada con la intención de rescatar a su amada de
la desagradable situación, pero luego decide partir de la posada al enterarse de la
identidad del pretendiente e incluso entrevistarse con su tío -a quien respeta y
estima como a un padre-, quien le insta a regresar al cuartel y cumplir con sus
obligaciones de soldado.
– Acto tercero. Don Carlos parte de la posada, pero regresa para despedirse de su
amada. Don Diego los sorprende hablando e intercepta una carta dirigida por don
Carlos a doña Francisca, con lo que descubre la verdad sobre los sentimientos de

77. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 77
doña Francisca. Don Diego ordena que su sobrino regrese. Se cumplen así los
deseos de los enamorados, que se casarán.
ROMANTICISMO ESPAÑOL (siglo XIX)
Contexto:
 Reinado de Fernando VII.
 Influencia de las ideas liberales.
Características:
 Culto al yo. Espíritu individualista.
 Ansia de libertad.
 Angustia metafísica.
 Desconfianza de la razón; idea de lo infinito.
 Idealismo.
 Valoración de lo histórico. Se da importancia a los acontecimientos y tradiciones.
Representantes:
 Narrativa: Mariano José de Larra, Vuelva usted mañana.
 Teatro: José Zorrilla, Don Juan Tenorio.
 Poesía: José de Espronceda, El estudiante de Salamanca. Gustavo Adolfo Bécquer,
Rimas, Leyendas, Cartas desde mi celda.
GUSTAVO ADOLFO BÉCQUER (1836-1870)
Poesía: Rimas
Prosa: Leyendas, Cartas desde mi celda, Historia de los templos de España.
RIMAS LEYENDAS
Género: lírico.
Características estilísticas: poemas
breves de gran sencillez formal.
Tema: el amor idealizado.
Otros temas: la fuerza creadora del
poeta. La historia de una pasión
frustrada. El deseo amoroso. El amor
platónico. La aparición súbita del
sentimiento amoroso.
Rima IV
Fragmento:
No digáis que agotado su tesoro
de asuntos falta, enmudeció la lira;
podrá no haber poetas; pero siempre
habrá poesía.
[…]
Mientras haya unos ojos que reflejen
los ojos que los miran,
mientras responda el labio suspirando
al labio que suspira,
mientras sentirse puedan en un beso
dos almas confundidas,
mientras exista una mujer hermosa,
¡habrá poesía!
El elemento legendario y exótico aparece con
insistencia en las Leyendas de Bécquer. Destacan
las siguientes leyendas: “La ajorca de oro”, “Los
ojos verdes”, “Rayo de luna”, “Maese Pérez, el
organista”.
En “La ajorca de oro”, Bécquer hace referencia a
una hermosura diabólica, vale decir, lo bello se
mezcla con lo demoníaco. La belleza se vincula a lo
monstruoso y deforme. La hermosura es enfermiza,
e inspira vértigo y desasosiego.
“La ajorca de oro”
Fragmento:
Ella era hermosa, hermosa con esa hermosura que
inspira el vértigo, hermosa con esa hermosura que
no se parece en nada a la que soñamos en los
ángeles y que, sin embargo, es sobrenatural;
hermosura diabólica, que tal vez presta el demonio
a algunos seres para hacerlos sus instrumentos en
la tierra.
Él la amaba; la amaba con ese amor que no
conoce freno ni límite; la amaba con ese amor en
que se busca un goce y sólo se encuentran
martirios, amor que se asemeja a la felicidad y que,
no obstante, diríase que lo infunde el Cielo para la
expiación de una culpa.

78. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 78
EJERCICIOS DE CLASE
1. Son características del Neoclasicismo español, excepto
A) el sometimiento a la autoridad de los preceptistas.
B) la razón como fundamento de la formación moral.
C) la ambigüedad e imprecisión entre realidad y ficción.
D) la finalidad didáctica contenida en la obra literaria.
E) la verosimilitud opuesta al predominio de la fantasía.
Solución:
La indistinción entre realidad y ficción es una característica del Barroco español del
siglo XVII.
Clave: C
2. El Sí de las niñas se desarrolla dentro de un clima opresivo porque
A) doña Irene tiene una actitud dominante con su hijo Carlos.
B) don Diego cela constantemente a su esposa, doña Irene.
C) don Carlos es autoritario con su novia, Paquita.
D) doña Francisca se opone a los planes de su madre.
E) doña Irene obliga a su hija a contraer matrimonio.
Solución:
La obra se desenvuelve bajo un clima opresivo debido a la actitud tiránica de una
madre, doña Irene, quien impone un matrimonio concertado a su hija, sin importarle
los sentimientos de ella.
Clave: E
3. Con respecto a la verdad (V) o falsedad (F) de los siguientes enunciados sobre El sí
de las niñas, de Leandro Fernández de Moratín, marque la alternativa que contiene
la secuencia correcta.
I. Don Diego, hombre mayor, elije a una jovencita como su novia.
II. Doña Irene no comparte la idea de imponer matrimonio a los hijos.
III. Doña Francisca está sumamente enamorada de un joven militar.
IV. Don Carlos se queda en la posada y revela la verdad a su tío.
V. Al final, don Diego permite el matrimonio de Francisca y su sobrino.
A) FVFVF B) FVVFF C) FVFVV D) VFVFV E) VVFVF
Solución:
I. Don Diego, hombre entrado en años, decide casarse y elige como novia a la joven
Francisca (V). II. Don Diego es quien quiere que Francisca decida libremente porque
no comparte el criterio de imponer matrimonio a los hijos (F). III. Doña Francisca está
profundamente enamorada de un joven militar (V). IV. Don Carlos decide partir de la
posada sabiendo que pierde a su amada (F). V. Don Diego descubre el amor de los
jóvenes y decide ceder la mano de la joven a su sobrino (V).
Clave: D

79. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 79
4. “Su madre y toda la familia aplauden este casamiento. Ella (…) no ha media hora,
me ha dicho que está pronta a obedecer a su madre y darme la mano”. De este
fragmento de El sí de las niñas, se deduce que
A) los hijos deberían oponerse a sus padres.
B) el matrimonio concertado es el tema central.
C) la familia solía entrometerse en la vida ajena.
D) la madre rechazaba la mano a los pretendientes.
E) las hijas deben buscar al esposo ideal.
Solución:
En este fragmento el tema planteado es el matrimonio concertado e impuesto por los
padres.
Clave: B
5. La finalidad didáctica de El sí de las niñas radica en que el autor busca demostrar
A) los errores en la educación de las niñas.
B) la verosimilitud de los hechos representados.
C) la importancia de la madre en el matrimonio.
D) las malas relaciones entre los jóvenes enamorados.
E) que la mujer puede ser objeto de mercancía.
Solución:
La obra tiene finalidad didáctica porque el autor busca corregir los errores en la
educación de las niñas de la época, a quienes se imponía la autoridad de los
mayores quitándoles toda iniciativa sobre algo tan personal como el matrimonio.
Clave: A
6. Con respecto a las características del Romanticismo literario, marque la alternativa
que contiene el enunciado correcto.
A) Su actitud frente a la vida se sustenta en la búsqueda de lo sobrenatural.
B) Busca revalorar lo histórico a través del conocimiento y la subjetividad.
C) Expresa un marcado interés por seguir las normas y cánones sociales.
D) Representa una continuidad del neoclasicismo, ambos rechazan la fantasía.
E) Se interesa por lo sobrenatural, por lo infinito, de allí su angustia metafísica.
Solución:
Un importante rasgo romántico es la angustia metafísica, en tanto que el escritor se
interesa por lo sobrenatural, por lo que está más allá de la razón; le conmueve la
idea de lo infinito.
Clave: E
7. El idealismo romántico se expresa a través de
A) la exaltación de la propia personalidad del creador.
B) un interés desmesurado por la libertad del artista.
C) la búsqueda de un mundo superior y perfecto.
D) la desconfianza en los postulados de la razón.
E) la valoración de lo histórico y de las tradiciones.

80. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 80
Solución:
El rechazo a una realidad adversa lleva al espíritu romántico a buscar un mundo
superior que exprese los ideales que persigue.
Clave: C
8. Marque la alternativa que contiene el tema central de las Rimas, de Gustavo Adolfo
Bécquer.
A) La fuerza creadora del novelista
B) La historia de una pasión realizada
C) La superación del amor platónico
D) La existencia humana como ficción
E) El amor idealizado por el poeta
Solución:
El amor idealizado es el tema fundamental de las Rimas, de Gustavo Adolfo
Bécquer. El deseo amoroso y el amor platónico son también temas importantes.
Clave: E
9. ¿Qué tema se desarrolla en la siguiente rima de Gustavo Adolfo Bécquer?
Tú eras el huracán y yo la alta
torre que desafía su poder:
¡tenías que estrellarte o abatirme!
¡No podía ser!
A) El amor como ilusión imposible.
B) La naturaleza fuertemente exótica.
C) La lucha entre lo ideal y lo material.
D) La incomunicación entre los amantes.
E) La total idealización del ser amado.
Solución:
En la rima XLI, el tema planteado por Bécquer es el amor imposible entre la mujer y el
sujeto del poema. Imposibilidad que se refleja en las metáforas (mujer= huracán;
hombre= torre) y los paralelismos empleados por el poeta para evidenciar esa
imposibilidad.
Clave: A
10. Con respecto a la estética de lo grotesco presente en "La ajorca de oro", uno de los
relatos contenidos en Leyendas de Gustavo Adolfo Bécquer, se puede afirmar que lo
grotesco es la
A) mezcla insólita de lo diabólico y lo sublime
B) confluencia de lo monstruoso y lo enfermizo.
C) vinculación entre lo bello y lo demoníaco.
D) asociación entre la razón y la enajenación.
E) conjunción de lo angelical y lo pecaminoso.
Solución:
En "La ajorca de oro", bello relato contenido en Leyendas, de Bécquer, lo grotesco
se da en la vinculación que hace el autor entre lo bello y lo demoníaco.
Clave: C

81. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 81
Psicología
Instrucciones: Leer detenidamente cada pregunta y elegir la respuesta que se estime
verdadera.
1. La elaboración del proyecto de vida se inicia generalmente luego de un estado de
A) crisis de identidad. B) equilibrio saludable.
C) autorrealización del ser. D) autoconfianza.
E) actitud fatalista.
Solución:
La formulación del proyecto de vida se presenta luego de un periodo de crisis de
identidad, cuando el sujeto se interroga y cuestiona el sentido que debe tener su
vida
Rpta.: A
2. En el adolescente el proyecto de vida gira en torno al descubrimiento de la
A) autoestima. B) vocación. C) meta. D) estrategia. E) vivencia.
Solución:
En el adolescente el descubrimiento de la vocación es el eje central que perfila el
proyecto de vida, la cual surge como producto de una evaluación personal.
Rpta.: B
3. Cuando Bill Gates hizo referencia a “Ver un ordenador personal en cada mesa, un
ordenador que él hubiera producido", era una expresión que ilustró el contenido de
su
A) misión. B) vocación. C) visión.
D) autorrealización. E) plan.
Solución:
La visión es la imagen meta inspiradora del proyecto de vida, en este caso que todas
las personas tengan un ordenador creado por el mismo Bill Gates
Rpta.: C
4. La creatividad de un estudiante que aspira a ser arquitecto, según el análisis FODA
se constituye en una
A) oportunidad. B) amenaza. C) debilidad. D) fortaleza. E) ocasión.
Solución:
La creatividad es una aptitud un talento, es una cualidad interna de las personas que
facilita alcanzar la meta de llegar a ser un arquitecto; por tanto según el FODA es
una fortaleza
Rpta.: D

82. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 82
5. En la expresión “Tengo que ser un profesional de primer nivel dedicado a la
investigación” ilustraría fundamentalmente el concepto de
A) Visión. B) autorrealización. C) trascendencia.
D) meta. E) misión.
Solución:
La misión es una clara definición de los principios y valores (la investigación) en el
que se sustenta una persona para alcanzar su meta o visión en este caso ser un
profesional de primer nivel
Rpta.: E
6. El valor de servicio hacia los demás que anima un proyecto de vida, se le conoce
con el nombre de
A) proactividad. B) trascendencia. C) autorrealización.
D) autonomía. E) resiliencia.
Solución:
En una persona el valor de trascendencia es aquel que lo anima a aportar, contribuir
decididamente en el bienestar de los demás y de la humanidad
Rpta.: B
7. La adopción de un proyecto de vida exige a las personas que sus valores deban ser
A) auténticos. B) compartidos. C) jerarquizados.
D) justos. E) prácticos.
Solución:
Establecer un proyecto de vida implica que las personas hayan identificado y
priorizado sus valores existenciales fundamentales.
Rpta. C
8. La organización efectiva del tiempo en el proyecto de vida, obedece a un perfil de
actividades consideradas como
A) muy importante-muy urgente. B) importante-urgente.
C) no importante- urgente. D) importante-no urgente.
E) no importante-no urgente.
Solución:
El tiempo en el proyecto de vida debe estar organizado eficazmente en base a
actividades esenciales relacionados con la misión de la persona, y que estas se
deban ejecutar con anticipación; es decir actividades importantes-no urgentes
Rpta.: D
9. Actualmente es el concepto de mayor impacto en el estado de salud-enfermedad de
la población
A) Estilos de vida B) Calidad de vida C) Proyecto de vida
D) Atención médica E) Riesgo de salud

83. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 83
Solución:
Los hábitos de conducta en la alimentación, actividad física, descanso, etc. los
cuales configuran un estilo de vida se ha constituido en el factor explicativo de
mayor incidencia en el binomio salud- morbilidad.
Rpta.: A
10. En la prevención del abuso sexual a los niños se debe incentivar en ellos el valor
y respeto de su
A) familia. B) obediencia. C) sexo. D) habilidad. E) cuerpo.
Solución: La educación del niño sobre el respeto y valor de su cuerpo, desterrando el
castigo y el maltrato constituye una medida preventiva contra el abuso sexual.
Rpta.: E
Historia
1. En qué contexto histórico fue creado el virreinato del Perú.
A) Durante la resistencia en Vilcabamba de Túpac Amaru I contra al virrey Toledo.
B) Cuando Hernández Girón fue derrotado por el ejército de la Real Audiencia.
C) Después que fue derrotado Gonzalo Pizarro por el Pacificador Pedro de La Gasca.
D) Tras la victoria del comisionado Cristóbal Vaca de Castro sobre Almagro el Mozo.
E) Cuando Manco Inca iniciaba en el Cuzco la resistencia contra Francisco Pizarro.
Rpta: “D”. El virreinato del Perú fue creado por Real Cédula promulgada por el rey
de España Carlos V, en noviembre de 1542, dos meses después de la batalla de
Chupas (16 de setiembre de 1542), cuando el comisionado Cristóbal Vaca de Castro
vencía al ejército de Almagro el Mozo.
2. Una de las atribuciones políticas de la Real Audiencia consistió en
A) actuar como máximo tribunal comercial para todos los virreinatos.
B) asesorar al virrey y reemplazarlo en caso se produjese la vacancia.
C) proponer al rey el nombramiento de todas las autoridades virreinales.
D) realizar el juicio de residencia al virrey cuando culminaba su gobierno.
E) elaborar reales cédulas para su promulgación por parte de los oidores.
Rpta: B. Una de las funciones de la Real Audiencia fue actuar como tribunal judicial
para solucionar litigios entre españoles. Pero en el campo político asesoraban al
virrey y lo reemplazaban en caso de vacancia.
3. Papel que cumplió el gobernador de Panamá Pedro de los Ríos durante los viajes
realizados por los conquistadores.
A) Apoyó a los conquistadores en su búsqueda del imperio de los incas.
B) Impulsó las exploraciones de Pascual de Andagoya hacia el Amazonas.
C) Se opuso a las exploraciones llevadas a cabo por Pizarro y Almagro.
D) Aprobó los acuerdos alcanzados por Pizarro con los Reyes Católicos.
E) Alentó la firma con la corona Española de la Capitulación de Toledo.

84. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 84
Rpta: C. El gobernador de Panamá Pedro de los Ríos ajustició a Pedro Arias Dávila.
Cuando se enteró del cuarteto enviado dentro de un ovillo de algodón por el soldado
Juan de Saravia, comprendió que el viaje de Pizarro era un abuso contra la
soldadesca española, envió por ello al comisionado Juan Tafur para obligarlos a
regresar.
4. El acuerdo principal del Tratado de Acobamba firmado por Tito Cusi Yupanqui con
las autoridades españolas fue
A) permitir el ingreso de misioneros a Vilcabamba.
B) aceptar el vasallaje con el rey de España Carlos V.
C) apoyar la política real de extirpación de idolatrías.
D) oponerse al movimiento religioso del Taky Onkoy.
E) impulsar el establecimiento de la Santa Inquisición.
Rpta: A. El Tratado de Acobamba firmado en Apurímac entre Tito Cusi Yupanqui y
las autoridades españolas, suscribía como acuerdo principal el permitir a los
misioneros tener acceso a Vilcabamba a cambio de la oferta de paz por parte de los
españoles.
5. El virrey Blasco Nuñez de Vela se enfrentó a los rebeldes liderados por Gonzalo
Pizarro con la finalidad de
A) eliminar definitivamente todas las encomiendas indianas.
B) reconocer el dominio sobre el Cuzco por Diego de Almagro.
C) entregar encomiendas a los incas de Vilcabamba en el Cuzco.
D) defender a los indios del abuso de los corregidores y caciques.
E) establecer las Leyes Nuevas que afectaba a los encomenderos.
Rpta: E. La guerra entre el virrey Blasco Núñez de Vela y el líder de los
encomenderos Gonzalo Pizarro tuvo como finalidad establecer las Leyes Nuevas en
el virreinato del Perú que afectaba a los encomenderos.
Educación Cívica
EJERCICIOS N° 8
1. Problema de convivencia democrática en el Perú, en el que participan funcionarios
públicos para obtener un beneficio ilícito.
A) Corrupción B) Crimen organizado
C) Delincuencia financiera D) Discriminación laboral
E) Xenofobia urbana
Solución:
La corrupción es uno de los principales problemas de convivencia, por ello es
considerado una lacra social que se expresa por el hecho de realizar un pago ilegal
por un servicio o un favor deshonesto por parte de un trabajador público.
Clave: A

85. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 85
2. Las normas jurídicas, han sido establecidas por el Estado con el propósito de
___________ las conductas dentro de la sociedad al margen de consideraciones
políticas, económicas y sociales.
A) sostener B) imponer C) modificar
D) regular E) renovar
Solución:
Las normas jurídicas, han sido establecidas por el Estado con el propósito de regular
la interrelación entre los hombres y de estos con el Estado.
Clave: D
3. Colocar verdadero (V) o falso (F) en referencia a la convivencia democrática.
1.- Las normas morales son reglas de conducta colectiva. ( )
2.- La delincuencia se encuentra en descenso en el Perú. ( )
3.- La corrupción es una lacra social. ( )
4.- La discriminación vulnera el derecho a la igualdad. ( )
A) V–F–F–V B) V–F–V– V C)F–F–V–V
D) V–V–F–V E) V–F–V– F
Solución:
La secuencia correcta es F – F – V – V. Las normas morales son reglas de conducta de
carácter interno; la delincuencia de bandas organizadas se expande por todas las
regiones. La corrupción es una lacra social. La discriminación vulnera el derecho a la
igualdad.
Clave: C
4. La _________ es un conjunto de valores, actitudes y comportamientos que rechazan
la violencia y previenen los conflictos promocionando los derechos humanos.
A) convivencia democrática B) cultura de paz
C) mediación pactada D) diversidad social
E) negociación interétnica
Solución:
La cultura de paz es el conjunto de valores, actitudes, tradiciones, comportamientos
y estilos de vida basados en el respeto a la vida, el fin de la violencia, la promoción y
la práctica de la no violencia. El desarrollo pleno de una cultura de paz está
íntegramente vinculado a la promoción de la democracia y el desarrollo pleno de los
derechos humanos.
Clave: B
5. Conjunto de personas que comparten nacionalidad, religión, lengua o tradiciones
culturales.
A) Estado B) Gobierno C) Etnia
D) Comunidad E) Asentamiento

86. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 86
Solución:
El término etnia comprende los factores culturales nacionalidad, afiliación tribal,
religiosa, fe, lengua, o tradiciones; y biológicos de un grupo humano.
Clave: C
6. En referencia a la diversidad lingüística peruana, es correcto afirmar que
A) el jaqaru es lengua predominante en el altiplano.
B) existen 16 lenguas en todo el Perú.
C) las lenguas nativas predominan en la selva.
D) la lengua más hablada es la machiguenga.
E) el Perú conserva más de 150 lenguas.
Solución:
Las lenguas nativas se hablan, sobre todo, en los Andes centrales y en la selva
amazónica. Un número considerable de las lenguas septentrionales andinas se
hablaban en la costa norte y los Andes septentrionales, pero se extinguieron.
Las únicas lenguas nativas andinas en actual uso son el quechua y el aymara, el
jaqaru y el kawki se encuentran en extinción (prov. de Yauyos); mientras que la
región amazónica alberga una mayor variedad de lenguas, siendo las lenguas más
habladas el asháninca y el aguaruna. Actualmente se ha definido 16 familias
lingüísticas en el territorio peruano. El Estado peruano (que impuso el español)
redujeron el número de lenguas indígenas a menos de 70 en la actualidad.
Clave: C
7. Es el conjunto de vestigios materiales, heredados de la época colonial y republicana,
y que forman parte de nuestra identidad y nuestro acervo cultural.
A) Santuario natural B) Santuario histórico
C) Patrimonio arqueológico D) Patrimonio histórico
E) Patrimonio natural
Solución:
De acuerdo con el Ministerio de Cultura, el Patrimonio Histórico es parte integrante
del Patrimonio Cultural, conformado por el patrimonio mueble e inmueble de las
épocas colonial y republicana que forman parte del Patrimonio Cultural de la nación.
Clave: D
8. La revaloración de las manifestaciones folklóricas autóctonas y las que surgieron
como consecuencia del mestizaje, se define como
A) cultura de paz. B) desarrollo equilibrado. C) integración social.
D) identidad cultural. E) fragmentación cultural.
Solución:
Forjar la identidad cultural es revalorar las manifestaciones folklóricas autóctonas y
las que surgieron como consecuencia del mestizaje, practicándolas y difundiéndolas
en toda la nación sin ninguna discriminación.
Clave: D

87. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 87
9. La fortaleza del Real Felipe y las iglesias coloniales son consideradas
A) patrimonio arqueológico. B) patrimonio histórico inmueble.
C) patrimonio arqueológico mueble. D) zonas arqueológicas.
E) reserva histórica.
Solución:
La fortaleza de Real Felipe y las iglesias coloniales son consideradas, patrimonio
histórico mueble que corresponde desde las épocas colonial y republicana y forman
parte del Patrimonio Cultural de la Nación.
Clave: B
10. Es un método de resolución de conflictos, en el cual, la actuación de un tercero
imparcial, ayuda a las partes en disputa a dialogar sobre sus intereses y encontrar
una solución en forma cooperativa.
A) La mediación B) La conciliación C) La jurisprudencia
D) La negociación E) La prebenda
Solución:
Mediación en Derecho, es un método de resolución de conflictos mediante la
actuación de un tercero imparcial que ayuda a las partes en disputa, a dialogar sobre
sus intereses y encontrar una solución en forma cooperativa. Es uno de los métodos
más utilizados en disputas: familiares, comerciales, comunitarias e incluso
internacionales. El mediador no tiene poder de decisión sobre la disputa, sino que
aplica técnicas y estrategias de diálogo y cooperación, ayudando tanto a la solución
como a la mejora de las relaciones interpersonales o institucionales de los
disputantes. Actualmente, la mediación permite resolver cuestiones sin recurrir a la
violencia o a la demanda judicial.
Clave: A
Economía
1. Si hay un aumento de la demanda de autos entonces los precios
A) disminuyen. B) permanecen. C) compiten.
D) suben. E) concuerdan.
“D” Según la ley de la oferta y la demanda a mayor demanda mayor precio.
2. Las medicinas poseen una demanda
A) equilibrada. B) inelástica. C) elástica.
D) unitaria. E) favorable.
“B” En tanto que las medicinas son productos de primera necesidad el alza de sus
precios no altera su demanda.
3. Dado el caso que aumenta el precio de la energía eléctrica entonces su demanda
A) varia. B) es unitaria. C) resiste.
D) retrocede. E) es inelástica.

88. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 88
“E” En el caso de la demanda inelástica, una variación del precio no trae como
consecuencia una variación drástica de la demanda.
4. En un modelo de mercado de competencia perfecta los vendedores y los
compradores tienen igual
A) poder. B) precio. C) tecnología.
D) oportunidad. E) calidad.
“D” En un mercado de competencia perfecta los vendedores y los compradores
tienen igual oportunidad para vender o comprar sus productos.
5. En un mercado de competencia imperfecta, los precios son determinados por el
A) gobierno. B) intermediario. C) inversionista.
D) mercado. E) vendedor.
“E” El mercado imperfecto es monopólico como por lo tanto un vendedor o varios
fijan los precios.
6. En el/la __________________ existen barreras técnicas y legales rígidas para el
ingreso de nuevos productores al mercado.
A) competencia perfecta B) monopolio C) oligopolio
D) competencia monopolística E) libre competencia
“B” Los monopolios imponen una serie de cortapisas para el ingreso de nuevos
vendedores.
7. Las transnacionales, ejercen prácticas monopólicas puesto que
A) influyen poco sobre el precio.
B) invierten grandes sumas en publicidad.
C) liberan la entrada al mercado.
D) existe pocos vendedores o compradores.
E) producto difícil de sustituir.
“B” Las transnacionales se caracterizan por invertir ingentes cantidades de dinero
en publicidad.
8. Son una clase de sociedades monopólicas cuyo objetivo es apropiarse de la mayoría
de acciones de otras empresas para manipularlas.
A) trust B) consorcio C) holding
D) cartel E) conglomerado
“C” El holding busca capturar el máximo de acciones de otras empresas para
manipularlas.

89. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 89
9. Si un grupo de empresas textiles acuerda dividir el mercado para evitar competir
entre ellas, están constituyendo un
A) conglomerado. B) consorcio. C) cartel.
D) holding. E) trust.
“C” El cartel, que esta conformado por empresas de la misma rama productiva,
acuerdan precios y volúmenes de producción para manipular el mercado.
10. El oligopolio se caracteriza porque existen pocos
A) accionistas. B) servicios. C) bancos.
D) operadores. E) productores.
“E” El oligopolio es un tipo de mercado donde existen pocos productores a la vez
que una gran cantidad de consumidores.
Biología
EJERCICIOS DE CLASE Nº 08
1. Es una fitohormona que estimula el crecimiento de la planta actuando a nivel de la
pared celular y estimulando la división celular.
A) Auxina B) Citocinina C) Giberelina
D) Ácido abscísico E) Etileno
Rpta. “A” La auxina es una hormona que promueve la elongación de las células en
los coleóptilos y en otras zonas de brote.
2. La hormona que ayuda a las plantas a resistir condiciones ambientales
desfavorables se denomina
A) citosina. B) auxina. C) giberelina.
D) etileno. E) ácido abscísico.
Rpta. “E” El Ácido abscísico hace que se cierren los estomas cuando hay poca
disponibilidad de agua. Inhibe la actividad de la giberelina, con lo que conserva el
estado de latencia de las yemas y de las semillas en tiempos en los que sería
peligrosa la germinación.
3. En el sistema endocrino, las hormonas deben actuar sobre _________________
para iniciar su reacción.
A) células de defensa B) glóbulos blancos C) glóbulos rojos
D) células blanco E) plaquetas
Rpta. “D” La especificidad de una hormona está determinada por receptores
localizados sobre las células blanco; si una célula carece del receptor específico
para una hormona, ésta no actuará sobre ella.

90. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 90
4. Las hormonas _______________, se unen a receptores que se encuentran en la
membrana de la célula blanco.
A) proteicas B) esteroideas C) animales
D) vegetales E) polipeptídicas
Rpta. “A” Las hormonas proteicas se unen a un receptor presente en la membrana
de las células blanco, esto induce la producción de una sustancia llamada segundo
mensajero que tiene un efecto específico dentro de la célula.
5. Uno de los principales órganos blanco de la hormona folículo estimulante es
A) el hígado. B) el hipotálamo. C) la tiroides.
D) la hipófisis. E) el ovario.
Rpta. “E” La FSH estimula células en el ovario, que en las mujeres estimula el
crecimiento del folículo y la secreción de estrógenos. En los varones estimula la
espermatogénesis.
6. ¿Cómo se denomina la hormona hipofisiaria que estimula la secreción de las
glándulas mamarias?
A) Luteinizante B) Folículo estimulante C) Oxitocina
D) Del crecimiento E) Adrenocorticotrópica
Rpta. “C” La oxitocina, en conjunto con otras hormonas, estimula el desarrollo de
las glándulas mamarias durante el embarazo. La succión realizada por el recién
nacido estimula la liberación de la oxitocina, la cual a su vez estimula la secreción de
leche.
7. Si los niveles de calcio llegan a ser muy elevados en la sangre, ________________
liberará____________
A) la tiroides – tiroxina. B) la tiroides – calcitonina.
C) el páncreas – insulina. D) la paratiroides – paratohormona.
E) el testículo – testosterona.
Rpta. “B” Si los niveles de calcio llegan a ser muy elevados en la sangre, la
glándula tiroides liberará calcitonina, la cual inhibe la liberación de calcio a partir de
los huesos.
8. Es una hormona que combate el estrés aumentando la concentración de glucosa en
sangre y la velocidad de formación de glucógeno en el hígado.
A) Epinefrina B) Antidiurética C) Oxitocina
D) Cortisol E) Aldosterona
Rpta. “D” El cortisol es una hormona que combate el estrés aumentando la
concentración de glucosa en la sangre y la velocidad de formación de glucógeno en
el hígado.

91. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 91
9. La hormona ___________________liberada desde la hipófisis posterior, evita
deshidratación.
A) antidiurética B) oxitocina C) epinefrina
D) aldosterona E) tiroxina
Rpta. “A” La hormona antidiurética ocasiona que mucha más agua se reabsorba de
la orina y sea retenida en el cuerpo, al incrementar la permeabilidad al agua de los
túbulos colectores de los nefrones del riñón.
10. La hormona que eleva la concentración sanguínea de glucosa se denomina
A) glucagón. B) aldosterona. C) insulina.
D) testosterona. E) calcitonina.
Rpta. “A” El glucagón activa una enzima hepática que convierte el glucógeno en
glucosa, elevando las concentraciones sanguíneas de glucosa.
11. Son células presentadoras de antígenos, que permiten la activación de los linfocitos.
A) Fagocitos B) Linfocitos C) Macrófagos
D) Osteocitos E) Leucocitos
Rpta. “C” Los macrófagos alteran a los antígenos haciendo que la respuesta
inmune de los linfocitos sea más eficaz.
12. Los linfocitos T y B tienen la capacidad de _____________, de modo que si la
exposición al antígeno es repetida se puede producir su rápida destrucción.
A) inhibir B) suprimir C) cooperar
D) asesinar E) recordar
Rpta. “E” Los linfocitos T y B tienen la capacidad de recordar, de modo que si la
exposición es repetida se puede producir la destrucción rápida del antígeno.
13. Son las proteínas encargadas de unirse al complejo antígeno-anticuerpo, facilitando
la fagocitosis.
A) Del complemento B) Citoquinas C) Monoquinas
D) Lactasas E) Proteasas
Rpta. “A” Las proteínas del complemento son las encargadas de unirse al complejo
antígeno-anticuerpo facilitando la fagocitosis o la lisis de las células infectadas.
14. Si el sistema inmunológico no está autorregulado se pueden producir enfermedades
de tipo autoinmunes. De la lista marque la que NO corresponde a este grupo.
A) Vitíligo B) Lupus eritematoso C) Polio
D) Psoriasis E) Artritis reumatoidea

92. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 92
Rpta. “C” Si el sistema inmunológico no está autoregulado se pueden producir
enfermedades inmunopatológicas, a excepción de la polio.
15. La inmunidad pasiva ______________, se produce cuando los anticuerpos pasan de
la madre al feto.
A) vectorial B) artificial C) atenuada D) natural E) selectiva
Rpta. “D” La inmunidad pasiva natural se produce cuando los anticuerpos pasan de
la madre al feto o a través de la leche materna al recién nacido.
Física
EJERCICIOS DE CLASE N° 8
(ÁREAS A, D y E)
1. Se eleva un bloque de 10 kg de masa desde el reposo, con aceleración constante de
magnitud 3 m/s2
, durante 5 s. ¿Cuál es su energía cinética al cabo de ese tiempo?
A) 950 J B) 1 125 J C) 1 570 J D) 1230 J E) 1080 J
Solución:
s/m15)5)(3(tataVV 0 
J2511)15(10
2
1
E
)at(m
2
1
Vm
2
1
E
2
C
22
C


Clave: B
2. Una lámpara, de masa 2 kg se desprende desde una altura de 3 m y cae sobre el piso.
¿Cuál es la energía cinética de la lámpara cuando llega al piso?
(g = 10 m/s2
)
A) 45 J B) 60 J C) 120 J D) 90 J E) 180 J
H
F
a
F

93. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 93
A
B
r =2m
r =2m
r =1m
Solución:
Hg2VVm
2
1
mgHEE 22
cgp 
J60Hgm)Hg2(m
2
1
Vm
2
1
E 2
C 
Clave: B
3. En la figura, el trabajo total realizado sobre el bloque de masa 2 kg entre los puntos A y B
es 64 J. Determine la energía cinética del bloque en el punto B.
A) 75 J
B) 90 J
C) 100 J
D) 125 J
E) 150 J
Solución:
J100)6)(2(
2
1
J64E
mV
2
1
WE:entonces,Vm
2
1
EEW
2
)B(c
2
A)B(C
2
A)B(C


Clave: C
4. Determine la rapidez en el punto B, cuando la bolita de peso 0,5 N se desplaza desde el
punto A con rapidez inicial 5 m/s hacia el punto B. Se desprecia todo tipo de rozamiento.
A) 10 m/s
B) 15 m/s
C) 9 m/s
D) 7 m/s
E) 5 m/s
6m
V = 6m/sA VB
A B

94. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 94
F(N)
x(m)
20
10
0 5 10
m
F
Solución:
  s/m5VV
2
1
5
2
1
)1(10
Vm
2
1
Vm
2
1
mgH
)B(E)A(E
B
2
B
2
2
B
2
AA
MM



Clave: E
5. La figura muestra un bloque que parte del reposo en la posición A y se desplaza a lo largo
de la superficie lisa ABC. Determinar la distancia BC recorrida por el móvil al detenerse en
la posición C. Considerar 1,0 en el plano BC.
(g = 10 m/s2
)
A) 20 cm
B) 10 cm
C) 15 cm
D) 25 cm
E) 12 cm
Solución:
m10
1,0
1
dluegodgmVm
2
1
0
W)M(E)M(E
2
B
BC fc


Clave: B
6. La figura muestra la gráfica de la fuerza horizontal F en función de la posición x. La fuerza F
actúa sobre un bloque que se encuentra sobre una superficie lisa. Calcular el trabajo
realizado por la fuerza desde x = 0 hasta x = 10 m.
A) 55 J
B) 100 J
C) 120 J
D) 165 J
E) 150 J
H=1m
C B
A
d
=0

95. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 95
10cm
H
Solución:
J100)m10()N20(
2
1
Wárea 
Clave: B
7. El trabajo efectuado por una fuerza al estirar 20 cm un resorte es 9,0 J. ¿Qué energía
potencial elástica tendrá el resorte, al estirarlo 10 cm?
A) 2, 25 J B) 6, 0 J C) 4, 5 J D) 3, 0 J E) 9, 0 J
Solución:
J25,2J10x225E
)10x10()450(
2
1
E:luego
m/N450k)10x20(
2
1
9xk
2
1
W
2
c
22
222
ep






Clave: B
8. La figura muestra un resorte de constante elástica K = 300 N/m comprimido 10 cm y a una
esfera de masa 150 g ubicado en su extremo libre. Calcular la altura H máxima,
que alcanza la esfera cuando abandona el resorte. (Despreciar el rozamiento).
A) 0,5 m
B) 1 m
C) 1,5 m
D) 2 m
E) 3 m
Solución:
m1
30
30
15
30
2
1
10x15
3
2
1
H
N10x1510x10x15
s
m
10xkg10x150mg
3)10(x300xk
m10m10x10cm10x
1
123
2
3
12
12























Clave: B

96. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 96
H
F
a
F
V = 0m/s0
F(N)
x(m)
20
10
0 5 10
m
F
EJERCICIOS DE CLASE N° 8
(ÁREAS B, C y F)
1. Se eleva un cuerpo de 1 kg de masa, con una aceleración de 3 m/s2
, durante 5 s. ¿Cuál es
su energía cinética al cabo de ese tiempo?
A) 225 J B) 112, 5 J C) 56,25 J D) 85 J E) 170 J
Solución:
s/m15)5)(3(tataVV 0 
J5,112)15)(1(
2
1
)at(m
2
1
Vm
2
1
E
2
22
C


Clave: B
2. La figura muestra la gráfica de la fuerza horizontal F en función de la posición x. La fuerza F
actúa sobre un bloque que se encuentra sobre una superficie lisa. Calcular el trabajo
realizado por la fuerza desde x = 0 hasta x = 10 m.
A) 55 J
B) 100 J
C) 120 J
D) 165 J
E) 150 J
Solución:
J100)m10()N20(
2
1
Wárea 
Clave: B

97. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 97
C B
A
H=1m
3. La figura muestra un bloque que parte del reposo en la posición A y se desplaza a lo largo
de la superficie lisa ABC. Calcular la rapidez en el punto C.
(g = 10 m/s2
)
A) m5
B) m52
C) m55
D) 7 m
E) 4 m
Solución:
m52Hg2V:entonces,Vm
2
1
Hgm
)M(E)M(E
C
2
C
CA


Clave: B
4. En la figura, el trabajo total realizado sobre el bloque de masa 2 kg entre los puntos A y B
es 64 J. Determine la energía cinética del bloque en el punto B.
A) 75 J
B) 90 J
C) 100 J
D) 125 J
E) 150 J
Solución:
J100
)6)(2(
2
1
J64
mV
2
1
WE:entonces,Vm
2
1
EEW
2
2
A)B(C
2
A)B(CC



Clave: C
6m
V = 6m/sA VB
A B

98. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 98
F
K
5. En la figura mediante la fuerza F se estira lentamente el resorte de constante elástica K =
200 N/m. Calcular la energía potencial elástica cuando el resorte se ha estirado 10 cm.
A) 3 J
B) 1 J
C) 2 J
D) 2,5 J
E) 0,5 J
Solución:
J1)10(100W
)10x10()200(
2
1
W
xK
2
1
W
2
22
2





Clave: B
Química
AREAS: A – D- E
SEMANA N°8: CONCEPTO DE MOL – ESTEQUIOMETRIA Y CÁLCULOS
ESTEQUIOMÉTRICOS
1. Indique la equivalencia correcta
A) Un mol de plata : 6,02x1023
moléculas de Ag.
B) Una mol de agua : 6,02x1023
unidades fórmulas de H2O.
C) Una mol de cloruro de sodio : 6,02x1023
moléculas de NaCℓ.
E) Una mol de ozono : 1,80x1024
átomos de O.
D) Una mol de oxígeno a CN : 44,8 L de O2
Solución:
A) Una mol de plata : 6,02x1023
átomos de Ag.
B) Una mol de agua : 6,02x1023
moléculas de H2O
D) Una mol de cloruro de sodio : 6,02x1023
unidades fórmulas de NaCℓ
C) Una mol de ozono : 1,80x1024
átomos de O
E) Una mol de oxígeno a CN : 22,4 L de O2
Rpta. D

99. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 99
2. La epsomita, ampliamente usada en agricultura y jardinería, es el sulfato de
magnesio heptahidratado. Determine el peso fórmula del compuesto.
Pesos Atómicos: Mg = 24 S = 32 O = 16 H=1
A) 246 B) 264 C) 323 D) 236 E) 228
Solución:
Fórmula química = MgSO4. 7H2O
Peso Fórmula: 24 + 32 + 4(16) + 7 (18) = 246
Rpta. A
3. ¿Cuántos iones Mg2+
y moléculas de agua están presentes en 2,46 g de epsomita?
A) 6,0 x 1020
y 4,2 x 1021
B) 1,2 x 1020
y 4,2 x 1020
C) 6,0 x 1021
y 2,4 x 1022
D) 3,0 x 1020
y 4,2 x 1021
E) 6,0 x 1021
y 4,2 x 1022
Solución:







 221
24
223
24 Mgiones10x6,0
OH.7MgSOg246
Mgiones10x6,0
OH.7MgSOg2,46
O
O
2
22
24
2
23
24 Hmoléculas10x4,2
OH7.MgSOg246
Hmoléculas10x6,0x7
OH.7MgSO 





g2,46
Rpta. E
4. Determine la fórmula molecular de un compuesto orgánico, cuyos datos son:
A) C3H8O B) C2H20O C) C2H4O2 D) C2H3O2 E) C2H5O2
Solución:
Elemento Peso ÷ Peso atómico(u) = n n
 2
30
60
CH
PM
OHC
PM
2
zyx
O
C2H4O2 = CH3COOH
C 40,0 ÷ 12 = 3,33 3,33 ÷ 3,33 = 1
H 6,7 ÷ 1 = 6,7 6,7÷3,33 = 2
O 53,3 ÷ 16 = 3,33 3,33 ÷ 3,33 = 1
Rpta. C
Elemento % Peso Peso atómico(u)
C 40,0 12
H 6,7 1
O 53,3 16
PM CxHyOz = 60

100. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 100
5. Los metales del grupo IA, reaccionan violentamente con el agua formando los
respectivos hidróxidos y liberando hidrógeno gaseoso. Si 4,6 g de sodio reaccionan
con suficiente cantidad de agua, ¿Cuántos gramos de su respectiva base se forman?
P.At. Na = 23
A) 2,0 B) 2,5 C) 3,0 D) 4,0 E) 6,5
Solución:
2 Na(s) + 2 H2O(l)  2 NaOH(ac) + H2(g) + Q
NaOHg4,0
Nag23x2
NaOHg40x2
Nag2,3 





Rpta. D
6. Determine las moles de la sal oxisal formada y el volumen en L, medidos a CN del
gas liberado, si se descomponen térmicamente 840 g de bicarbonato de sodio:
NaHCO3(s) + Q  Na2CO3(s) + CO2(g) + H2O(v)
PF NaHCO3 = 84
A) 6 y 112 B) 5 y 112 C) 6 y 224 D) 5 y 114 E) 6 y 336
Solución:
Balanceando:
2 NaHCO3(s) + Q  Na2CO3(s) + CO2(g) + H2O(v)
32
3
2
3
2
CONademoles5
NaHCOg84x2
Namol1
NaHCOg10x8,4 




 3CO
2
CN3
3
2
COdeL112
NaHCOg84x2
L22,4
NaHCOg10x8,4 




 2CO
Rpta. B
7. Quince TM de coque de 80% de pureza arde en presencia de aire. Determine las
moléculas de CO2 generadas a través de la reacción de síntesis si se sabe que el
rendimiento de la reacción es del 90%.
A) 6,0 x 1029
B) 5,4 x 1028
C) 4,5 x 1029
D) 6,0 x 1028
E) 5,4 x 1029
Solución:

101. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 101
2
292
236
COmoléculas10x6
Cg12
COmoléculas10x06,
CTM1
C10
coqueTM100
CTM80
coqueTM15 
















 g
Aplicando Rendimiento:
2
29
2
2
2
29
COmoléculas10x5,4
COmoléculas
COmoléculas90
COmoléculas10x6 





100
Rpta. E
8. Determine los gramos de agua formada cuando 44,8 L de oxígeno gaseoso medidos
a CN, reaccionan con 12 g de hidrógeno gaseoso, ¿cuántas moles del reactivo en
exceso queda sin reaccionar?
A) 72 g H2O y 1 mol H2 B) 72 g H2O y 1 mol O2
C) 36 g H2O y 2 mol H2 D) 72 g H2O y 2 mol H2
E) 72 g H2O y 2 mol O2
Solución:
O2(g) + 2 H2(g)  2 H2O(l)
2 moles O2 = 44,8 L O2 (CN)
6 moles H2 = 12 g H2
Entonces:
1 mol O2 reacciona con 2 moles de H2
2 moles de O2 reaccionarán con 4 moles de H2, por tanto quedan 2 moles de H2 sin
reacionar
O
1
O
2
2
2
2 Hg72
Omol
Hg18x2
Omoles2 





Rpta. D
9. Si se combinan 16 g de metano con 32 g de oxígeno a partir de la reacción:
CH4(g) + 2 O2(g)  CO2(g) + 2 H2O(v) + Q
La secuencia correcta de verdad (V) o falsedad (F) es:
I. El reactivo limitante es el metano.
II. Quedan sin reaccionar 8 g de Oxígeno.
III. Se generan 1,2 moles de gases considerando un rendimiento del 80%.
A) VFF B) FVV C) FFV D) VVF E) VFF
Solución:
I. FALSO: El reactivo limitante es el O2.
1 mol CH4 (16 g) requiere 2 moles de O2(64 g)  O2 es reactivo limitante.
II. FALSO: Quedan sin reaccionar 8 g de CH4.

102. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 102
III. VERDADERO: Se generan 1,2 moles de gases considerando un rendimiento
del 80%
CH4(g) + 2 O2(g)  CO2(g) + 2 H2O(v) + Q
32 g O2 reacciona con 8 g de CH4 y genera 0,5 mol de CO2 y y mol de H2O
totalizando 1,5 moles de gas, aplicando el 80% de rendimiento se generaría:
1,5 moles x 0,8 = 1,2 moles de gases de combustión
Rpta. C
EJERCICIOS DE REFORZAMIENTO
1. Determine el Nº de átomos de H contenidos en 344 g de yeso: CaSO4.2H2O
PF CaSO4.2H2O = 172
A) 2,4 x 1023
B) 4,4 x 1024
C) 4,8 x 1024
D) 2,4 x 1024
E) 4,8x1023
Solución:
H.átomos10x4,8
O2HCaSOg
Hátomos10x6,0x4
O2HCaSOg344 24
24
23
24 





172
Rpta. C
2. En 4 unidades fórmula (UF) de FeCℓ3 hay……………………………….. iones Cℓ1–
A) 1,2 x 101
B) 7,2 x 1024
C) 7,2 x 1023
D) 7,2 x 101
E) 2,4 x 101
Solución:
-124
3
-123
3 Ciones10x7,2
FeC1
Ciones10x6,0x3
FeCUF4 


 





UF
Rpta. B
3. Determine el % de pureza del KCℓO3, si se sabe que en la descomposición de 245 g
del reactivo se obtuvo 44,8 L de oxígeno, medidos a CN.
2KCℓO3(s) + Q   2MnO
2 KCℓ (s) + 3 O2(g)
PF KCℓO3 = 122,5
A) 80,0 B) 75,5 C) 95,0 D) 66,7 E) 85,5
Solución:
2 KCℓO3(s) + Q  2 KCℓ (s) + 3 O2(g)
3
2
3
2 OKCg163,33
OL22,4x3
OKCg5,1222
OL44,8 






 x
 pureza%66,7100x
OKCg245
OKCg163,33
3
3








Rpta. D

103. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 103
4. ¿Cuál fue el rendimiento de la reacción, si se obtuvieron 50 g de NaCℓ a partir de 23
g de sodio y 71 g de cloro gaseoso?
PF NaCℓ = 58,5 P.At. Na = 23 P.At. Cℓ = 35,5
A) 80,0 B) 75,5 C) 95,0 D) 90,5 E) 85,5
Solución:
2 Na(s) + Cℓ2(g)  2 NaCℓ (s)
23 g Na = 1 mol Na 71 g Cℓ2 = 1 mol Cℓ2
Reactivo Limitante = Na


NaCg58,5
Nag232
NaCg58,5x2
Nag23 





x
 oRendimient%85,5100x
NaCg58,5
NaCg50








Rpta. E
AREAS B – C – F
SEMANA N°8: CONCEPTO DE MOL – ESTEQUIOMETRIA Y CÁLCULOS
ESTEQUIOMÉTRICOS
1. Con respecto al concepto de mol marque la secuencia correcta.
I. En una mol de H2(g) hay 6,02x1023
moléculas de hidrógeno.
II. En 18 g de H2O hay una mol y contiene 6,02x1023
moléculas de H2O.
III. Una mol de oxígeno a CN ocupa 44,8 L y tiene una masa de 32g.
IV. En una mol de moléculas de ozono(O3) hay 1,80x1024
átomos de O.
A) VFVF B) FVVF C) FFVV D) VVFV E) VFFV
Solución:
I. VERDADERO: En una mol de H2(g) hay 6,02x1023
moléculas de hidrógeno.
II. VERDADERO: En 18 g de H2O hay una mol y contiene 6,02x1023
moléculas de
H2O.
III. FALSO: Una mol de oxígeno a CN ocupa 44,8 L y tiene una masa de 32g.
IV. VERDADERO: En una mol de moléculas de ozono(O3)hay1,80x1024
átomosde O.
Rpta. D
2. Determine el peso fórmula del MgSO4.7H2O (sulfato de magnesio heptahidratado).
Pesos Atómicos: Mg = 24 S = 32 O = 16 H=1
A) 246 B) 264 C) 323 D) 236 E) 228
Solución:

104. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 104
Fórmula química = MgSO4. 7H2O
Peso Fórmula: 24 + 32 + 4(16) + 7 (18) = 246
Rpta. A
3. El sodio reacciona violentamente con el agua de acuerdo a la siguiente reacción:
Na(s) + H2O(l)  NaOH(ac) + H2(g) + Q
Si 4,6 g de sodio reaccionan con suficiente cantidad de agua, ¿Cuántos gramos de
de hidróxido y moles de H2(g) se forman?
P.At. Na = 23
A) 2,0 y 0,50 B) 2,5 y 0,20 C) 3,0 y 1,00
D) 4,0 y 0,05 E) 6,0 y 0,05
Solución:
Ecuación balanceada
2 Na(s) + 2 H2O(l)  2 NaOH(ac) + H2(g) + Q
NaOHg4,0
Nag23x2
NaOHg40x2
Nag2,3 





2
2
Hdemoles0,05
Nag23x2
Hdemol1






Nag2,3
4. Si se combinan 16 g de metano con 32 g de oxígeno a partir de la reacción:
CH4(g) + 2O2(g)  CO2(g) + 2 H2O(v) + Q
La secuencia correcta de verdad (V) o falsedad(F) es:
Datos: CH4 = 16 O = 16
I. El reactivo limitante es el metano.
II. Quedan sin reaccionar 8 g de Oxígeno.
III. Se forman 1 moles de agua.
A) VFF B) FVV C) FFV D) VVF E) VFF
Solución:
I. FALSO: El reactivo limitante es el O2.
1 mol CH4 (16 g) requiere 2 moles de O2(64 g)  O2 es reactivo limitante.
II. FALSO: Quedan sin reaccionar 8 g de CH4.
III. VERDADERO: Se generan 1 mol de gases agua
CH4(g) + 2 O2(g)  CO2(g) + 2 H2O(v) + Q

105. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 105
32 g O2 reacciona con 8 g de CH4 y genera 0,5 mol de CO2 y mol de H2O
Rpta. C
EJERCICIOS DE REFORZAMIENTO
1. Determine el Nº de átomos de H contenidos en 36 g de H2O
H2O = 18 H = 1
A) 2,4 x 1023
B) 4,4 x 1024
C) 4,8 x 1024
D) 2,4 x 1024
E) 4,8x1023
Solución:
H.átomos10x2,4
OH1
Hdeátomos2
OHg18
OHdemoléculas10x6,0
OHg36 24
22
2
23
2 











demolécula
Rpta. D
2. En 4 moles de NH3 hay……. gramos y …..………moléculas de NH3
A) 17 y 6,0 x 1023
B) 68 y 1,2 x 1024
C) 56 y 2,4 x 1024
D) 68 y 2,4 x 1024
E) 82 y 6,0 x 1023
Solución:
NHdeg68
NHmoles1
g17
NHmoles4 3
3
3 





3
24
3
3
23
3 NH10x2,4
NHmoles1
NH10x6,0
NHmoles4 moléculas
moléculas






Rpta. D
3. Determine los gramos de agua formada cuando 44,8 L de oxígeno gaseoso medidos
a CN, reaccionan con 12 g de hidrógeno gaseoso, ¿cuántas moles del reactivo en
exceso queda sin reaccionar?
A) 72 g H2O y 1 mol H2 B) 72 g H2O y 1 mol O2
C) 36 g H2O y 2 mol H2 D) 72 g H2O y 2 mol H2
E) 72 g H2O y 2 mol O2
Solución:
O2(g) + 2 H2(g)  2 H2O(l)
2 moles O2 = 44,8 L O2 (CN)
6 moles H2 = 12 g H2
Entonces:

106. UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I
Solucionario de la semana Nº 8 Pág. 106
1 mol O2 reacciona con 2 moles de H2
2 moles de O2 reaccionarán con 4 moles de H2, por tanto quedan 2 moles de H2 sin
reacionar
O
1
O
2
2
2
2 Hg72
Omol
Hg18x2
Omoles2 





Rpta. D