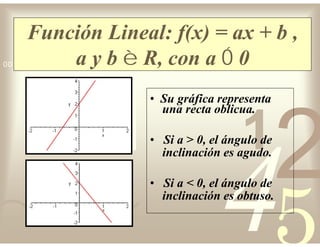
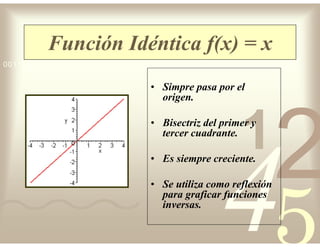
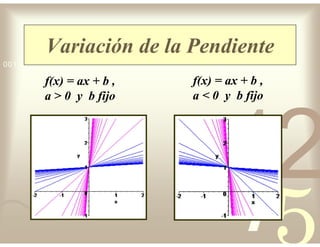
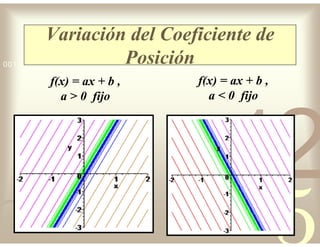
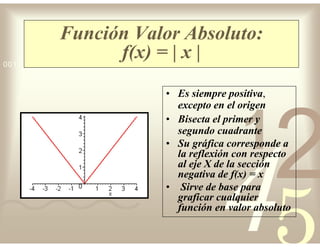
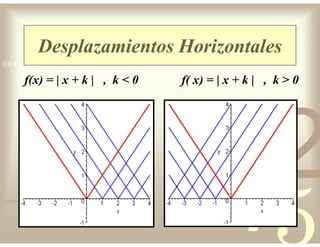
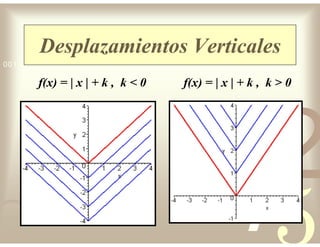
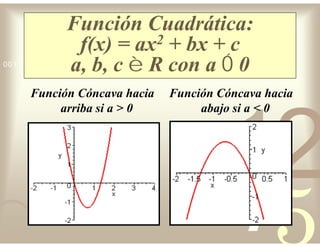
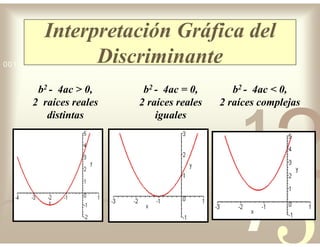
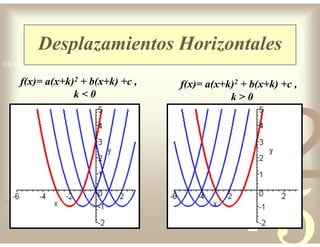
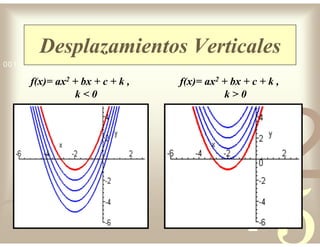
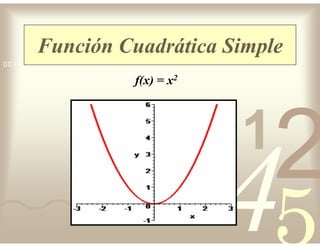
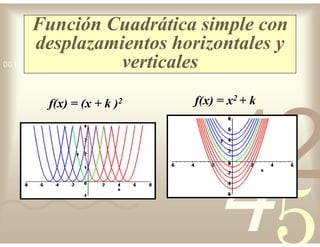
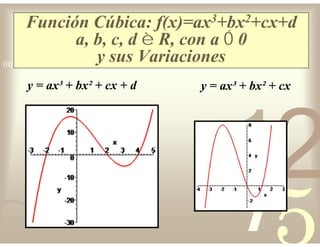
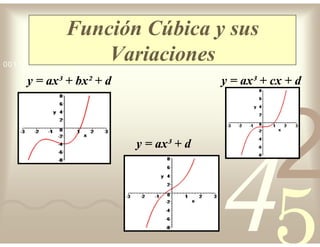
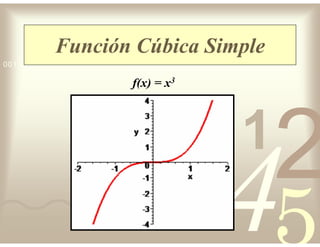
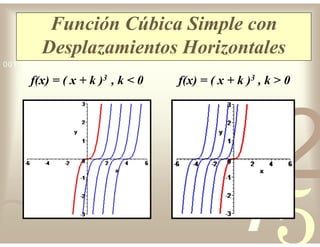
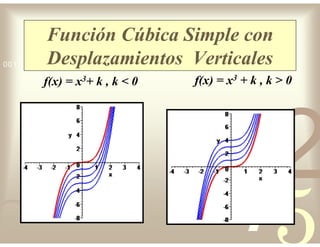
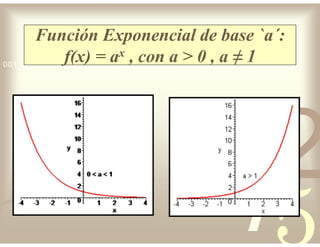
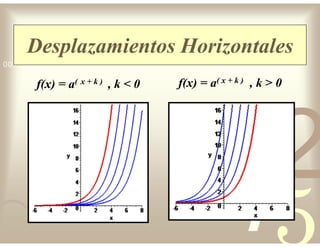
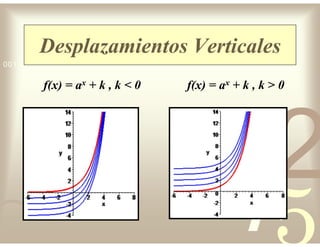
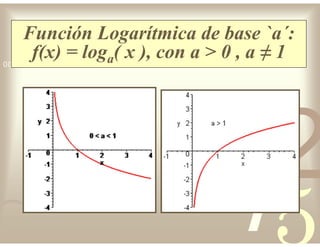
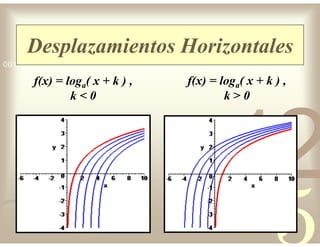
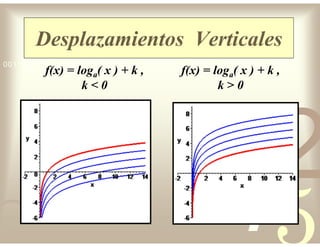
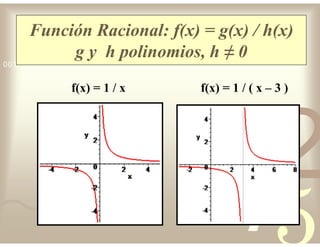
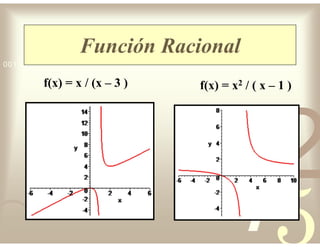
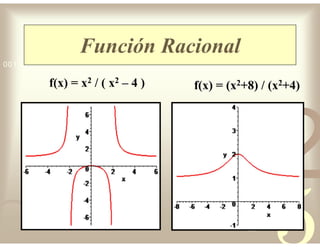
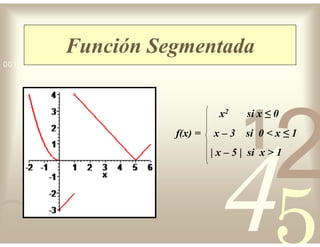
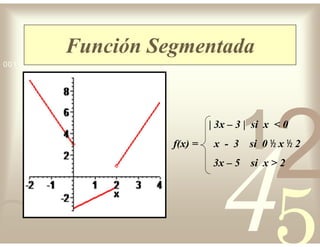
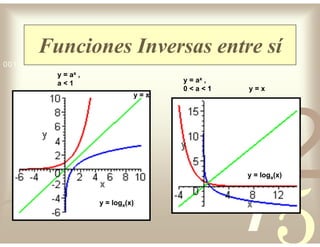
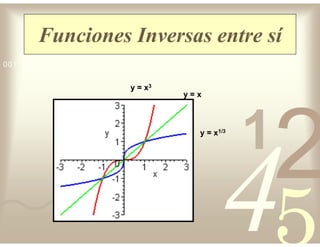
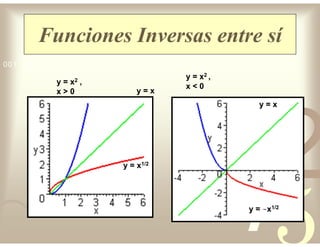
Este documento describe diferentes tipos de funciones reales de variable real, incluyendo funciones constantes, lineales, cuadráticas, cúbicas, exponenciales, logarítmicas y racionales. Explica sus características gráficas y cómo se ven afectadas por desplazamientos horizontales y verticales. También cubre funciones segmentadas e inversas entre sí.

1. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Tipos de Funciones
Reales de Variable
Real
Ing. Luis David Narváez

2. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Constante: f(x) = k ,
k  R
• Si k > 0, su gráfica se
ubica por sobre el eje X.
• Si k = 0, su gráfica se
ubica en el eje X.
• Si k < 0, su gráfica se
ubica bajo el eje X.

3. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Lineal: f(x) = ax + b ,
a y b  R, con a  0
• Su gráfica representa
una recta oblicua.
• Si a > 0, el ángulo de
inclinación es agudo.
• Si a < 0, el ángulo de
inclinación es obtuso.

4. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Idéntica f(x) = x
• Simpre pasa por el
origen.
• Bisectriz del primer y
tercer cuadrante.
• Es siempre creciente.
• Se utiliza como reflexión
para graficar funciones
inversas.

5. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Variación de la Pendiente
f(x) = ax + b ,
a > 0 y b fijo
f(x) = ax + b ,
a < 0 y b fijo

6. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Variación del Coeficiente de
Posición
f(x) = ax + b ,
a > 0 fijo
f(x) = ax + b ,
a < 0 fijo

7. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Valor Absoluto:
f(x) = | x |
• Es siempre positiva,
excepto en el origen
• Bisecta el primer y
segundo cuadrante
• Su gráfica corresponde a
la reflexión con respecto
al eje X de la sección
negativa de f(x) = x
• Sirve de base para
graficar cualquier
función en valor absoluto

8. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Desplazamientos Horizontales
f(x) = | x + k | , k < 0 f( x) = | x + k | , k > 0

9. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Desplazamientos Verticales
f(x) = | x | + k , k < 0 f(x) = | x | + k , k > 0

10. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Cuadrática:
f(x) = ax2 + bx + c
a, b, c  R con a  0
Función Cóncava hacia
arriba si a > 0
Función Cóncava hacia
abajo si a < 0

11. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Interpretación Gráfica del
Discriminante
b2 - 4ac > 0,
2 raíces reales
distintas
b2 - 4ac = 0,
2 raíces reales
iguales
b2 - 4ac < 0,
2 raíces complejas

12. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Desplazamientos Horizontales
f(x)= a(x+k)2 + b(x+k) +c ,
k < 0
f(x)= a(x+k)2 + b(x+k) +c ,
k > 0

13. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Desplazamientos Verticales
f(x)= ax2 + bx + c + k ,
k < 0
f(x)= ax2 + bx + c + k ,
k > 0

14. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Cuadrática Simple
f(x) = x2

15. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Cuadrática simple con
desplazamientos horizontales y
verticales
f(x) = (x + k )2 f(x) = x2 + k

16. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Cúbica: f(x)=ax3+bx2+cx+d
a, b, c, d  R, con a  0
y sus Variaciones
y = ax³ + bx² + cx + d y = ax³ + bx² + cx

17. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Cúbica y sus
Variaciones
y = ax³ + bx² + d y = ax³ + cx + d
y = ax³ + d

18. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Cúbica Simple
f(x) = x3

19. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Cúbica Simple con
Desplazamientos Horizontales
f(x) = ( x + k )3 , k < 0 f(x) = ( x + k )3 , k > 0

20. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Cúbica Simple con
Desplazamientos Verticales
f(x) = x3+ k , k < 0 f(x) = x3 + k , k > 0

21. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Exponencial de base `a´:
f(x) = ax , con a > 0 , a ≠ 1

22. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Desplazamientos Horizontales
f(x) = a( x + k ) , k < 0 f(x) = a( x + k ) , k > 0

23. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Desplazamientos Verticales
f(x) = ax + k , k < 0 f(x) = ax + k , k > 0

24. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Logarítmica de base `a´:
f(x) = loga( x ), con a > 0 , a ≠ 1

25. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Desplazamientos Horizontales
f(x) = loga( x + k ) ,
k < 0
f(x) = loga( x + k ) ,
k > 0

26. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Desplazamientos Verticales
f(x) = loga( x ) + k ,
k < 0
f(x) = loga( x ) + k ,
k > 0

27. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Racional: f(x) = g(x) / h(x)
g y h polinomios, h ≠ 0
f(x) = 1 / x f(x) = 1 / ( x – 3 )

28. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Racional
f(x) = x / (x – 3 ) f(x) = x2 / ( x – 1 )

29. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Racional
f(x) = x2 / ( x2 – 4 ) f(x) = (x2+8) / (x2+4)

30. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Segmentada
x2 si x ≤ 0
f(x) = x – 3 si 0 < x ≤ 1
| x – 5 | si x > 1

31. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Función Segmentada
| 3x – 3 | si x < 0
f(x) = x - 3 si 0  x  2
3x – 5 si x > 2

32. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Funciones Inversas entre sí
y = ax ,
a < 1
y = x
y = loga(x)
y = ax ,
0 < a < 1 y = x
y = loga(x)

33. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Funciones Inversas entre sí
y = x3
y = x
y = x1/3

34. 42
5
1
0011 0010 1010 1101 0001 0100 1011
Funciones Inversas entre sí
y = x2 ,
x > 0 y = x
y = x1/2
y = x2 ,
x < 0
y = x
y = x1/2