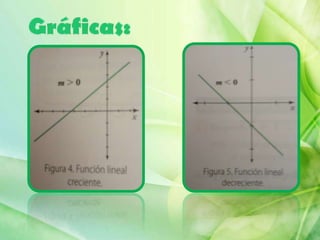
Este documento describe diferentes tipos de funciones, incluyendo funciones lineales, cuadráticas, cúbicas, exponenciales y logarítmicas. Explica sus dominios, rangos y propiedades gráficas como pendiente, vértice y simetría. También define las funciones inversas y cómo determinarlas a partir de la función original.

1. Según las propiedades que
cumplen.
Según el tipo de
ecuación, veamos…

2. # reales constantes
Función de variable real.

3.  El Dominio y el Rango, es el conjunto de # reales.
Su gráfica es una recta en el plano cartesiano.
Si m es # real + , Crece.
Si m es # real − , Decrece.
Si m es 0 , Constante.
Para determinar su gráfica, vasta con conocer 2 puntos del plano cartesiano que
satisfagan la ecuación de la función.
Para calcular la pendiente: m= Y2 − Y1 , donde X1, X2, Y1, Y2 son coordenadas de los puntos
X2 − X 1 (X1, Y1) y (X2,Y2 ), respectivamente.
El valor de b es el punto de corte de la gráfica, con el eje Y, y o intercepto.
Para determinar la ecuación de la función, se tiene en cuenta que la pendiente es la
misma sin importar qué puntos se estén considerando. Por tanto, la función es:
Y − Y1 = m(X − X1), así, Y= m(X − X1) +Y1 ó Y = m(X − X2) +Y2.

6. a, b, c # reales.
a≠0.
Función de variable real.

7. Su gráfica es una parábola.
 Abre hacia arriba si a > 0.
 Abre hacia abajo si a < 0.
 La función es par si b = 0, o sea es simétrica respecto al eje Y.
Las coordenadas del vértice v se representan (h, k) y se determinan
mediante las expresiones h = −b y k = f (− b )
2a 2a
La ecuación de su eje de simetría es x = h.
El dominio de una función cuadrática es el conjunto de los números
reales y el rango se determina a partir de su ecuación o su representación
grafica. Por tanto, si a > 0, entonces , Ran f = * k, ∞); mientras que si a < 0,
entonces , Ran f = [− ∞, k).

10. 3 2
a, b, c ,d son # reales
a≠0
Variable real.

11.  Tiene como dominio y como rango al conjunto de los # reales.
A partir de la grafica es posible determinar si la función es creciente, decreciente,
impar, o los puntos de corte de la grafica con los ejes coordenados.
No todas la funciones cúbicas tienen las mismas propiedades y características.
Si la ecuación cubica es de la forma f(x) = ax 3 , se puede concluir que la función es
impar, por lo cual es simétrica con respecto al origen. Además, la función es creciente
en todo su dominio y el punto de corte con el eje X y con el eje Y se da en el punto
(0,0).

12. Función cúbica que tiene 2 puntos de corte en el eje X, no es creciente ni
decreciente en todo su dominio y tampoco es una función impar.
f(x) = ax 3+bx 2 f(x) = ax 3+bx 2

13. Función cúbica decreciente en todo su dominio.

14. 2 funciones cúbicas, las cuales a pesar de tener la misma fórmula general, no tienen
gráficas con la misma característica.
Creciente en todo su Tiene regiones donde es
dominio. creciente y otras en donde es
decreciente, no es ni par ni impar.

15. x
a # real positivo ≠ 1
Variable real
El valor de a es constante y se
conoce como base de la función.
X es la variable independiente.

16. Dom f = R y Ran f = R+ , pues ninguna potencia de a toma valores negativos y nunca
es = 0. Además, la función f(x)= ax es inyectiva.
La gráfica de la función exponencial es creciente cuando a > 1, y es decreciente
cuando 0 < a < 1.
La gráfica de una función exponencial pasa por el punto (0,1) ya que a 0=1.

19. y
a =y
f(x) =LogaX Expresión
algebraica
a # real positivo ≠ 1
Log a X = y
Es el exponente al cual debe
elevarse a para obtener x
Variable real.

20. Dom f = R +y Ran f = R . Además, la función f(x) = Log a x
La gráfica es creciente cuando a > 1, y es decreciente cuando 0 < a < 1.
La gráfica pasa por los puntos (1,0) y (a,1), pues Log a 1 = 0, y Log a a = 1.

22. Sea f una función inyectiva, se define la función inversa f -1
cuyo dominio es Ran f y cuyo rango es Dom f, f -1 =(y) = x
si y solo si y = f (x), para todo y E Ran f

23. Devuelve a la imagen Y en su preimagen X. por esto la función debe ser uno a uno, de
lo contrario se estaría devolviendo a la imagen en 2 preimagenes, lo cual no cumpliría
con la definición de función.
La tabla, presenta los datos de la función descrita en el diagrama
sagital y de su inversa.

24. Para determinar la Inversa de una Función a partir de su
expresión algebraica:
 1. Verificar que la función sea inyectiva.
 2. Escribir la función de la forma y = f (x).
 3. Expresar X en términos de Y.
 4. Intercambiar las variables X y Y, para obtener la expresión algebraica que
representa a la función inversa.

25. La gráfica de una función inversa Y = -1 (x), obtiene al reflejar la gráfica de f
f se
respecto de la recta Y = x