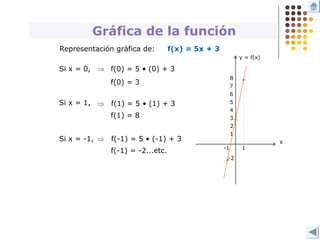
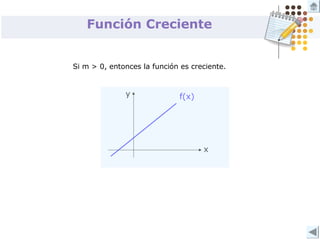
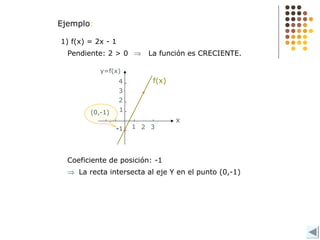
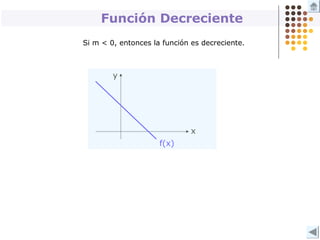
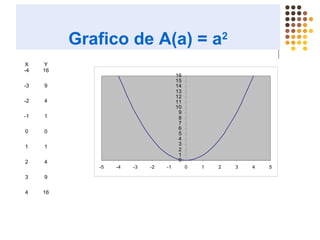
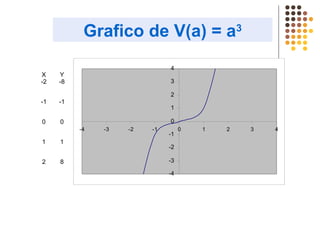
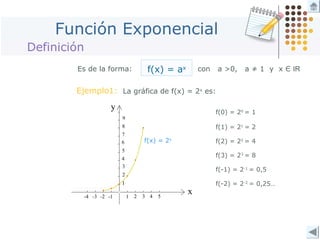
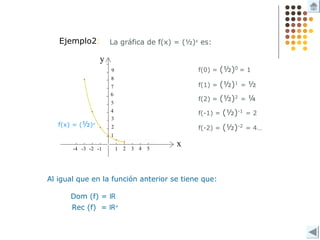
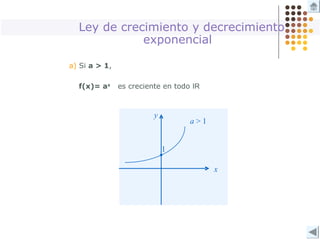
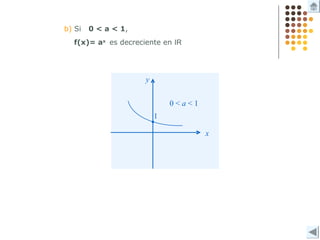
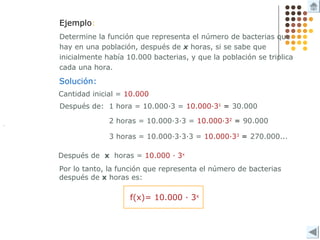
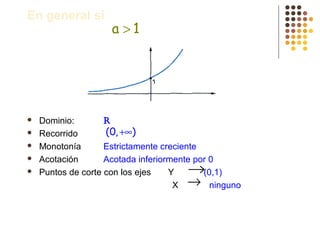
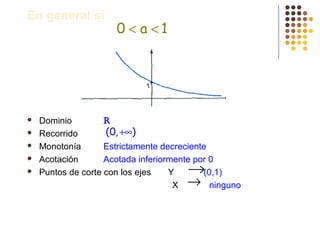
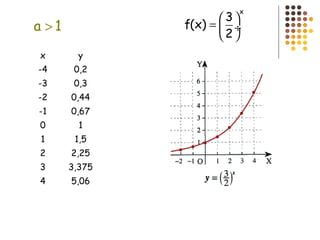
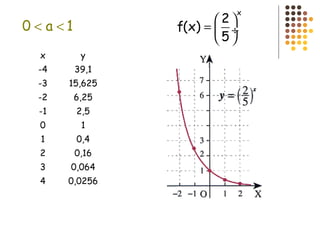
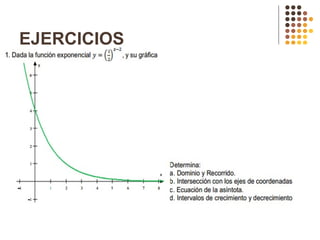
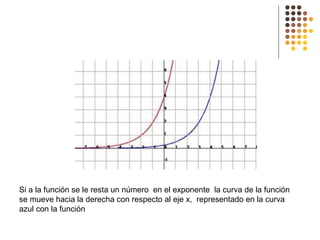
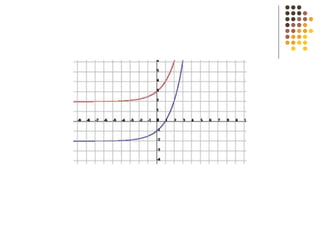
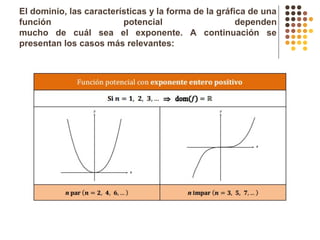
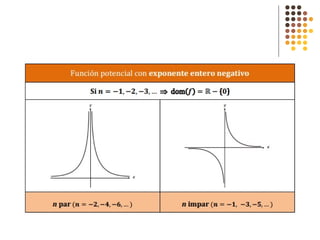
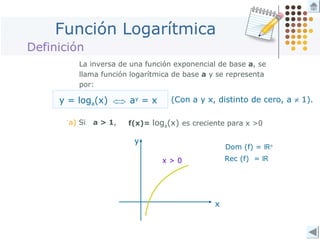
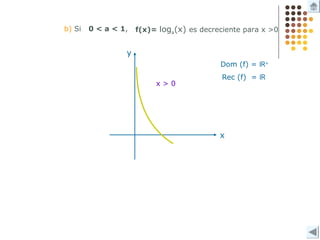
Este documento describe diferentes tipos de funciones como funciones lineales, potenciales, exponenciales y logarítmicas. Explica cómo analizar el comportamiento gráfico y analítico de estas funciones, incluyendo su pendiente, dominio, recorrido y si son crecientes o decrecientes. También incluye ejemplos y gráficos para ilustrar cada tipo de función.

1. Función
exponencial y
potencia
Miss Yanira Castro Lizana

2. Aprendizajes esperados:
• Analizan el comportamiento gráfico y
analítico de las funciones potencia,
logarítmica y exponencial.

3. Objetivo:
• Analizar el comportamiento gráfico y
analítico de las función Potencia.

4. f(x) = mx + n
m: pendiente
n : coeficiente de posición
Ejemplo:
En la función: f(x) = 5x + 3
Pendiente (m)= 5
Coeficiente de posición (n)= 3
Indica el punto donde la
recta intersecta al eje Y
La línea recta: La recta está representada por:
Repaso de las Funciones

5. Representación gráfica de: f(x) = 5x + 3
Si x = 0,
f(0) = 3
Si x = 1,
f(1) = 8
Si x = -1,
f(-1) = -2...etc.
⇒
⇒
⇒
f(0) = 5 • (0) + 3
f(1) = 5 • (1) + 3
f(-1) = 5 • (-1) + 3
Gráfica de la función

6. Si m > 0, entonces la función es creciente.
x
y f(x)
Función Creciente

7. Ejemplo:
1) f(x) = 2x - 1
Pendiente: 2 > 0 La función es CRECIENTE.
-1 1 2 3
3
1
2
4
y=f(x)
x
Coeficiente de posición: -1
La recta intersecta al eje Y en el punto (0,-1)
⇒
⇒
(0,-1)
f(x)

8. Si m < 0, entonces la función es decreciente.
x
y
f(x)
Función Decreciente

9. 1 2 3
3
1
2
4
-1
x
y= f(x)
Ejemplo:
1) f(x) = -5x + 4
Pendiente: -5 < 0 La función es DECRECIENTE.
Coeficiente de posición: 4
La recta intersecta al eje Y en el punto (0,4)
⇒
⇒
(0,4)
Siempre el dominio y el recorrido de las funciones de la forma
f(x) = mx + n, es el conjunto IR.

10. Función Constante
Si m = 0, entonces la función es constante y es de la forma:
x
y
f(x)
La representación gráfica de una función constante es una
línea recta, paralela al eje x:
f(x) = c Donde c número real

11. 1 2 3
3
1
2
4
-1
y = f(x)
x
f(x) = 3
Pendiente: 0 La función es CONSTANTE.
Ejemplo:
Coeficiente de posición: 3
La recta intersecta al eje Y en el punto (0,3)
⇒
⇒
f(x)
(0,3)

12. Función Potencia
Ejemplo: Expresar el área de la cara de un cubo y su volumen en
términos de la arista; construir una tabla de valores, el
gráfico de la función correspondiente y determinar los
valores posibles que puede tomar la variable independiente.
arista (a)
Área = a2
Volumen = a3
⇒ A(a) = a2
⇒ V(a) = a3
Es de la forma: f(x) = axn
.

13. Grafico de A(a) = a2
X
-4
Y
16
-3 9
-2 4
-1 1
0 0
1 1
2 4
3 9
4 16
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
-5 -4 -3 -2 -1 0 1 2 3 4 5

14. Grafico de V(a) = a3
X
-2
Y
-8
-1 -1
0 0
1 1
2 8
-4
-3
-2
-1
0
1
2
3
4
-4 -3 -2 -1 0 1 2 3 4

15. Función Exponencial
Es de la forma: f(x) = ax con a >0, a ≠ 1 y x Є IR
Definición
Ejemplo1:
f(x) = 2x
f(0) = 20
= 1
f(1) = 21
= 2
f(2) = 22
= 4
f(3) = 23
= 8
f(-1) = 2-1
= 0,5
f(-2) = 2-2
= 0,25…
La gráfica de f(x) = 2x
es:

16. Ejemplo2:
f(x) = (½)x
f(0) = (½)0
= 1
La gráfica de f(x) = (½)x
es:
f(1) = (½)1
= ½
f(2) = (½)2
= ¼
f(-1) = (½)-1
= 2
f(-2) = (½)-2
= 4…
Dom (f) = IR
Rec (f) = IR+
Al igual que en la función anterior se tiene que:

17. Ley de crecimiento y decrecimiento
exponencial
a) Si a > 1,
f(x)= ax
es creciente en todo IR
x
y
a > 1
1

18. b) Si 0 < a < 1,
f(x)= ax
es decreciente en IR
x
y
0 < a < 1
1

19. Ejemplo:
Determine la función que representa el número de bacterias que
hay en una población, después de x horas, si se sabe que
inicialmente había 10.000 bacterias, y que la población se triplica
cada una hora.
Solución:
Por lo tanto, la función que representa el número de bacterias
después de x horas es:
.
Cantidad inicial = 10.000
Después de: 1 hora = 10.000·3 = 10.000·31
= 30.000
2 horas = 10.000·3·3 = 10.000·32
= 90.000
3 horas = 10.000·3·3·3 = 10.000·33
= 270.000...
Después de x horas = 10.000 · 3x
.
f(x)= 10.000 · 3x

20. En general si
 Dominio: R
 Recorrido
 Monotonía Estrictamente creciente
 Acotación Acotada inferiormente por 0
 Puntos de corte con los ejes Y (0,1)
X ninguno
a 1>
(0, )+∞
→
→

21. En general si
 Dominio R
 Recorrido
 Monotonía Estrictamente decreciente
 Acotación Acotada inferiormente por 0
 Puntos de corte con los ejes Y (0,1)
X ninguno
0 a 1< <
(0, )+∞
→
→

22. x y
-4 0,2
-3 0,3
-2 0,44
-1 0,67
0 1
1 1,5
2 2,25
3 3,375
4 5,06
a 1>
x
3
f(x)
2
 
=  ÷
 

23. x y
-4 39,1
-3 15,625
-2 6,25
-1 2,5
0 1
1 0,4
2 0,16
3 0,064
4 0,0256
0 a 1< <
x
2
f(x)
5
 
=  ÷
 

24. EJERCICIOS

27. Traslaciones Función Exponencial
 La función exponencial tiene como fórmula
general f(x)= ax
, con a real positivo
distinto de 1.
 Si realizamos una suma o una resta en el
exponente la curva de la función expresa un
movimiento horizontal con respecto al eje x.
 Si a la función se le suma un número en el
exponente la curva de la función se mueve
hacia la izquierda con respecto al eje x,
representado en la curva roja con la función .

28. Si a la función se le resta un número en el exponente la curva de la función
se mueve hacia la derecha con respecto al eje x, representado en la curva
azul con la función

29.  De otra forma si nosotros sumamos o
restamos a la función en si obtenemos una
traslación vertical con respecto al eje y.
 - Si a la función se le suma un número
la curva de la función se mueve hacia arriba
con respecto al eje y, representado en la
curva roja con la función .
 - Si a la función se le resta un número
la curva de la función se mueve hacia a
abajo con respecto al eje y, representado en
la curva azul con la función .

31. Función Potencial
 Una función potencial es una función de la
forma:

En donde el exponente n es un número real
fijo.
El dominio, las características y la forma de la
gráfica de una función potencial dependen
mucho de cuál sea el exponente.

32. El dominio, las características y la forma de la gráfica de una
función potencial dependen
mucho de cuál sea el exponente. A continuación se
presentan los casos más relevantes:

36. Función Logarítmica
Definición
La inversa de una función exponencial de base a, se
llama función logarítmica de base a y se representa
por:
.
y = loga(x) ay
= x
a) Si a > 1, f(x)= loga(x) es creciente para x >0
x
y
x > 0
(Con a y x, distinto de cero, a ≠ 1).
Rec (f) = IR
Dom (f) = IR+

37. b) Si 0 < a < 1, f(x)= loga(x) es decreciente para x >0
x
y
x > 0
Dom (f) = IR+
Rec (f) = IR