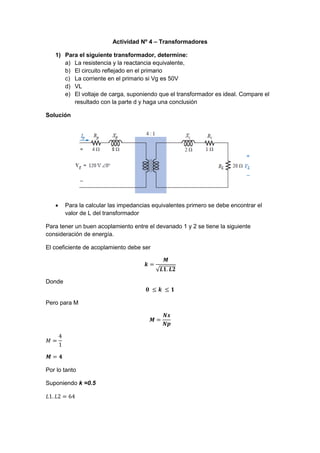
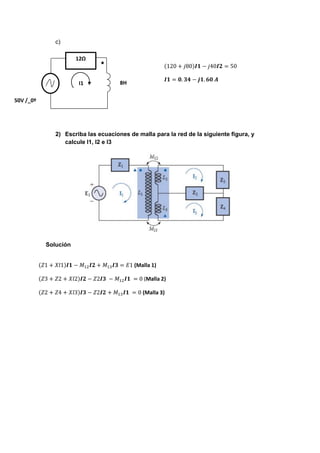
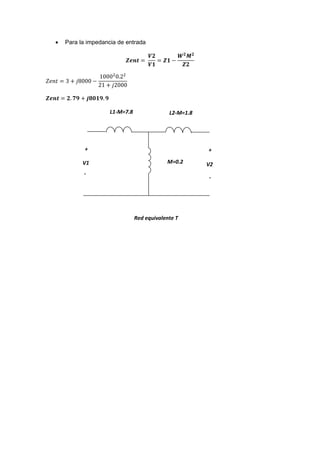
1) Se calculan las impedancias equivalentes del transformador como 80Ω. El circuito reflejado en el primario consiste en una resistencia de 12Ω en serie con una reactancia de 80Ω. La corriente en el primario sería de 0.5-j1.8A con una tensión VL de 11.5-j41.4V. 2) Se escriben las ecuaciones de malla para calcular las corrientes I1, I2 e I3 en el circuito dado. 3) La impedancia de entrada del transformador es 2.79+j8019.

1. UNIVERSIDAD FERMIN TORO
VICE RECTORADO ACADEMICO
FACULTAD DE INGENIERIA
CABUDARE EDO – LARA
Actividad No. 4
Wilfredo González
Ci.: 23.495.375
Sección: SAIA B
Prof.: Matilde García
Circuitos Eléctricos II
Cabudare, 17 de Julio de 2016

2. Actividad Nº 4 – Transformadores
1) Para el siguiente transformador, determine:
a) La resistencia y la reactancia equivalente,
b) El circuito reflejado en el primario
c) La corriente en el primario si Vg es 50V
d) VL
e) El voltaje de carga, suponiendo que el transformador es ideal. Compare el
resultado con la parte d y haga una conclusión
Solución
 Para la calcular las impedancias equivalentes primero se debe encontrar el
valor de L del transformador
Para tener un buen acoplamiento entre el devanado 1 y 2 se tiene la siguiente
consideración de energía.
El coeficiente de acoplamiento debe ser
𝒌 =
𝑴
√𝑳𝟏. 𝑳𝟐
Donde
𝟎 ≤ 𝒌 ≤ 𝟏
Pero para M
𝑴 =
𝑵𝒔
𝑵𝒑
𝑀 =
4
1
𝑴 = 𝟒
Por lo tanto
Suponiendo k =0.5
𝐿1. 𝐿2 = 64

3. L1 = 8 H
L2 = 8 H
Para XL1 y XL2
𝑿𝑳𝟏 = 𝟐𝝅𝒇𝑳
Suponiendo w =10 rad/seg
𝑋𝐿1 = 10 𝑟𝑎𝑑/𝑠𝑒𝑔(8𝐻)
𝑿𝑳𝟏 = 𝑿𝑳𝟐 = 𝟖𝟎Ω
a) Resistencias y Reactancias
b) Circuito equivalente en el primario
d) VL
12Ω
23 Ω80Ω80Ω
12Ω
I1 8H
120V /_0º
(120 + 𝑗80)𝑰𝟏 − 𝑗40𝑰𝟐 = 120 (Ec 1)
M=4
23Ω
I2
8H
120V /_0º
(12 + 𝑗80)𝑰𝟏 − 𝑗40𝑰𝟐 = 120 (Ec 1)
(23 + 𝑗80)𝑰𝟐 − 𝑗40𝑰𝟏 = 0 (Ec 2)
𝑰𝟏 = 𝟎. 𝟓𝟎 − 𝒋𝟏. 𝟖𝟎 𝑨
𝑰𝟐 = 𝟎. 𝟒𝟕 − 𝒋𝟎. 𝟕𝟔 𝑨
𝑽𝒍 = 𝟏𝟏. 𝟓 − 𝒋𝟒𝟏. 𝟒 𝑽

4. c)
2) Escriba las ecuaciones de malla para la red de la siguiente figura, y
calcule I1, I2 e I3
Solución
12Ω
I1 8H
50V /_0º
(120 + 𝑗80)𝑰𝟏 − 𝑗40𝑰𝟐 = 50
𝑰𝟏 = 𝟎. 𝟑𝟒 − 𝒋𝟏. 𝟔𝟎 𝑨
(𝑍1 + 𝑋𝑙1)𝑰𝟏 − 𝑀12 𝑰𝟐 + 𝑀13 𝑰𝟑 = 𝐸1 (Malla 1)
(𝑍3 + 𝑍2 + 𝑋𝑙2)𝑰𝟐 − 𝑍2𝑰𝟑 − 𝑀12 𝑰𝟏 = 0 (Malla 2)
(𝑍2 + 𝑍4 + 𝑋𝑙3)𝑰𝟑 − 𝑍2𝑰𝟐 + 𝑀13 𝑰𝟏 = 0 (Malla 3)

5. 3) Determine la impedancia de entrada del siguiente transformador y dibuje
la red reflejada.
Solución
De la ecuación de k
𝑴 = 𝟎. 𝟐
 Para la impedancia en el devanado 1
𝒁𝟏 = 𝑹𝟏 + 𝑿𝑳𝟏
𝑍1 = 2 + 𝑗8(1000) = 3 + 𝑗8000
𝒁𝟏 = 𝟑 + 𝒋𝟖𝟎𝟎𝟎
 Para la impedancia en el devanado 2
𝒁𝟐 = 𝟐𝟏 + 𝑿𝑳𝟐 + 𝑹𝑳
𝑍2 = 1 + 𝑗2(1000) + 20 = 21 + 𝑗2000
𝒁𝟐 = 𝟐𝟏 + 𝒋𝟐𝟎𝟎𝟎

6.  Para la impedancia de entrada
𝒁𝒆𝒏𝒕 =
𝑽𝟐
𝑽𝟏
= 𝒁𝟏 −
𝑾 𝟐
𝑴 𝟐
𝒁𝟐
𝑍𝑒𝑛𝑡 = 3 + 𝑗8000 −
10002
0.22
21 + 𝑗2000
𝒁𝒆𝒏𝒕 = 𝟐. 𝟕𝟗 + 𝒋𝟖𝟎𝟏𝟗. 𝟗
M=0.2
L1-M=7.8 L2-M=1.8
V1 V2
+ +
-
-
Red equivalente T