El documento presenta un análisis de un grafo no dirigido y de un dígrafo. En el grafo no dirigido se analizan propiedades como conectividad, regularidad y se presentan cadenas y ciclos. En el dígrafo se encuentran la matriz de conexión, cadenas y ciclos, y se demuestra que es fuertemente conexo aplicando la matriz de accesibilidad.

1. UNIVERSIDAD FERMÍN TORO
VICERRECTORADO ACADEMICO
FACULTAD DE INGENIERÍA
Escuelas Unificadas
LAURA ORTEGA
26.976.713
ESTRUCTURAS DISCRETAS
a) Matriz de adyancencia
V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 0 0 1 1 1
V2 1 0 1 1 1 0 1 0
V3 1 1 0 1 1 0 1 1
V4 1 0 1 0 1 0 0 1
V5 1 0 1 1 0 1 0 1
V6 1 1 0 0 1 0 1 1
V7 0 1 1 0 0 1 0 1
V8 0 1 1 1 1 1 1 0

2. b) Matriz de incidencia
a
1
a
2
a
3
a
4
a
5
a
6
a
7
a
8
a
9
a1
0
a1
1
a
1
2
a13 a1
4
a1
5
a1
6
a17 a1
8
a19 a20
V1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
V2 1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0
V3 0 1 1 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0
V4 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0
V5 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 1 0 0
V6 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1
V7 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1
V8 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 0 1 0
c) ¿Es conexo? Justifique su respuesta
Si es conexo, ya que para cualquier par de vértices existe al menos una trayectoria donde
tienen un camino que los une.
d) ¿Es simple? Justifique su respuesta
Si es simple, debido a que ninguno de los vértices posee lazos ni caminos de regreso.
e) ¿Es regular? Justifique su respuesta
Ya que existen vértices de diferentes grados, no es regular.
f) ¿Es completo? Justifique su respuesta
Ya que de este grafo se pueden obtener otros subgrafos, no es completo.
g) Una cadena simple no elemental de grado 6
C =[V1 a1 V2 a10 V6 a16 V5 a14 V4 a3 V2]
h) Un ciclo no simple de grado 5
Ci=[V5 a19 V8 a18 V7 a17 V5 a19 V7 a9 V2]
i) Arbol generador aplicando el algoritmo constructor
 Elegir S1=V1, y coloca H1= {V1}
 Se elige a a4 que conecta a V1 con V4 y se coloca H2= {V1,V4]
 Se elige la arista a15 que conecta V4 con V7 y se coloca H3={V1,V4}.
 Se elige la arista a 17 que conecta V7 con V5 y se coloca
H4={V1,V4,V7,V5}
 Se elige la arista 19 que conecta V5 con V8 y se coloca H5={V1, V4, V7,
V5,V8}
 Se elige la arista a20 que conecta V8 con V6 y se coloca
H6={V1,V4,V7,V5,V8,V6}

3.  Se elige la arista a10 que conecta V6 con V2 y se coloca H7= {V1, V4, V7,
V5, V8, V6, V2}
 Se elige la arista a3 que conecta V2 con V3 y se coloca H7= {V1, V4, V7,
V5, V8, V6, V2,V3}. Obteniendo de esta manera el siguiente árbol
generador.
j) Subgrafo parcial
k) Demostrar si es euleriano aplicando el algoritmo de Fleury
No es Euleriano, ya que posee vértices de valencia o grado impar.
l) Demostrar si es hamiltoniano
El grafo posee 8 vértices, así que haciendo la división necesaria (8/2) cada vértice debe ser
mayor o igual a 4 para ser hamiltoniano.
V1=5; V2=5; V3=6; V4=4;V5=5; V6=5; V7=4; V8=6.
Debido a esto, el grafo es Hamiltoniano.
a19
a4
V1
a15
V4
V7
a17
V5
V8
a19
V6
a10
V2A3V3
a19
V8
a19
V6V5

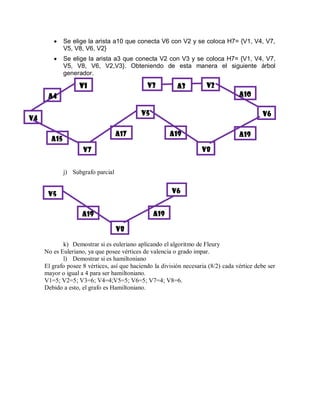
4. Dado el siguiente dígrafo:
a) Encontrar matriz de conexión
A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14
V1 0 0 0 0 0 0 0 0 1 0 0 0 0 0
V2 1 0 0 0 0 0 0 0 0 1 0 0 0 0
V3 0 1 0 0 1 0 0 0 0 0 0 0 0 0
V4 0 0 1 0 0 0 0 1 0 0 1 0 0 0
V5 0 0 0 0 0 1 1 0 0 0 0 0 0 1
V6 0 0 0 1 0 0 0 0 0 0 0 1 0 0
b) ¿Es simple? Justifique su respuesta
No es simple ya que posee aristas paralelas.
c) Encontrar una cadena no simple no elemental de grado 5
C=[ V1 a6 V5 a11 V4 a12 V6 a14 V5 a13 V6]
d) Encontrar un ciclo simple
Ci=[ V5 a11 V4 a12 V6 a14 V5]

5. e) Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad
Así, es fuertemente conexo.
f) Encontrar la distancia de v2 a los demás vértices utilizando el algoritmo de Dijkstra
dv2 a v1: 2
dv2 a V3: 3
dv2 a V5: 3
dv2 a v4: 4
dv2 a v6: 3
0 1 1 0 1 0
0 0 1 1 0 1
0 0 0 1 1 0
1 0 0 0 0 1
0 1 0 1 0 1
0 0 0 0 1 0
0 0 1 1 1 1
1 0 0 1 1 1
1 1 0 1 0 1
0 1 1 0 1 0
1 0 1 1 1 1
0 1 0 1 0 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 0 1 1
0 1 1 1 1 1
0 1 1 1 1 1
1 0 1 1 0 1
1 1 1 1 1 1
1 0 1 1 1 1
0 1 1 1 1 1
1 1 0 1 1 1
1 1 1 1 1 1
1 1 1 1 0 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 0 1
Aristas a
1
a
2
a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14
Ponderación 2 3 4 3 2 3 4 1 4 3 2 2 4 3
Matriz2
Matriz
Matriz3
Matriz4
Matriz5
Matriz
Accesibilidad