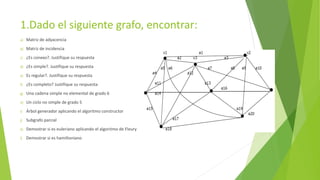
1) El documento presenta una serie de ejercicios sobre grafos, incluyendo encontrar la matriz de adyacencia y de incidencia de un grafo, determinar si es conexo, regular, completo, euleriano o hamiltoniano, y encontrar un árbol generador y subgrafos. 2) También incluye ejercicios para encontrar una cadena y ciclo no simples en un grafo y demostrar si un digrafo es fuertemente conexo usando la matriz de accesibilidad. 3) Por último, pide calcular las distancias desde un vértice a otros usando el

1. Universidad Fermín Toro
Departamento De Formación General
Escuela de Ingeniería
Cabudare
Ejercicios Propuestos
Jesús Camacho
C.I: 28.127.893
Prof. Edecio Freitez
SAIA “A”

2. 1.Dado el siguiente grafo, encontrar:
a) Matriz de adyacencia
b) Matriz de incidencia
c) ¿Es conexo?. Justifique su respuesta
d) ¿Es simple?. Justifique su respuesta
e) Es regular?. Justifique su respuesta
f) ¿Es completo? Justifique su respuesta
g) Una cadena simple no elemental de grado 6
h) Un ciclo no simple de grado 5
i) Árbol generador aplicando el algoritmo constructor
j) Subgrafo parcial
k) Demostrar si es euleriano aplicando el algoritmo de Fleury
l) Demostrar si es hamiltoniano

3. A) Matriz de adyacencia
V1 V2 V3 V4 V5 V6 V7 V8
A1 1 1 0 0 0 0 0 0
A2 1 0 1 0 0 0 0 0
A3 0 1 1 0 0 0 0 0
A4 1 0 0 1 0 0 0 0
A5 1 0 0 0 1 0 0 0
A6 1 0 0 0 0 0 1 0
A7 0 0 1 0 0 0 0 1
A8 0 1 0 0 0 1 0 0
A9 0 1 0 0 0 0 1 0
A10 0 1 0 0 0 0 0 1
A11 0 0 1 1 0 0 0 0
A12 0 0 1 0 1 0 0 0
A13 0 0 1 0 0 1 0 0
A14 0 0 0 1 0 1 0 0
A15 0 0 0 1 1 0 0 0
A16 0 0 0 0 0 1 0 1
A17 0 0 0 0 1 1 0 0
A18 0 0 0 0 1 0 1 0
A19 0 0 0 0 0 1 1 0
A20 0 0 0 0 0 0 1 1
B) Matriz de incidencia
Solución:
V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 1 0 0 1 1
V2 1 0 1 0 1 1 0 1
V3 1 1 0 1 1 1 1 0
V4 1 0 1 0 1 0 1 0
V5 0 1 1 1 0 1 1 1
V6 0 1 1 0 1 0 0 1
V7 1 0 1 1 1 0 0 1
V8 1 1 0 0 1 1 1 0
Ma (G)= Mi (G)=

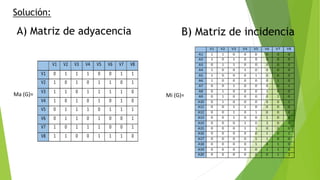
4. C) ¿Es conexo?:
R: Si, por qué existe una conexión entre cada vértice de uno a otro, ya que según la teoría, El grafo G
es conexo, si para cualquier par de vértices a y b en (G) existe al menos una trayectoria de (a) a (b)
donde tienen un camino que los conecte.
D) ¿Es simple?:
R: Si, ya que no posee lazos en ninguno de sus vértices.
E) ¿Es regular?:
R: No, ya que no posee vértices de igual grado o valencia, como: V1= 5, V2= 5, V3= 6, V4= 4, V5= 6,
V6= 4, V7= 5, V8= 5
F) ¿Es completo?:
R: No, por qué no se conectan todos los vértices, sino que sus conexiones son disparejas y no todos los
vértices se conectan, ejemplo (V1 y V6) no posee ninguna arista que los conecte.
G) ¿Posee una cadena simple no elemental de grado 6?:
R: C= [v1 a1 v2 a10 v6 a16 v5 a14 v4 a11 v3 a3 v2] Nos indica que no es elemental, ya que repite el
vértice [v2]
H) Un ciclo no simple de grado 5:
R: C= [v5 a19 v8 a18 v7 a17 v5 a19 v7 a9 v2] Nos indica que no es simple, porque repite la arista [a19]

5. I) Arbol generador aplicando el algoritmo constructor:
5. Elegimos la arista A12 que
conecta a V3 con V7 haciendo
H4=[v1 v4 v3 v7]
V4
A4
V4
A4
3. Elegimos la arista A11 que
conecta a V4 con V3 haciendo
H3=[v1 v4 v3]
1. Se comienza eligiendo
S1=V1 Haciendo H1=[V1]
2. Elegimos la arista A4 que
conecta a V1 con V4 haciendo
H2=[v1,v4]
A11
V4
A4
A11
V7
A12

6. V4
A4
A11
V7
A12
4. Elegimos la arista A17
que conecta a V7 con V5
haciendo H5=[v1 v4 v3 v7
v5]
5. Elegimos la arista A8 que
conecta V5 con V2 haciendo
H6=[V1 v4 v3 v7 v5 v2]
6. Elegimos la arista A9 que
conecta a V2 con V8 haciendo
H7=[v1 v4 v3 v7 v5 v2 v8]
A17
V4
A4
A11
V7
A12 A17
V4
A4
A11
V7
A12 A17
A8
A9
A8

7. 7. Elegimos la arista A20
que conecta a v7 con v8
haciendo H8=[v1 v4 v3 v7
v5 v2 v8 v6]
V4
A4
A11
V7
A12
V5
A17
A8
A9
A20
J) Subgrafo parcial:
1. V4 A4 v1 A2 v3 A3 V2
2. V7 A17 v5 A19 v7 A20 v6
V4
V7
V5

8. I) Demostrar si es euleriano aplicando el algoritmo de Fleury
1. Seleccionamos A1 2. Seleccionamos A3 3. Seleccionamos A2

9. 5. Seleccionamos A11 6. Seleccionamos A124. Seleccionamos A4

10. 7. Seleccionamos A5 9. Seleccionamos A98. Seleccionamos A6

11. 12. Seleccionamos A1311. Seleccionamos A710. Seleccionamos A10

12. 15. Seleccionamos A1813. Seleccionamos A14 14. Seleccionamos A15

13. 16. Seleccionamos A20 17. Seleccionamos A16
Como se puede
observar el grafo
no es Euleriano,
ya que los vértices
no tienen grado
par, lo cual no es
posible construir
un ciclo Euleriano.

14. I) Demostrar si es Hamiltoniano
Es Hamiltoniano
ya que el número
de vértices de G
en 8, Gr (v1) ≥
8/2=4 (i=1,2,8)
A4
A15 A17
A2 A3
A19
A20
A10
V1
V7
V8
V5V4
V3
V2
V6

15. 2.Dado el siguiente diágrafo, encontrar:
a) Matriz de conexión
b) ¿Es simple?. Justifique su respuesta
c) Cadena no simple no elemental de grado 5
d) Ciclo simple
e) Demostrar si es fuertemente conexo
utilizando la matriz de accesibilidad
f) Encontrar la distancia de v2 a los demás
vértices utilizando el algoritmo de Dijkstra

16. A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14
V1 0 0 0 0 0 0 0 0 1 0 0 0 0 0
V2 1 0 0 0 0 0 0 0 0 1 0 0 0 0
V3 0 1 0 0 1 0 0 0 0 0 0 0 0 0
V4 0 0 1 0 0 0 0 1 0 0 1 0 0 0
V5 0 0 0 0 0 1 1 0 0 0 0 0 0 1
V6 0 0 0 1 0 0 0 0 0 0 0 1 1 0
A) Matriz de conexión
B) ¿Es simple?
Si, porque no tiene ningún lazo y tampoco existen arcos
paralelos que puedan partir de un mismo vértice a otro.

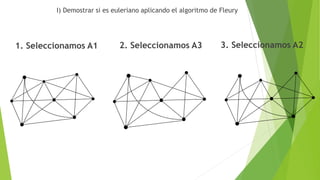
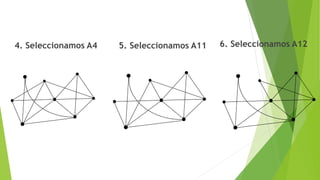
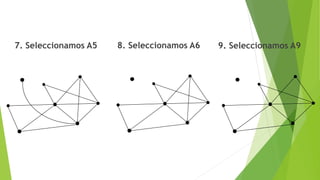
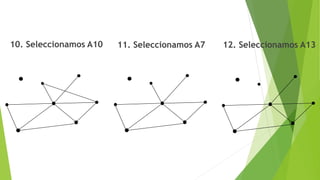
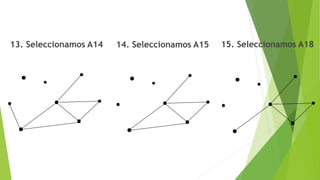
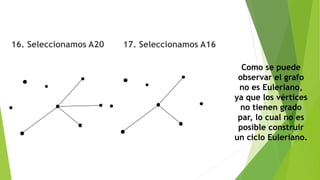
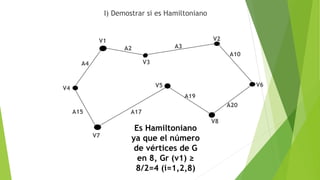
17. C) Encontrar una cadena no simple
no elemental de grado 5:
D) Encontrar un ciclo simple
A6
v1
v5
v4
v6
v5
v4
v6
A11
A13
A12
A14
A11 A12
A14
C= [v1 a6 v5 a11 v4 a12 v6 a14 v5 a13 v6]
C= [v5 a11 v4 a12 v6 a14 v5]

18. E) Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad:
V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0
V1 V2 V3 V4 V5 V6
V1 0 0 1 1 1 1
V2 1 0 0 1 1 1
V3 1 1 0 1 0 1
V4 0 1 1 0 1 0
V5 1 0 1 1 1 1
V6 0 1 0 1 0 1
V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 0 1 1 1 1
V3 0 1 1 1 1 1
V4 1 1 0 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 0 1
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 1 1 1 1 1
V3 1 1 1 1 1 1
V4 1 1 1 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 0 1
MA (D)=
M2 (D)=
M3 (D)=
M4 (D)=
M5 (D)=

19. V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 1 1 1 1 1
V3 1 1 1 1 1 1
V4 1 1 1 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 1 1
V1 V2 V3 V4 V5 V6
V1 3 4 5 4 5 4
V2 4 2 5 5 5 5
V3 3 4 3 4 4 4
V4 4 4 3 5 4 4
V5 3 4 4 5 4 5
V6 3 3 3 4 1 4
Acc(D)= Bin
• Componentes iguales a cero (0)
permanecerá como cero (0)
• Componentes diferentes de cero
(0) se convertirá en uno (1)
Dígrafo fuertemente conexo
Acc(D)= Bin

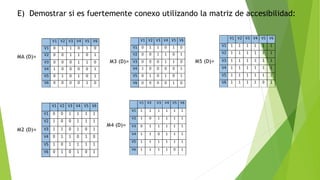
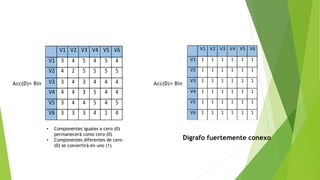
20. F) Encontrar la distancia de v2 a los demás vértices utilizando el algoritmo de Dijkstra:
Aristas A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 A11 A12 A13 A14
Ponderación 2 3 4 3 2 3 4 1 4 3 2 2 4 3
Ponderación de las aristas:
A1v1
v5
v4
v6
A11
A13
A12
A14
A10
A7
v3
v2
A9
A2
A4
A6
A3
A5
A8
[2,2] (1)
[0] (0)
[3,2] (1)
[3,2] (1)
[3,2] (1)
Dv2 a v1: 2
Dv2 a v3: 3
Dv2 a v5: 3
Dv2 a v4: 4
Dv2 a v6: 3
[4,2] (1)