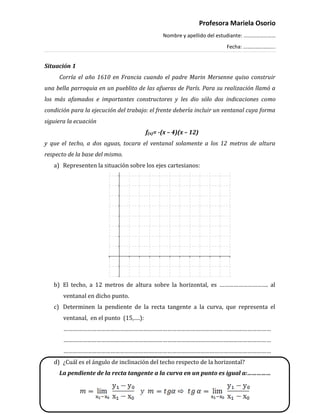
El documento describe dos situaciones relacionadas con conceptos de derivadas. La primera situación describe la construcción de una parroquia en Francia en 1610, donde se especifican condiciones sobre la forma de un ventanal y la inclinación del techo. La segunda situación presenta gráficos de funciones para analizar la existencia de derivadas y tangentes en puntos. Se piden cálculos de pendientes de rectas tangentes y secantes, y se analizan propiedades de funciones derivables.