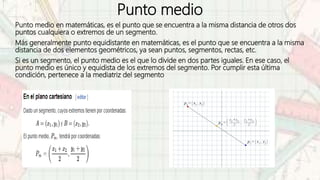
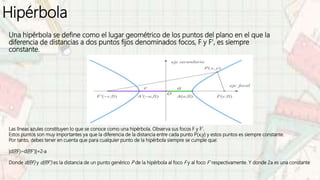
El documento explica el concepto del plano cartesiano, su uso para localizar puntos en el plano y analizar figuras geométricas como parábolas, elipses y hipérbolas. Se describen características clave de estas figuras y métodos para calcular distancias y puntos de intersección con los ejes coordenados. También se ofrecen definiciones importantes para comprender la geometría analítica y las propiedades de las distintas formas geométricas.