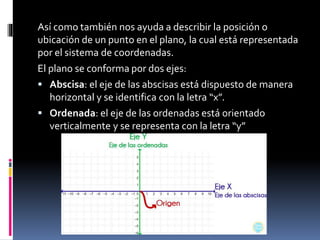
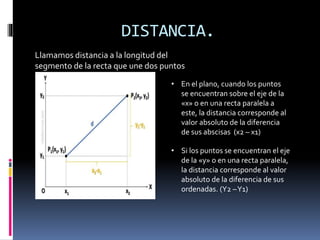
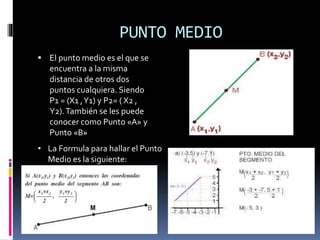
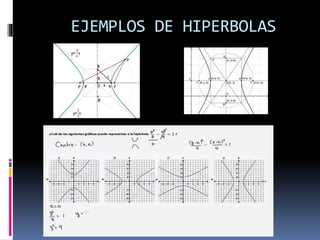
El documento describe los conceptos básicos del plano cartesiano o numérico, incluyendo sus ejes, cuadrantes, y cómo se usa para describir la posición de puntos. También explica conceptos como distancia, punto medio, ecuaciones y cómo trazar figuras geométricas como circunferencias, parábolas, elipses e hipérboles en el plano cartesiano.

1. PLANONUMERICO
LUCIA ESPINOLA
C.I. 19.106.797
SECCION: CO 0405
REPÚBLICA BOLIVARIANA DEVENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA EDUCACION
UNIVERSITARIA
UNIVERSIDAD POLITECNITATERRITORIAL ANDRES ELOY
BLANCO
BARQUISIMETO, EDO LARA

2. PLANO NUMÉRICO
 El plano numérico o plano cartesiano,
también conocido como sistema cartesiano
de coordenadas; son dos rectas numéricas
perpendiculares, una vertical y la otra
horizontal que se cortan en un punto origen
llamada cero. Este nos ayuda a analizar
matemáticamente figuras geométricas como
la parábola, la hipérbole, la línea, la
circunferencia y la elipse, las cuales forman
parte de la geometría analítica

3. Así como también nos ayuda a describir la posición o
ubicación de un punto en el plano, la cual está representada
por el sistema de coordenadas.
El plano se conforma por dos ejes:
 Abscisa: el eje de las abscisas está dispuesto de manera
horizontal y se identifica con la letra “x”.
 Ordenada: el eje de las ordenadas está orientado
verticalmente y se representa con la letra “y”

4. También cuenta con cuatro cuadrantes:
Se llama cuadrantes a las cuatro áreas que se forman por la unión de las
dos rectas perpendiculares. Los puntos del plano se describen dentro de
estos cuadrantes.
 Cuadrante I: la abscisa y la ordenada son positivas.
 Cuadrante II: la abscisa es negativa y la ordenada positiva.
 Cuadrante III: tanto la abscisa como la ordenada son negativas.
 Cuadrante IV: la abscisa es positiva y el ordenada negativa.

5. DISTANCIA.
Llamamos distancia a la longitud del
segmento de la recta que une dos puntos
• En el plano, cuando los puntos
se encuentran sobre el eje de la
«x» o en una recta paralela a
este, la distancia corresponde al
valor absoluto de la diferencia
de sus abscisas (x2 – x1)
• Si los puntos se encuentran el eje
de la «y» o en una recta paralela,
la distancia corresponde al valor
absoluto de la diferencia de sus
ordenadas. (Y2 –Y1)

6.  Pero si los puntos se encuentran en cualquier lugar del sistema
de coordenadas; la distancia quedará determinada por la
relación.
 Ej: Hallar la distancia en el plano entre dos puntos cuyas
coordenadas son: P1 = (-3 , 5) y P2 = (-7, 1)

7. PUNTO MEDIO
 El punto medio es el que se
encuentra a la misma
distancia de otros dos
puntos cualquiera. Siendo
P1 = (X1 ,Y1) y P2= ( X2 ,
Y2).También se les puede
conocer como Punto «A» y
Punto «B»
• La Formula para hallar el Punto
Medio es la siguiente:

8. ECUACIONES.
 Una Ecuación es una igualdad de dos expresiones donde existe una o
varias variables o incógnitas.
Ej. X + 5 = 4 ó 2X = 10.
 Las ecuaciones se pueden clasificar en:
 Ecuaciones algebraicas:
A. Lineales o de primer grado: Es la que involucra solo variables a la
primera potencia. Ej. 3x + 2y = 5
B. Cuadráticas o de tercer grado: Es aquella donde al menos una de las
variables se encuentra elevada a la 2da potencia Ej: 3x2 + 3x= x-1
C. Cúbica o de tercer grado: Esta ecuación la podemos poner bajo la
forma canónica ( ax³ + bx² + cx + d= 0 ) Ej. 2x³+3x² - 3x+2=10

9. E. Diofántica: Son todas aquellas que pertenecen a los números
enteros y tienen la forma de (ax+by=c) Ej. 2x+5y=59
F. Racionales: Son aquellas cuyo primer termino contiene un cociente
de polinomios (P (x) / Q(y) = 0) Ej. X² + 4X + 3 = 0
X
 EcuacionesTrascendentes: Son aquellas cuyo valor no se obtiene al
realizar algún conjunto de operaciones con variables.
 Ecuaciones diferenciales: Son las que relacionan una función con sus
derivadas
 Ecuaciones Funcionales: En esta ecuación algunas de las constantes
y variables que intervienen no son realmente números sino
funciones.

10. TRAZADO DE CIRCUNSFERENCIA
Una circunferencia es el lugar geométrico
donde los puntos de un plano equidistan de
otro punto fijo llamado centro.
Los elemento de la circunferencia son:
a) CENTRO: Es el punto interior cuya
distancia entre el cualquier otro punto es
la misma.
b) RADIO: Es el segmento que une el centro
con cualquier otro punto.
c) DIAMETRO: Es el segmento que une 2
puntos de la circunferencia y que pasa por
el centro (es el doble del radio: D=2R).
d) CUERDA: Es el segmento que 2 puntos de
la circunferencia.
e) ARCO: Parte de la circunferencia
comprendida por dos puntos.
f) SEMICIRCUNFERENCIA: Es cualquiera de
las dos partes en que el diámetro divide a
la circunferencia.

11.  NOTA: Para poder trazar una circunferencia en el plano es
necesario conocer el centro y el radio, de no ser así debemos
hallarlo.
Si Conocemos los datos de el Diámetro (en el enunciado se nos
dan dos puntos de coordenadas ) podemos encontrar el centro
con la ecuación del Punto Medio
Una vez que tenemos el Centro, calculamos el radio tomando
como datos uno de los dos puntos dados en el enunciado (el
diámetro) y el centro, podemos calcularlo con la formula de la
distancia
A partir de aquí podemos usar la ecuación canónica
(X – H)² + (Y – K)² = r²

12. Ejemplo:

13. PARÁBOLA
 Es el lugar geométrico de los puntos de un plano equidistante de
un punto fijo llamado foco y de una recta fija llamada directriz.

14. LA ELIPSE
 Es el lugar geométrico de un punto que se mueve en un plano de
manera que la suma de sus distancias a dos puntos fijos de ese plano
es siempre igual a una constante, mayor que la distancia entre los
dos puntos

15. LA HIPERBOLA
 Es el lugar geométrico de los
puntos del plano cuya
diferencia de distancia a los
puntos fijos (focos) es
constante en valor absoluto
con el eje focal.
Los puntos B y B' se obtienen como
intersección del eje imaginario con la
circunferencia que tiene por centro uno
de los vértices y de radio c.
6. Radios vectores: Son los segmentos
que van desde un punto de la hipérbola
a los focos: PF y PF'.
7. Distancia focal: Es el segmento de
longitud 2c.
8. Eje mayor: Es el segmento de
longitud 2a.
9. Eje menor: Es el segmento de
longitud 2b.
10. Ejes de simetría: Son las rectas que
contienen al eje real o al eje imaginario.
11. Asíntotas: Son las rectas de
ecuaciones:
12. Relación entre los semiejes:
Elementos de la hipérbola:
1. Focos: Son los puntos fijos F y
F'.
2. Eje principal o real: Es la recta
que pasa por los focos.
3. Eje secundario o imaginario:
Es la mediatriz del segmento
FF'.
4. Centro: Es el punto de
intersección de los ejes.
5.Vértices: Los puntos A y A' son
los puntos de intersección de la
hipérbola

16. EJEMPLOS DE HIPERBOLAS

17. REPRESENTACIONES GRÁFICAS