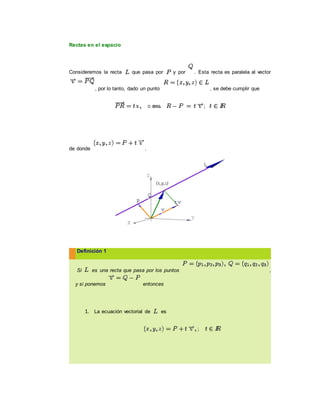
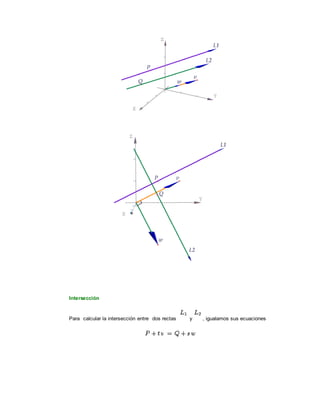
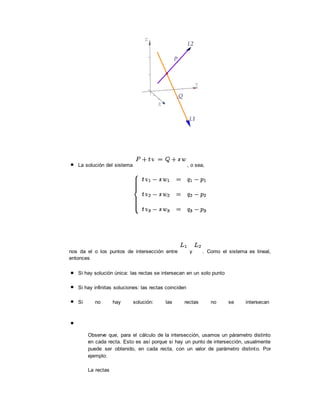
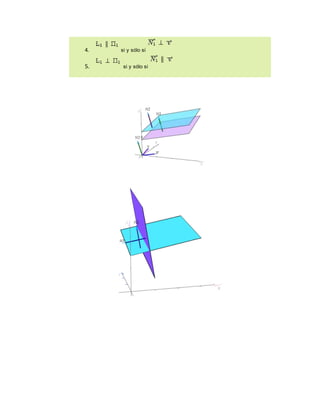
El documento describe las ecuaciones que definen rectas y planos en el espacio tridimensional. Explica cómo obtener las ecuaciones vectoriales, paramétricas y simétricas de una recta, así como las ecuaciones normales, vectoriales y cartesiana de un plano. También cubre conceptos como paralelismo, perpendicularidad e intersección entre rectas y planos.

1. Rectas en el espacio
Consideremos la recta que pasa por y por . Esta recta es paralela al vector
, por lo tanto, dado un punto , se debe cumplir que
de donde .
Definición 1
Si es una recta que pasa por los puntos ,
y si ponemos entonces
1. La ecuación vectorial de es

2. 2. Despejando obtenemos las ecuaciones parámetricas de
3. Si cada , despejando obtenemos las ecuaciones simétricas
de
Como podemos escoger dos puntos cualesquiera (distintos) de una recta para
obtener una ecuación, las ecuación de una recta no es única.
EJEMPLO 1
Consideremos la recta que pasa por y . En
este caso , luego

3. 1. Ecuación vectorial:
2. Ecuaciones parámetricas:
3. Ecuaciones simétricas:
Observe que el segmento que va de a es el conjunto de puntos

4. En particular, si , obtenemos el punto medio del segmento
Ángulo,paralelismo, perpendicularidad e intersección
Definición 2
Consideremos dos rectas,
1. si y sólo si
2. si y sólo si
3. El ángulo entre y es igual al ángulo entre y

5. Intersección
Para calcular la intersección entre dos rectas y , igualamos sus ecuaciones

6. La solución del sistema , o sea,
nos da el o los puntos de intersección entre y . Como el sistema es lineal,
entonces
Si hay solución única: las rectas se intersecan en un solo punto
Si hay infinitas soluciones: las rectas coinciden
Si no hay solución: las rectas no se intersecan
Observe que, para el cálculo de la intersección, usamos un párametro distinto
en cada recta. Esto es así porque si hay un punto de intersección, usualmente
puede ser obtenido, en cada recta, con un valor de parámetro distinto. Por
ejemplo:
La rectas

7. ,
se intersecan en el punto .
Este punto se obtiene con en la primera recta y con en la
segunda recta.
EJEMPLO 2
Consideremos la recta de ecuaciones simétricas
va en la dirección de
1. es paralela a la recta pues
2. es perpendicular a la recta
pues
3. no interseca a pues el sistema

8. no tiene solución (hay una clara inconsistencia entre la segunda y tercera
ecuación).
Planos en el espacio tridimensional.
Ecuación vectorial, normal y cartesiana
Así como una recta esta determinada por dos puntos distintos, un plano está
determinado por tres puntos no colineales.
Una manera muy conveniente de obtener una ecuación del plano en que
pasa por los puntos , es observar que los puntos tienen la
propiedad
Esta ecuación es una ecuación normal de

9. Si ponemos y desarrollamos la ecuación anterior,
obtenemos una ecuación cartesiana de
Finalmente, podemos observar que si está en , entonces
Esta es una ecuación vectorial de .

10. Definición 3
Consideremos un plano que pasa por los puntos no colineales .
1. es un vector normal al plano
si para cualquier .
2. Si es un vector normal al plano entonces
se llama una ecuación normal de
3. Si es un vector normal del plano entonces

11. se llama una ecuación cartesiana del plano
4. Si y si entonces
se llama una ecuación vectorial del plano
Tres puntos y
son no colineales si
EJEMPLO 3
Consideremos un plano que pasa por los puntos no colineales
y
1. Ecuación vectorial:
2. Ecuación cartesiana: un vector normal es
. Como
, una ecuación cartesiana es

12. Paralelismo, perpendicularidad y ángulo
Definición 4
Consideremos una recta y dos planos de ecuación
cartesiana
Entonces, siendo y , normales a
y , respectivamente,
1. si y sólo si
2. si y sólo si
3. El ángulo entre los planos es el ángulo entre los vectores normales

13. 4. si y sólo si
5. si y sólo si

14. EJEMPLO 4
Consideremos tres puntos no
colineales. Para obtener un punto tal que los cuatro puntos conformen un
paralelogramo, debemos escoger de la siguiente manera
Esto es así puesto que debe estar en el plano que contiene a .

15. EJEMPLO 5
Consideremos el problema de obtener la ecuación cartesiana del plano que
contenga a la recta
y al punto (que no está en ).
Para encontrar la ecuación cartesiana del plano , buscamos tres puntos no
colineales en este plano; podemos considerar el punto que ya tenemos y dos
puntos de la recta.
Para obtener estos dos puntos de la recta, le damos una par de valores al
parámetro , en la recta, tal que nos generen dos puntos adicionales. Digamos que
ponemos y . Así, tres puntos en el plano son

16. Observe que ,así que son puntos no colineales
Bien, ahora tomemos .
Como , una ecuación cartesiana es
EJEMPLO 6
Consideremos el problema de obtener la ecuación cartesiana del plano que sea
paralelo, simúltaneamente, a las rectas
y que contenga al punto

17. De acuerdo a la teoría, un vector normal a debe ser perpendicular a y
a ; entonces para encontrar la ecuación cartesiana del plano , podemos
tomar . Como , una
ecuación cartesiana es
EJEMPLO 7
Consideremos el problema de obtener la ecuación cartesiana del plano que sea
perpendicular a la recta
y que contenga al punto
Para encontrar la ecuación cartesiana del plano , podemos
tomar . Como , una ecuación cartesiana es