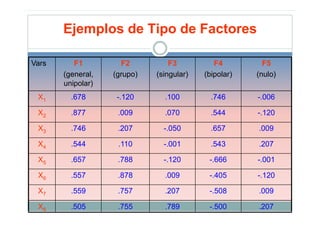
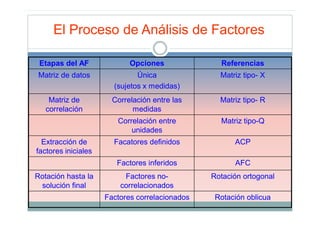
Este documento describe el análisis de factores como una técnica estadística multivariada que reduce un conjunto de variables a un número menor de factores subyacentes. Explica que el análisis de factores busca identificar las variables latentes comunes que explican las correlaciones entre las variables observadas originales. También detalla los diferentes métodos de factorización y tipos de factores, así como las aplicaciones e implicaciones del análisis de factores para el desarrollo de instrumentos.

1. Universidad Pedagógica Experimental Libertador
Programa de Doctorado en Educación
ANÁLISIS DE FACTORES
Carlos Ruiz Bolívar, PhD
cruizb14@gmail

2. Analisis de Factores: Caracteristicas
Tiene capacidad para reducir una matriz de datos a
dimensiones estructurales más pequeñas.
Permite apreciar hasta dónde existe algún patrón
subyacente de relaciones en los datos de la matriz.
Reduce las medidas a un conjunto más pequeño de
factores.
Los factores pueden ser tomados como variables
originarias que explican las interrelaciones
observadas en los datos.

3. Variables Subyacentes
El Análisis Factores parte del supuesto de que en un
conjunto de variables intercorrelacionadas, dichas
relaciones recíprocas podrían deberse a la
presencia de una o más variables (factores
subyacentes) relacionadas en grados diversos con
aquéllas.
El propósito del AF es identificar esos factores o
variables comunes, más generales que los datos
mismos.

4. Análisis de Factores y Varianza
El Análisis de Factores permite descomponer la varianza
implícita en la matriz de datos en dos grandes componentes:
V. Común + V. Única = V. Total
La varianza única, a su vez, se descompone en:
V. Especifica + V de Error = V. Única
V. Común: Se forma por las combinaciones lineales de
variables que están correlacionadas para formar la
comunalidad (h2) Así, la V. Única = 1 – h2
El Análisis de Factores está interesado en extraer toda la
varianza común e ignorar la Varianza única.

5. ¿Qué es un Factor?
Desde el punto de vista matemático, un factor puede
ser definido como cualquier combinación lineal de
variables en la matriz de datos. Ejemplo: Sea el factor
A formado por las variables a, b, c...k y sus
ponderaciones fueran pa, pb, pc...pk su expresión
algebraica sería:
A = paa + pbb + pcc...pkk

6. Interpretaciones sobre los Factores
Como indicadores de efectos
Las variables observadas son consideradas como
el resultado de una variable subyacente latente.
Como componente
Las variables son transformadas en otras
variables por conveniencia.
Como indicadores causales
Las variables latente es considerada como el
resultado de las observables.

7. Origen del Análisis de Factores
• El Análisis de Factores fue creado por Spearman
(1904),
• Su propósito era el de probar su teoría de la
inteligencia,
• El sostenía que en todas las habilidades mentales
subyacía un factor general (común) que denominó
g y factores específicos independientes.

8. Métodos de Factorización
Método Clásico
Se basa en la creencia de que las correlaciones
observadas en la matriz son principalmente el
resultado de alguna regularidad subyacente a los
datos.
Componentes Principales
Es un método de transformación directa de un
conjunto dado de variables dentro de un nuevo
conjunto de variables compuestas o componentes
principales.

9. Tipos de Factores
General: Variables cargan en un mismo factor
De Grupo: Sólo algunas Variables son salientes
Común: Variables que miden el mismo factor
Unipolar: Variables con un mismo signo
Bipolar: Variables con signos + y -
Singular: una sola saliente
Nulo: No tiene saliente

10. Ejemplos de Tipo de Factores
Vars F1 F2 F3 F4 F5
(general, (grupo) (singular) (bipolar) (nulo)
unipolar)
X1 .678 -.120 .100 .746 -.006
X2 .877 .009 .070 .544 -.120
X3 .746 .207 -.050 .657 .009
X4 .544 .110 -.001 .543 .207
X5 .657 .788 -.120 -.666 -.001
X6 .557 .878 .009 -.405 -.120
X7 .559 .757 .207 -.508 .009
X8 .505 .755 .789 -.500 .207

11. Aplicaciones del Análisis de Factores
Como técnica exploratoria
Examinar estructura subyacente a una base de datos
Como técnica confirmatoria
Probar la hipótesis acerca de la estructura subyacente
en la base de datos
Como técnica de medición
En la construcción índices a partir de los coeficientes
de las cargas factoriales

12. El Proceso de Análisis de Factores
Etapas del AF Opciones Referencias
Matriz de datos Única Matriz tipo- X
(sujetos x medidas)
Matriz de Correlación entre las Matriz tipo- R
correlación medidas
Correlación entre Matriz tipo-Q
unidades
Extracción de Facatores definidos ACP
factores iniciales
Factores inferidos AFC
Rotación hasta la Factores no- Rotación ortogonal
solución final correlacionados
Factores correlacionados Rotación oblicua

13. Desarrollo de Instrumentos
La información obtenida a partir del Análisis de
Factores permite:
• Realizar el análisis de item del instrumento
• Estimar la validez de constructo
• Estimar la confiabilidad del instrumento