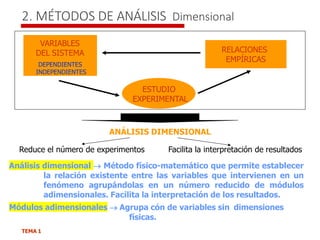
El documento describe los métodos de análisis dimensional para establecer relaciones entre variables que influyen en un fenómeno físico. El análisis dimensional reduce el número de experimentos necesarios y facilita la interpretación de resultados agrupando variables en módulos adimensionales. Se explican conceptos como ecuaciones dimensionales, propiedades de las ecuaciones dimensionales, y aplicaciones del análisis dimensional para determinar dimensiones físicas como velocidad, cantidad de movimiento, aceleración, trabajo y potencia.

1. 2. MÉTODOS DE ANÁLISIS Dimensional
I
ESTUDIO
EXPERIMENTAL
RELACIONES
EMPÍRICAS
VARIABLES
DEL SISTEMA
DEPENDIENTES
INDEPENDIENTES
ANÁLISIS DIMENSIONAL
Reduce el número de experimentos Facilita la interpretación de resultados
Análisis dimensional  Método físico-matemático que permite establecer
la relación existente entre las variables que intervienen en un
fenómeno agrupándolas en un número reducido de módulos
adimensionales. Facilita la interpretación de los resultados.
Módulos adimensionales  Agrupa cón de variables sin dimensiones
físicas.
TEMA 1

2. PRINCIPIOS EN LOS QUE SE FUNDAMENTA EL ANÁLISIS DIMENSIONAL
Resultados
análisis dimensional
Todas las variables que influyen en el fenómeno físico
Comprobación experimental de las relaciones empíricas
TEMA 1
Ecuación Dimensional
El símbolo utilizado para representar una ecuación dimensional son los
corchetes [ ].
Dentro del corchete se coloca la letra que simboliza la magnitud física.
Ejemplo:
[A]: Se lee la ecuación dimensional de A[A]: Se lee la ecuación dimensional de
A ó simplemente la dimensión de A
Las ecuaciones dimensionales de magnitudes físicas se representan por letras o
símbolos.

3. Ejemplos:
[Longitud] = L; se lee «la ecuación dimensional de la
longitud es L» [Longitud] = L; se lee «la ecuación dimensional
de la longitud es L»
[Masa] = M ; se lee «la ecuación dimensional de la masa es
M»[Masa] = M ; se lee «la ecuación dimensional de la masa es
M»
[Tiempo] = T ; se lee «la ecuación dimensional del tiempo es
T»[Tiempo] = T ; se lee «la ecuación dimensional del tiempo es
T»
[Temperatura] = θ ; se lee la ecuación dimensional de la
temperatura es θ [Temperatura] = θ ; se lee la ecuación
dimensional de la temperatura es θ

4. Tabla 1 Fórmulas Dimensionales de
las Magnitudes Fundamentales

5. Propiedades de las Ecuaciones Dimensionales
1. Ecuación dimensional de un producto.
La ecuación dimensional de un producto es el producto de ecuaciones
dimensionales.
[AB]=[A][B]
2. Ecuación dimensional de un cociente.
La ecuación dimensional de un cociente es el cociente de ecuaciones
dimensionales.
[AB]=[A][B][AB]=[A][B]
3. Ecuación dimensional de una potencia o raíz
La ecuación dimensional de una potencia es la ecuación dimensional
de la base elevada a su exponente.
[An]=[A]n[An]=[A]n
La ecuación dimensional de una raíz es la raíz de la ecuación
dimensional del radicando.
[n√A]=n√[A][An]=[A]n

6. Propiedades de las Ecuaciones Dimensionales
4. Ecuación dimensional de un número o cantidad adimensional
La ecuación dimensional de un número (cantidad sin
dimensión) es 1.
[Cantidad adimensional]=1
Ejemplos:
[45o]=1[45o]=1 [ángulo]=1
[tg30o]=1 [tg30o]=1 [función trigonométrica]=1
[log4]=1 [log4]=1 [logaritmo] =1
[√π]=1[π]=1 [número]=1

7. 2 Velocidad
La velocidad se define como la derivada de la posición respecto al tiempo. Una derivada no
es más que un cociente entre dos cantidades muy pequeñas y por tanto sus dimensiones
serán las del numerador divididas por las del denominador, esto es,
La unidad en el SI de velocidad es 1 m/s.

8. 3 Cantidad de movimiento
La cantidad de movimiento es el producto de la masa por la velocidad, por lo que sus
dimensiones serán las del producto de estas dos cantidades:
La unidad SI de la cantidad de movimiento es 1 kg·m/s.
4 Aceleración
La aceleración es la derivada de la velocidad respecto al tiempo, por tanto
La unidad de aceleración en el SI será 1 m/s².

9. 6 Trabajo
El trabajo se define a partir de una integral, esto es, una suma de muchas cantidades muy pequeñas.
Las dimensiones de la integral son entonces las mismas que las de cada uno de los sumandos. Cada
sumando es un trabajo diferencial, igual al producto escalar de una fuerza por un desplazamiento. Por
ello
Vemos que el trabajo posee dimensiones de masa por velocidad al cuadrado, que son las mismas de
la energía cinética
La unidad de trabajo en el sistema internacional es el julio, equivalente a

10. 7 Potencia
La potencia es el cociente entre un trabajo diferencial y el tiempo diferencial en que se realiza. Las
dimensiones las da también el cociente
La unidad SI de potencia es el vatio, que equivale a

11. Si A es una magnitud física,,entonces [A] es la dimensión de la magnitud
física A.
Si x:tiempo entonces :[x]=T
Si v:velocidad entonces :[v]=LT⁻1

12. S O L U C I Ó N :
V E A M O S E L P R I N C I P I O D E H O M O G E N E I D A D Y O B S E R VA R C O M O Q U E D A R Á N U E S T R A
F Ó R M U L A :
[ K V ] = [ F T ]
S E PA R A N D O :
[ K ] [ V ] = [ F ] [ T ]
R E V I S A M O S N U E VA M E N T E N U E S T R A TA B L A D E M A G N I T U D E S F Í S I C A S :
[ K ] LT − 1 = M LT − 2 T
D E S P E J A N D O :
[ K ] = M LT − 2 T LT − 1 = M T − 2 + 1 T − 1 = M T − 1 T − 1 = M
O B S E R VA M O S Q U E K R E P R E S E N TA A L A M AS A.
Problema 1. La siguiente es una fórmula física correcta: Kv = Ft, donde v: velocidad, F: fuerza, t: tiempo. qué magnitud
representa K?

13. Problema 2. La siguiente expresión es dimensionalmente correcta y homogénea: KF = mv²,
donde F: fuerza, m: masa, v: velocidad. qué magnitud representa K?
Solución:
Por principio de homogeneidad dimensional, tenemos:
[KF]=[mv2]
Separamos:
[K][F]=[m][v2]
Buscamos nuestra tabla de magnitudes físicas:
[K]MLT−2=ML2T−2
A simple vista observamos que nuestro resultado será:
[K]=ML2T−2MLT−2=L
Y esto nos conduce a decir que K representa a la longitud

14. EJERCICIOS DE TAREA