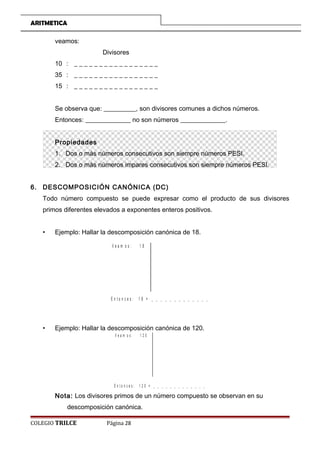
Este documento presenta conceptos básicos sobre el sistema de numeración decimal. Explica que un sistema de numeración utiliza símbolos y reglas para representar números. Luego describe las características del sistema decimal, incluyendo la descomposición polinómica de un numeral, los valores absolutos y relativos de las cifras, y diferentes sistemas de numeración como el binario, ternario y otros. Finalmente, introduce conceptos como la base de un sistema y los principios fundamentales para representar números en diferentes bases.

1. ARITMETICA
III BIM.
TRILCE PRIMARIA

2. ARITMETICA
Í n d i c e
Pág.
¯ Sistema de númeración decimal: descomposición.......7
¯ Sistema de numeración no decimal...........................13
¯ Cambio de Sistema de numeración...........................19
¯ Repaso de Sistema de numeración...........................25
¯ Propiedades de los números......................................29
¯ Criterios de divisivilidad..............................................37
¯ Máximo Común Divisor - Mínimo Común Múltiplo......43
¯ CÌtaqdr`v bts rbr ƒ rbc %
COLEGIO TRILCE Página 2

3. ARITMETICA
CONCEPTOS BÁSICOS
N u m e r a l : E s la f ig u r a o
s ím b o lo q u e r e p r e s e n t a o d a
la id e a d e l n ú m e r o .
N ú m e r o : E s u n a id e a d e c a n t i d a d , la
c u a l n o s p e r m it e c u a n t if ic a r lo s o b j e t o s ;
e s u n e n t e a b s t r a c t o .
* Sistema de numeración
Es un conjunto de símbolos y leyes que nos permiten representar y expresar
correctamente los números.
Tenemos diversos Sistemas de Numeración, entre los cuales destaca el Sistema de
Numeración de Decimal o decuplo
SISTEMA DE NUMERACIÓN DECIMAL
Es el sistema cuyo principio fundamental es que la agrupación de sus unidades son de diez en diez. Así por
ejemplo:
COLEGIO TRILCE Página 3
1 1 u n id a d
1 0 u n id a d e s 1 d e c e n a
1 0 d e c e n a s 1 c e n t e n a
...

4. ARITMETICA
Características del sistema Decimal
a. Símbolos utilizados en el sistema decimal.
  
cifras
9;8;7;6;5;4;3;2;1;0
b. De la combinación de estas cifras se pueden formar todos los números que
conocemos:
Ejemplo:
- Con 0; 1; 2 se pueden formar: 0; 1; 2; 10; 20; 11; 12; 210; . . .
- Con 3; 4; 0 se pueden formar: ___; ___; ___; ___; ___; ___; ___; ___; . . .
Descomposición polinómica de un Numeral del Sistema Decimal
Cualquier número se puede descomponer como la suma de los valores relativos de sus
cifras.
Ejemplo: 3 2 7 8 = 3000 + 200 + 70 + 8
= ___ × 10
3
+ ___ + 10
2
+ ___ × 10
1
+ 8
Observa: Cada cifra está multiplicada por 10 y ésta tiene como exponente la
cantidad de cifras que se encuentran as la derecha de ella.
3 2 7 8
3 × 1 0 3
3 2 7 8
2 × 1 0 2
3 2 7 8
7 × 1 0 1
3 2 7 8
8 × 1 0 0
Forma general
. . . b c b a = . . . + d × 1 0 + c × 1 0 + b × 1 0 + a13 2
Casos especiales
* mmmm = m × 10
3
+ m × 10
2
+ m × 10
1
+ m
= 1000m + 100m + 10m + m = 1111m
COLEGIO TRILCE Página 4

5. ARITMETICA
* Para un numeral capicúa:
aba = a × 10
2
+ b × 10
1
+ a
= 100a + 10b + a = 101a + 10b
abcba = a × 10
4
+ b × 10
3
+ c × 10
2
+ b × 10
1
+ a
= 10000a + 1000b + 100c + 10b + a = 10
= _______ × a + _______ × b + _______ × c
c. En el sistema decimal:
- Mínimo valor no significativo : 0
- Mínimo valor significativo : 1
- Máximo valor : 9
Orden: Es la posición que ocupa cada cifra empezando a contar de derecha a
izquierda.
Ejemplo:
U
4
1 e r
D
3
2 d o
C
2
3 e r
U M
1
4 t o
1 o r d e n o u n i d a d e s . . . . = _ _ _ _ _ _ _ _
2 o r d e n o d e c e n a s
e r
d o
e r
t o
. . . . = _ _ _ _ _ _ _ _
3 o r d e n o c e n t e n a s . . . . = _ _ _ _ _ _ _ _
4 o r d e n o u n id a d e s d e m il la r . . . . = _ _ _ _ _ _ _ _
Lugar: Es la ubicación de la cifra según como se lee, de izquierda a derecha.
Ejemplo:
U
4
1 e r
D
3
2 d o
C
2
3 e r
U M
1
4 t o
1 L u g a r = _ _ _ _ _ _ _ _
2
e r
d o
e r
t o
L u g a r = _ _ _ _ _ _ _ _
3 L u g a r = _ _ _ _ _ _ _ _
4 L u g a r = _ _ _ _ _ _ _ _
Valores de una cifra
Toda cifra que forma parte de un número, puede tener dos valores.
a. Valor absoluto (V.A.): Es absolutamente el mismo valor de cada cifra en cualquier
orden que se encuentre.
COLEGIO TRILCE Página 5

6. ARITMETICA
7 5 1 4
V . R . ( 4 ) = _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
V . R . ( 1 ) = _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
V . R . ( 5 ) = _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
V . R . ( 7 ) = _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
V . A . ( 7 ) = _ _ _ _ _ _ _ _
V . A . ( 5 ) = _ _ _ _ _ _ _ _
V . A . ( 1 ) = _ _ _ _ _ _ _ _
V . A . ( 4 ) = _ _ _ _ _ _ _ _
b. Valor Relativo (V.R.): Es relativo al orden donde se encuentra cada cifra (unidades,
decenas, centenas, . . .)
¡ LISTOS A TRABAJAR ¡
1. Escribe el valor relativo (V.R.) o el valor absoluto (V.A.) según corresponda.
a. 34 271 → V.R.(2) = _____________
b. 67 192 → V.A.(6) = _____________
c. 5 314 218 → V.R.(4) = _____________
d. 27 235 → V.A.(7) = _____________
e. 851 231 → V.R.(8) = _____________
f. 567 421 → V.A.(5) = _____________
2. Indicar la suma de la cifra del primer orden más la cifra del sexto orden en:
42 399 981 301
3. Indicar la suma de la cifra del tercer lugar más la cifra del quinto lugar en:
29 433 167
4. Calcular la suma del mayor y menor número que se puede formar con las siguientes
cifras, solo puedes utilizar una vez cada cifra.
1; 2; 4; 7; 9
5. ¿Cuál debe ser el valor de x en: 2323xxx2x332x =++ ?
COLEGIO TRILCE Página 6

7. ARITMETICA
6. Si se cumple que: a22 es el triple de a7 . Calcular el valor de a.
7. Hallar el valor de a y b tal que: b123 es el doble de a1a .
8. Hallar el valor de b, si se cumple que: b78 es el resultado de invertir el orden de las
cifras a 87b y disminuirlo en 99 unidades.
9. Hallar un número de dos cifras, ambas diferentes de cero, tal que al restarle el mismo
número pero con las cifras invertidas de como resultado 72. Dar como respuesta la
suma de sus cifras.
10. Si al numeral 1432 se le quita la cifra del tercer orden y se le reemplaza por la cifra
a, el número resultante es mayor que el anterior en 200 unidades. Hallar el valor de a.
DEMUESTRA LO APRENDIDO
7. Hallar un número de dos cifras, ambas diferentes de cero, tal que al restarle el mismo
número pero con las cifras invertidas dé como resultado 63. Además se sabe que la
suma de las dos cifras es 9. Dar como respuesta el producto de las cifras del número
perdido.
COLEGIO TRILCE Página 7

8. ARITMETICA
8. Se tiene un número de tres cifras al cual se le agrega un 7 al final; luego al mismo
número original se le agrega un 7 al comienzo. Si se suman los dos números de
cuatro cifras se obtiene 9768. Hallar la suma de las cifras del número original.
9. A un número de dos cifras se le agregan dos ceros a la derecha, aumentándose el
número en 4752 unidades. Calcular el número original.
10. Hallar un número de dos cifras, cuya suma de cifras es 10 y tal que al invertir el orden
de sus cifras, el número disminuye en 36 unidades. Dar como respuesta el producto de
las cifras del número pedido.
DESAFÍO
Un número está compuesto por tres cifras, la cifra de las centenas es cuatro veces la cifra de las
unidades y la cifra de las decenas es igual a la mitad de la suma de las otras cifras. Dar como respuesta el
producto de las cifras de dicho número.
P a r a e s t e s e g u n d o t e m a , q u e r id o s a l u m n o s ,
e s t u d ia r e m o s o t r o s s is t e m a s d e n u m e r a c ió n ;
p a r a lo c u a l, g e n e r a liz a r e m o s a lg u n o s
c o n c e p t o s d a d o s e n e l t e m a a n t e r io r.
1. Base de un Sistema de Numeración:
Es la cantidad de unidades requeridas de un orden cualquiera para formar una unidad
de un orden inmediato superior.
Así; por ejemplo, si deseo representar un grupo de unidades en base 7, necesito
grupos de siete unidades para ser agrupados y formar una unidad de orden inmediato
superior.
COLEGIO TRILCE Página 8

9. ARITMETICA
Al agrupar de 7 en 7, se han formado cuatro grupos y han
quedado sin agrupar seis unidades, luego se puede
decir que dicha agrupación tiene la forma siguiente:
46
(7)
Otro ejemplo: Agrupar 26 unidades en base 3.
La agrupación es:
2 grupos de 3 × 3 = 2 × 3
2
2 grupos de 1 × 3 = 2 × 3
1
2 unidades sueltas = 2
o también: 222
(3)
.
Condiciones de la base:
a) La base de un sistema de numeración siempre es un número natural mayor que 1.
b) La menor agrupación que se puede hacer es dos unidades, por lo que la menor
base es 2 (Sistema Binario).
2. Principios fundamentales de los Sistemas de Numeración:
2.1 Toda cifra de un numeral es menor que su base y utiliza n cifras: el cero y (n -
1) cifras significativas.
0
c e r o
1 ; 2 ; 3 ; 4 ; . . . ; ( n - 1 );
c if r a s s ig n if ic a t iv a s
Ejemplo:
COLEGIO TRILCE Página 9

10. ARITMETICA
- 1023
(5)
→ Todas las cifras son menores que la base 5, entonces,
el número 10 está correctamente escrito.
- 222222
(3)
→ Todas las cifras son menores que la base 3.
- 86577
(8)
→ Todas las cifras no son menores que la base 8, la cifra
que ocupa el primer lugar (el 8) no es menor que 8,
entonces el número no está correctamente
representado.
Entonces de los ejemplos, afirmamos lo siguiente:
En la base b:
- Se usan b cifras para formar un orden inmediatamente superior cualquiera.
- Las cifras pueden ser:
Significativas = {1; 2; 3; 4; ...; (b - 1))
C if r a m á x i m a
No significativa o auxiliar: 0 (cero)
Conclusión: Cifra Base
Principales Sistemas de Numeración
COLEGIO TRILCE Página 10

11. ARITMETICA
B a s e S i s t e m a s d e N u m e r a c i ó n C i f r a s d i f e r e n t e s q u e u t i l i z a
2
3
4
5
6
7
8
9
1 0
1 1
1 2
B in a r io o d u a l
T e r n a r io
C u a t e r n a r io
Q u in a r io
S e n a r io
H e p t a n a r io
O c t a n a r io
N o n a r io
D e n a r io o d e c im a l
U n d e c im a l
D u o d e c im a l
0 ; 1
0 ; 1 ; 2
0 ; 1 ; 2 ; 3
0 ; 1 ; 2 ; 3 ; 4
0 ; 1 ; 2 ; 3 ; 4 ; 5
0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6
0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7
0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8
0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9
0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ;
0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; ;
Para representar numerales con cifras mayores que 9, se toma en cuenta:
α = 10; β = 11; γ = 12; etc.
Como consecuencia del cuadro anterior, existen infinitos sistemas de numeración.
3. Descomposición polinómica de un número en cualquier Sistema de
Numeración
abcd
(n)
= a × n
3
+ b × n
2
+ c × n + d
Ejemplos:
• 1234
(5)
= 1 × 5
3
+ 2 × 5
2
+ 3 × 5 + 4 = 125 + 50 + 15 + 4 = 194
•
(9)
= a × 9
2
+ a × 9 + a = 81a + 9a + a = 91a
•
(a)
= 3 × a
2
+ 4 × a + 0 = 3a
2
+ 4a
COLEGIO TRILCE Página 11

12. ARITMETICA
COLEGIO TRILCE Página 12

13. ARITMETICA
DEMUESTRA LO APRENDIDO
DESAFÍO
Un número consta de 2 cifras, cuya suma es 11. Si intercambiamos el orden de sus
cifras resulta un número que excede en 5 al triple del número original. Hallar dicho
número.
a. 47 b. 29 c. 65 d. 83 e. 56
COLEGIO TRILCE Página 13

14. ARITMETICA
Consiste en transformar un número de cierto sistema de numeración a otro sistema de
numeración, pero sin dejar de representar estos números la misma cantidad de unidades.
También se le conoce a este tema como cambio de base.
Caso I: De una base diferente de 10 a la base 10
Para este caso se utiliza el procedimiento de descomposición polinómica, efectuando
para ello las operaciones indicadas.
Descomposición polinómica: )n(abc
= a × n
2
+ b × n + c
Ejemplos:
•
 2734241123
816
2
)4( =+×+×= 
•
 71769798879
63648
2
)9( =+×+×= 
•
 b8a65a8b8aaba
b8a64
2
)8( +=+×+×= 
También se puede utilizar el método de Ruffini, así:
E n e l s is t e m a d e c im a l
4
1 2
+
4
6
3
+
2 4
2 7
×
×
1
COLEGIO TRILCE Página 14

15. ARITMETICA
E n e l s is t e m a d e c im a l
9
1
8
7
+
7 2
7 9
6
+
7 1 1
7 1 7
×
×
Caso II: De base 10 a una base diferente de 10
Se utiliza el método de divisiones sucesivas, que consiste en dividir el número dado del
sistema decimal (base 10) entre la base n a la cual se desea convertir; si el cociente es
mayor que n, se dividirá nuevamente y así en forma sucesiva hasta que se llegue a una
división donde el cociente sea menor que n. Luego, se toma el último cociente y los
residuos de todas las divisiones, desde el último residuo hacia el primero y este será el
número expresado en base n.
Ejemplo:
• Convertir 25 a base 8:
2 5 8
1 3 2 5 = 3 1 ( 8 )
• Convertir 100 a base 3:
1 0 0 3
1 3 3 3
0 1 1 3
2 3 3
0 1
1 0 0 = 1 0 2 0 1 ( 3 )
• Convertir 216 a base 6:
2 1 6 6
0 3 6 6
0 6 6
0 1
2 1 6 = 1 0 0 0 ( 6 )
COLEGIO TRILCE Página 15

16. ARITMETICA
Caso III: De una base diferente de 10 a otra diferente de 10
Se utilizan en este caso, los dos métodos vistos anteriormente, es decir, primero
llevamos el número de base diferente de 10, por descomposición polinómica, al
sistema decimal; y, luego este número, por divisiones sucesivas, lo llevamos al otro
sistema de base diferente a 10.
Ejemplos:
1. Convertir: 543
(6)
a base 4
a. Descomposición polinómica:
 20736465543
24180
2
)6( =+×+×= 
b. Divisiones sucesivas:
2 0 7 4
3 5 1 4
3 1 2 4
0 3
L u e g o : 5 4 3 = 2 0 7 = 3 0 3 3 ( 4 )( 6 )
2. Convertir: 2134
(5)
a base nueve
a. Descomposición polinómica:
 29445351522134
1525
2
250
3
)5( =+×+×+×= 
b. Divisiones sucesivas:
2 9 4 9
6 3 2 9
5 3
L u e g o : 2 1 3 4 = 2 9 4 = 3 5 6( 5 ) ( 9 )
PROPIEDAD: En un numeral que representa la misma cantidad de unidades simples
en dos sistemas de numeración diferentes, deberá cumplirse que donde tenga mayor
COLEGIO TRILCE Página 16

17. ARITMETICA
representación aparente le corresponde una menor base y viceversa, a menor
representación mayor base.
N = R A T Ó N = P A V O( x ) ( y )
+
+
Ejemplo:
N u m e r a l m e n o r
1 3 4 = 2 5 1 = 2 0 1 2( 7 ) ( 4 )
N u m e r a l m a y o r
M a y o r b a s e M e n o r b a s e
¡ LISTOS … A TRABAJAR ¡
1. Convertir al sistema decimal:
a. 1101
(2)
b. 320
(4)
c. 1032
(5)
d. 2031
(4)
e. 132
(9)
2. Convertir:
a. 123 al sistema binario. b. 871 al sistema ternario.
c. 2031 al sistema quinario. d. 952 al sistema undecimal.
e. 642 al sistema de base 15.
3. Convetir:
a. 1002
(3)
al sistema quinario. b. 432
(7)
a base 4.
c. 2134
(5)
al sistema nonario. d. 1023
(4)
a base 6.
e. 123
(4)
al sistema octanario.
COLEGIO TRILCE Página 17

18. ARITMETICA
4. Hallar a + b + c si: 1230
(5)
= )7(abc
a. 8 b. 9 c. 10 d. 11 e. 12
5. Convertir: )4(
)2a)(1a)(1a( −−+
al sistema senario. Dar como respuesta la suma de
sus cifras.
a. 4 b. 5 c. 6 d. 7 e. 8
DEMUESTRA LO APRENDIDO
COLEGIO TRILCE Página 18

19. ARITMETICA
LISTOS … A TRABAJAR
1. Hallar el valor de A + B + C, si se sabe que:
COLEGIO TRILCE Página 19

20. ARITMETICA
A: es el mayor número de tres cifras.
B: es el mayor número impar de dos cifras diferentes.
C: es el mayor número de tres cifras diferentes.
a. 2063 b. 2073 c. 2083 d. 2093 e. 3113
2. ¿Cuál es el menor número cuyas cifras suman 24? Dar como respuesta su cifra de
mayor orden.
a. 6 b. 7 c. 8 d. 9 e. 10
3. Hallar un número de tres cifras que cumpla las condiciones siguientes para sus cifras:
I. La primera es el doble de la tercera.
II. La segunda es el triple de la primera.
Dar como respuesta la suma de sus cifras.
a. 6 b. 7 c. 8 d. 9 e. 10
4. Si el numeral )a3)(5a)(1b(b)1a( −++− es capicúa. Hallar la cifra de tercer orden.
a. 6 b. 7 c. 8 d. 9 e. 10
5. Si los numerales están correctamente escritos. Calcular a + b
I. )5()2a)(a2( −
II. )9(
)5b(
3
b
+





a. 3 b. 4 c. 5 d. 6 e. 7
6. ¿Cuántas numerales de dos cifras cumplen que son iguales a cuatro veces la suma
de sus cifras?
a. 2 b. 3 c. 4 d. 5 e. 6
7. Un número de dos cifras es igual a la suma de siete veces la cifra de decenas más
nueve veces la cifra de las unidades. ¿cuál es la suma de sus cifras?
COLEGIO TRILCE Página 20

21. ARITMETICA
a. 9 b. 10 c. 11 d. 12 e. 13
8. Al menor número de tres cifras diferentes de la base nueve, convertirlo al sistema
senario. Dar como respuesta la suma de sus cifras.
a. 6 b. 7 c. 8 d. 9 e. 10
9. Hallar: a + b + c.
Si: )9()8( 256)2c)(1b)(2a( =−+−
a. 8 b. 9 c. 10 d. 12 e. 13
10. Si se cumple: )2()3( abcde201 =
;
hallar: a + b + c + d + e + n
a. 3 b. 4 c. 5 d. 6 e. 7
DEMUESTRA LO APRENDIDO
1. Hallar el valor de A + B + C, si se sabe que:
A: Es el menor número de tres cifras diferentes.
B: Es el mayor número par de dos cifras diferentes.
C: Es el menor número de tres cifras.
a. 280 b. 290 c. 300 d. 310 e. 320
2. ¿Cuál es el menor número cuya cifras suman 30? Dar como respuesta la cifra de
mayor orden.
a. 6 b. 7 c. 8 d. 9 e. 10
3. Hallar un número de tres cifras que cumpla las condiciones siguientes para sus cifras:
I. La primera es el triple de la tercera.
II. La segunda es el doble de la primera.
COLEGIO TRILCE Página 21

22. ARITMETICA
a. 7 b. 8 c. 9 d. 10 e. 11
4. Si el numeral )x6)(1x)(3y)(2x( −++− es capicúa. Hallar la cifra de segundo orden.
a. 3 b. 4 c. 5 d. 6 e. 7
5. Si los numerales están correctamente escritos. Calcular x + y.
I. )7(
)1x(
3
x
)x2( +





II. )8(
)3y)(2y(
2
y
−+





a. 4 b. 5 c. 6 d. 7 e. 8
6. ¿Cuántos numerales de dos cifras cumplen que son iguales a siete veces la suma de
sus cifras?
a. 2 b. 3 c. 4 d. 5 e. 6
7. Si: (n - 1)(n
3
)(n + 3) = aba
(7)
; calcular: a + b + n.
a. 7 b. 8 c. 9 d. 10 e. 11
8. Hallar: a + b + c + d + n; si se cumple: )n()3( abcd102 =
a. 3 b. 4 c. 5 d. 6 e. 7
9. Convertir el mayor numeral de 3 cifras diferentes de la base 5 al sistema octanario.
a. 10 b. 11 c. 12 d. 13 e. 14
10. Convertir el menor numeral de 4 cifras diferentes del sistema senario al sistema
nonario. Dar como respuesta la suma de sus cifras.
a. 12 b. 13 c. 14 d. 15 e. 16
DESAFÍO
COLEGIO TRILCE Página 22

23. ARITMETICA
Al convertir el mayor numeral de 3 cifras diferentes del sistema senario al sistema
cuaternario se obtiene: abcd . Hallar: a + b + c + d
a. 6 b. 7 c. 8 d. 9 e. 10
1. MÚLTIPLOS
Un número entero A es múltiplo de otro entero B, si A contiene a B una
cantidad exacta de veces.
Ejemplo 1: Averiguar si 72 es múltiplo de 6.
Veamos:
Para obtener 72 se necesita 12 veces el valor de 6, entonces: 72 = 6(12)
∴ 72 es múltiplo de 6.
Ejemplo 2: Averiguar si 143 es múltiplo de 11.
Veamos:
Para obtener 143 necesito 13 veces el valor de 11, entonces 143 = 11(13)
∴ 143 es múltiplo de 11.
Ejemplo 3: Escribe los 10 primeros enteros positivos múltiplos de 4.
Solución:
1 × 4; 2 × 4; 3 × 4; 4 × 4; 5 × 4; 6 × 4; 7 × 4; 8 × 4; 9 × 4; 10 × 4
luego: 4; 8; 12; 16; 20; 24; 28; 32; 36; 40.
2. DIVISOR DE UN NÚMERO
Es el número que está contenido en el primero una cantidad exacta de veces,
también se le conoce como submúltiplos.
Ejemplo 1:
* 4 es submúltiplo de 24 porque está contenido en 24 seis veces.
COLEGIO TRILCE Página 23

24. ARITMETICA
* 8 es factor de 64 porque está contenido en 64 ochos veces.
Ejemplo 2: Halla los divisores de 24.
Solución:
D(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ejemplo 3: ¿Cuántos divisores más tiene 45 que 13?
Solución:
D(45) = {1; 2; 3; 5; 9; 15; 45} µ tiene 6 divisores
D(13) = {1; 13} µ tiene 2 divisores
Respuesta: 45 tiene 4 divisores más que 13.
Observación:
En el campo numérico de los enteros Z, los múltiplos pueden ser negativos, además
del 0, así por ejemplo:
* Los múltiplos de 15 son:
1 5 = 1 5 k
1 5 ( 1 ) ; 1 5 ( 2 ) ; 1 5 ( 3 ) ; 1 5 ( 4 ) ; . . . . .
1 5 ( 0 ) = c e r o
1 5 ( - 1 ) ; 1 5 ( - 2 ) ; 1 5 ( - 3 ) ; 1 5 ( - 4 ) ; . . . .
º
donde k es un entero cualquiera.
De todo esto podemos afirmar lo siguiente:
i. Todo número tiene INFINITOS múltiplos.
ii. El CERO es múltiplo de todos los números.
COLEGIO TRILCE Página 24

25. ARITMETICA
A B
m ú lt ip lo d e
d iv is ib le p o r
f a c t o r d e
d iv is o r d e
I I . E j m . :
1 2
m ú lt ip lo d e
d iv is ib le p o r
f a c t o r d e
d iv is o r d e
3
I . A = B
s e le e : A e s m ú lt ip lo d e B
º
E n r e s u m e n :
3. NÚMEROS PRIMOS
Llamados tambien PRIMOS ABSOLUTOS, son aquellos números que tienen
unicamente dos divisores que son la unidad y el mismo número.
Ejemplos:
Número PrimoDivisores
2 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
3 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
5 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
7 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
11 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
4. NÚMEROS COMPUESTOS
Son aquellos números que tienen más de dos divisores.
Número Compuesto Divisores
4 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
COLEGIO TRILCE Página 25

26. ARITMETICA
6 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
8 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
10 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
12 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
TABLA DE LOS NÚMEROS PRIMOS MENORES QUE 100
(Criba de Eratóstenes)
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
Entonces: Los números primos menores que 100 son:
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
• Propiedades
1. El uno no es un número primo. sólo tiene un divisor, es considerado como
número simple.
2. Los números primos son infinitos.
3. El dos es el único número primo par.
4. El dos y el tres son los únicos números consecutivos y a la vez primos
absolutos
5. NÚMEROS PRIMOS ENTRE SI (PESI)
COLEGIO TRILCE Página 26

27. ARITMETICA
Dos o más números son primos entre si (PESI), cuando tienen como único divisor
común a la unidad.
• Ejemplo: ¿6, 14 y 9 son números PESI?
veamos:
Divisores
6 : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
14 : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
9 : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Se observa que _________, es el único divisor común a dichos números
Entonces: ______________ son números ______________.
• Ejemplo: ¿21, 15 y 8 son números PESI?
veamos:
Divisores
21 : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
15 : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
8 : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Se observa que: __________, es el único divisor común a dichos números.
Entonces: ______________ son números ______________.
• Ejemplo: ¿8, 6 y 14 son números PESI?
veamos:
Divisores
8 : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
6 : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
14 : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Se observa que: __________, son divisores comunes a dichos números.
Entonces: ______________ no son números ______________.
• Ejemplo: ¿10, 35 y 15 son números PESI?
COLEGIO TRILCE Página 27

28. ARITMETICA
veamos:
Divisores
10 : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
35 : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
15 : _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Se observa que: __________, son divisores comunes a dichos números.
Entonces: ______________ no son números ______________.
Propiedades
1. Dos o más números consecutivos son siempre números PESI.
2. Dos o más números impares consecutivos son siempre números PESI.
6. DESCOMPOSICIÓN CANÓNICA (DC)
Todo número compuesto se puede expresar como el producto de sus divisores
primos diferentes elevados a exponentes enteros positivos.
• Ejemplo: Hallar la descomposición canónica de 18.
V e a m o s : 1 8
E n t o n c e s : 1 8 = _ _ _ _ _ _ _ _ _ _ _ _ _
• Ejemplo: Hallar la descomposición canónica de 120.
V e a m o s : 1 2 0
E n t o n c e s : 1 2 0 = _ _ _ _ _ _ _ _ _ _ _ _ _
Nota: Los divisores primos de un número compuesto se observan en su
descomposición canónica.
COLEGIO TRILCE Página 28

29. ARITMETICA
7. CANTIDAD DE DIVISORES (CD)
Sea N un número compuesto cuya descomposición canónica es:
N = a . b . cm n p
d o n d e :
a ; b y c
m ; n y p
:
:
f a c t o r e s p r im o s a b s o lu t o s
e x p o n e n t e s e n t e r o s p o s it iv o s
Entonces: la cantidad de divisores de N será:
C D ( N ) = ( m + 1 ) ( n + 1 ) ( p + 1 )
• Ejemplo: Hallar la cantidad de divisores de 180.
V e a m o s : 1 8 0
L u e g o :
F i n a lm e n t e :
1 8 0 = _ _ _ _ _ _ _ _ _ _ _ _ _
C D = _ _ _ _ _ _ _ _ _ _ _ _ _( 1 8 0 )
= _ _ _ _ _ _ _ _ _ _ _ _ _
= _ _ _ _ _ _ _ _ _ _ _ _ _
• Ejemplo: Hallar la cantidad de divisores de 480.
El primer paso es hallar la descomposición canónica de 480.
COLEGIO TRILCE Página 29

30. ARITMETICA
V e a m o s : 4 8 0
L u e g o :
F in a lm e n t e :
4 8 0 = _ _ _ _ _ _ _ _ _ _ _ _ _
C D = _ _ _ _ _ _ _ _ _ _ _ _ _( 4 8 0 )
= _ _ _ _ _ _ _ _ _ _ _ _ _
= _ _ _ _ _ _ _ _ _ _ _ _ _
¡LISTOS… A TRABAJAR ¡
1. a. ¿Cuál es el menor número primo mayor que 25?
b. ¿Cuál es el mayor número primo menor que 52?
2. ¿Cuáles son los números primos que sumados de 2 en 2 dan 100 como resultado?
3. Hallar a + b; si:
a = mayor número primo menor que 70
b = menor número primo mayor que 20
4. ¿Cuál es el menor número compuesto de 2 cifras?
5. ¿Cuál es el mayor número compuesto de 2 cifras?
6. Indicar verdadero V o falso F, según convenga:
a. 35 = 5 ( )
b. 8 = 16 ( )
c. 111 = 37 ( )
d. 53 = 7 ( )
COLEGIO TRILCE Página 30

31. ARITMETICA
e. 26 = 13 ( )
7. ¿Cuál es la suma de cifras del mayor múltiplo de 13 de dos cifras?
8. Si el número 2a5 es múltiplo de 8, ¿cuántos valores puede tener a?
9. Hallar la suma de las partes alícuotas de 12.
10. Si: A = {x/x ∈ N, x es divisor de 14} y
B = {x/x ∈ N, x es divisor de 8}
hallar:
a. A ∪ B b. A ∩ B c. A - B
DEMUESTRA LO APRENDIDO
1. ¿Cuál es el menor número compuesto mayor que 20?
2. Hallar la suma de todos los números compuestos mayores que 12 pero menores que
23?
3. ¿Qué grupo de números son PESI?
a. 8; 25; 32 b. 9; 27; 35 c. 18; 30; 43
4. Hallar la descomposición canónica en cada caso:
a. 220 b. 280 c. 390 d.
600
5. Hallar la cantidad de divisores de:
a. 340 b. 420
6. ¿Cuántos números de dos cifras son 5?
7. Del 1 al 100, ¿cuántos números son 7?
COLEGIO TRILCE Página 31

32. ARITMETICA
8. Si el siguiente número: x453 es divisible por 7, calcular el valor de x.
9. Del 1 al 80, ¿cuántos números son 3?
10. Si: a 10, hallar la suma de valores que puede tomar en: 3a + 1 = 7.
DESAFÍO
Hallar la cantidad de divisores de: 3
2
×××× 75
COLEGIO TRILCE Página 32

33. ARITMETICA
COLEGIO TRILCE Página 33

34. ARITMETICA
COLEGIO TRILCE Página 34

35. ARITMETICA
COLEGIO TRILCE Página 35

36. ARITMETICA
COLEGIO TRILCE Página 36

37. ARITMETICA
COLEGIO TRILCE Página 37

38. ARITMETICA
COLEGIO TRILCE Página 38

39. ARITMETICA
DESAFÍO
DESAFIO
En un juego infantil se va contando de 1 a 100 y se aplaude cada vez que se dice un
múltiplo de 3 o un número que termina en 3. ¿Cuántas veces se has aplaudido al
terminar el juego?
a. 30 b.33 c.36 d.39 e.43
E l m é t o d o d e o b t e n c ió n d e l m á x im o c o m ú n d iv is o r
p o r d iv is io n e s s u c e s iv a s , a p a r e c e y a d e s c r it o e n e l
s ig lo I V ( a . C .) e n la o b r a E le m e n t o s , d e l m a t e m á t ic o
g r ie g o E u c li d e s . E n d ic h a o b r a t a m b ié n s e p r o p o n ía u n
m é t o d o p a r t a o b t e n e r e l m ín im o c o m ú n m ú lt ip lo .
¿ S a b ía s q u é ?
COLEGIO TRILCE Página 39

40. ARITMETICA
MÁXIMO COMÚN DIVISOR
(m.c.d)
I. DEFINICIÓN
Es el mayor de los divisores comunes que presentan dos o más números enteros
positivos.
Ejemplo: Sean los números 8 y 12.
D = { 1 ; 2 ; 4 ; 8 }8
D = { 1 ; 2 ; 3 ; 4 ; 6 ; 1 2 }1 2
Los divisores comunes son: _ _ _ _ _ _ _ _ _ _ _ _
El mayor divisor común es: _ _ _ _ _ _ _ _ _ _ _ _
Entonces el m.c.d.(8;12) = _ _ _ _ _ _ _ _ _ _ _ _
II. Método para hallar el m.c.d.
P O R D E S C O M P O S I C I Ó N S I M U L T Á N E A
S e e x t r a e d e lo s n ú m e r o s t o d o s lo s
f a c t o r e s c o m u n e s h a s t a o b t e n e r
n ú m e r o s P E S I , lu e g o e l m . c . d . d e
d ic h o s n ú m e r o s e s e l p r o d u c t o d e
lo s f a c t o r e s e x t r a íd o s .
E j e m p lo :
8
4
2
-
-
-
1 2
6
3
2
2
m . c . d . = 2 × 2 = 4
COLEGIO TRILCE Página 40

41. ARITMETICA
P O R D E S C O M P O S I C I Ó N C A N Ó N I C A
A lo s n ú m e r o s s e le s d e s c o m p o n e
c a n ó n ic a m e n t e , lu e g o e l m . c . d . d e
d ic h o s n ú m e r o s e s e l p r o d u c t o d e
t o d o s s u s d iv is o r e s p r im o s c o m u n e s
e le v a d o s a s u m e n o r e x p o n e n t e .
E j e m p lo :
8
4
2
1
2
2
2
e n t o n c e s e l m . c . d . ( 8 ; 1 2 ) = 2 = 42
1 2
6
3
1
2
2
3
lu e g o : 8 = 2 3
1 2 = 2 2
× = 3
¡ LISTOS … A TRABAJAR ¡
1. Completa el siguiente cuadro:
N ú m e r o D i v i s o r e s
3 6
2 4
4 0
D i v i s o r e sN ú m e r o
2 7
1 8
3 0
Ahora completa el siguiente cuadro:
N ú m e r o
1 8 y 2 4
3 0 y 4 0
1 8 y 2 7
2 4 y 3 6
D i v i s o r e s c o m u n e s m . c . d .
2. Hallar el m.c.d. por descomposición simultánea en cada caso:
a . 4 9 y 6 3
-
m . c . d . =
b . 4 8 y 7 2
-
m . c . d . =
c . 9 0 y 1 2 0
-
m . c . d . =
COLEGIO TRILCE Página 41

42. ARITMETICA
3. Hallar el mc.d. por descomposición canónica, en cada caso:
a. 52 y 78 b. 56 y 72 c. 84 y 96
4. Hallar el m.c.d. si:
A = 2
2
× 3
4
× 5
B = 2
2
× 15
m.c.d.(A;B) =
DEMUESTRA LO APRENDIDO
1. Hallar el mc.d. por descomposición simultánea, en cada caso:
a. 45 y 95 b. 75 y 125 c. 24; 36 y 68
d. 30; 60 y 90 e. 20; 36 y 40 f. 18 y 15
2. Hallar el mc.d. por descomposición canónica, en cada caso:
a. 64 y 96 b. 160 y 180 c. 30; 60 y 72
d. 48; 52 y 72 e. 50; 300 y 600 f. 48 y 36
3. Hallar el mc.d. de A, B y C; si:
A = 3
3
× 5
4
× 8
B = 12 × 27
C = 25 × 36
COLEGIO TRILCE Página 42

43. ARITMETICA
DESAFÍO
• Hallar el m.c.d. de: 5 y 9. ¿Qué ocurrió?
• ¿Por qué no se estudia el mínimo común divisor?
MÍNIMO COMÚN MÚLTIPLO
(m.c.m)
I. DEFINICIÓN
Es el menor de los múltiplos comunes que presentan dos o más números enteros
positivos diferentes de 0.
Ejemplo: Sean los números 4 y 6.
4 = 0 ; 4 ; 8 ; 1 2 ; 1 6 ; 2 0 . . .
º
6 = 0 ; 6 ; 1 2 ; 1 8 ; 2 4 ; 3 0 . . .
º
Los múltiplos comunes son: _ _ _ _ _ _ _ _ _ _ _ _
El menor múltiplo común es: _ _ _ _ _ _ _ _ _ _ _ _
Entonces el m.c.m.(4;6) = _ _ _ _ _ _ _ _ _ _ _ _
II. Métodos para hallar el m.c.m.
P O R D E S C O M P O S I C I Ó N S I M U L T Á N E A
S e e x t r a e n d e lo s n ú m e r o s t o d o s lo s
f a c t o r e s c o m u n e s y n o c o m u n e s h a s t a
o b t e n e r la u n id a d e n c a d a n ú m e r o ;
lu e g o , e l m c . m . d e d ic h o s n ú m e r o s e s
e l p r o d u c t o d e lo s f a c t o r e s e x t r a íd o s .
E j e m p lo :
4
2
1
1
-
-
-
-
6
3
3
1
2
2
3
m . c . m . ( 4 ; 6 ) = 2 × 2 × 3 = 1 2
COLEGIO TRILCE Página 43

44. ARITMETICA
P O R D E S C O M P O S I C I Ó N C A N Ó N I C A
A lo s n ú m e r o s s e le s d e s c o m p o n e
c a n ó n ic a m e n t e ; lu e g o , e l m . c . m . d e
d ic h o s n ú m e r o s e s e l p r o d u c t o d e
t o d o s lo s d iv is o r e s p r im o s c o m u n e s
y n o c o m u n e s e le v a d o s a s u m a y o r
e x p o n e n t e .
E j e m p lo :
4
2
1
2
2
e n t o n c e s e l m . c . m . = 2 × 32
6
3
1
2
3
lu e g o : 4 = 2 2
6 = 2 × 3
¡ LISTOS … A TRABAJAR ¡
1. Completa el siguiente cuadro:
N ú m e r o M ú l t i p l o s ( 1 0 p r i m e r o s )
8
1 0
1 2
M ú l t i p l o s ( 1 0 p r i m e r o s )N ú m e r o
1 5
1 6
2 0
Ahora completa el siguiente cuadro:
N ú m e r o
8 y 1 2
1 0 y 1 5
8 y 2 0
1 6 y 2 0
M ú l t i p l o s c o m u n e s m . c . m .
2. Hallar el m.c.m. por descomposición simultánea, en cada caso:
COLEGIO TRILCE Página 44

45. ARITMETICA
a . 3 0 y 4 5
-
m . c . m . =
b . 1 2 ; 1 5 y 2 0
-
m . c . m . =
c . 4 2 ; 3 6 y 4 8
-
m . c . m . =
3. Hallar el m.c.m. por descomposición canónica, en cada caso:
a. 45; 75 y 90 b. 12; 14 y 16 c. 9 y 15
4. Hallar el m.c.m. de A y B; si:
A = 2
3
× 3
2
× 5
3
B = 2
6
× 3 × 5
2
DEMUESTRA LO APRENDIDO
1. Hallar el m.c.m. por descomposición simultánea, en cada caso:
a. 35 y 63 b. 12 y 60 c. 15 y 25
d. 24 y 36 e. 9 y 15 e. 120; 148 y 200
2. Hallar el m.c.m. por descomposición canónica, en cada caso:
COLEGIO TRILCE Página 45

46. ARITMETICA
a. 85 y 30 b. 36 y 99 c. 96 y 100
d. 24 y 30 e. 200; 300 y 400 e. 160; 180 y 360
3. Hallar el m.c.m. de P, Q y R; si:
P = 3
2
× 5
3
× 7
2
Q = 2 × 3
3
× 5
2
× 7
R = 3
2
× 7
DESAFÍO
• Hallar el m.c.m. de 0 y 4. ¿Qué sucede?
• ¿Se podrá hallar el máximo común múltiplo de dos números?
COLEGIO TRILCE Página 46

47. ARITMETICA
P a r a p o d e r r e s o lv e r p r o b le m a s s o b r e e l m . c . m . y e l
m . c . d . d e b e s t e n e r e n c u e n t a la s s ig u ie n t e s in d ic a c io n e s :
¿ S a b ía s q u é ?
1 º D e b e s le e r e l p r o b le m a la s v e c e s q u e s e a n n e c e s a r ia s .
2 º S e d e b e r e c o g e r lo s d a t o s d e l p r o b le m a .
3 º I d e n t if ic a r lo q u e s e s o lic it a .
4 º P la n t e a r e s t r a t e g ia s a l p r o b le m a .
5 º C o m p r o b a r la s e s t r a t e g ia s y e le g ir u n a d e e lla s .
¡ LISTOS .,.. A TRABAJAR ¡
1. Tres compañías de navegación pasan por cierto puerto. La primera cada 8 días; la
segunda cada 18 días y la tercera cada 21 días. ¿Cada cuántos días se hallan los
buques de los tres compañías simultáneamente en este puerto?
2. Tres aviones salen de una misma ciudad con una periodicidad de 4 días; 5 días y 10
días, respectivamente. Si la última vez que salieron juntos fue el 14 de julio, ¿cuál
será la próxima fecha en que volverán a salir juntos?
COLEGIO TRILCE Página 47
DATOS SOLUCION
DATOS SOLUCION

48. ARITMETICA
3. ¿Cuál es la menor longitud que debe tener una varilla para que se puede dividir en
trozos de 24 cm; 27 cm; ó 45 cm de longitud sin que sobre ni falte nada?
4. Dos ciclistas dan vueltas en una pista; el primero cada 48 segundos y el segundo
cada 64 segundos. Si salen juntos, ¿al cabo de cuánto tiempo pasarán por el sitio de
partida?
5. Tres perros salen juntos en una carrera. El primero tarda 20 segundos en dar la
vuelta a la pista, el segundo tarda 33 segundos y el tercero, 36 segundos. ¿Al cabo
de cuántos segundos volverán a pasar juntos por la línea de salida, si salen juntos?
COLEGIO TRILCE Página 48
DATOS SOLUCION
DATOS SOLUCION
SOLUCIONDATOS

49. ARITMETICA
6. Dos cintas de 12 metros y 16 metros de longitud se quieren dividir en pedazos iguales
y de la mayor longitud posible. ¿Cuál será la longitud de cada pedazo?
7. ¿Cuál es la mayor longitud de una regla con la que se puede medir exactamente 3
cintas de 120 cm; 180 cm y 240 cm?
8. Se desean dividir dos cordeles de 60 y 80 metros de longitud posible. ¿Cuál será la
longitud de cada trozo resultante?
COLEGIO TRILCE Página 49
DATOS SOLUCION
DATOS SOLUCION
DATOS SOLUCION

50. ARITMETICA
9. Se tienen que envasar 120 kg; 144 kg y 200 kg de plomo en tres cajas de modo que
los bloques de cada una tenga el mismo peso y el mayor posible. ¿Cuánto pesa cada
pedazo de plomo?
10. ¿Cuál es el mayor número que puede dividir a la vez 612; 2040 y 8976?
COLEGIO TRILCE Página 50
DATOS SOLUCION
SOLUCIONDATOS

51. ARITMETICA
DEMUESTRA LO APRENDIDO
1. ¿Cuál es el mayor número de niños entre los cuales hay que repartir 12; 24 y 60
panes simultáneamente para que, en cualquiera de los casos, cada uno reciba la
misma cantidad?
2. Se tiene tres cubos de 84 cm
3
; 270 cm
3
y 330 cm
3
. ¿Cuál es el mayor volumen en
cm
3
que cabe un número exacto de veces en cada uno de ellos?
3. ¿Cuál es el menor número de caramelos que se puede repartir simultáneamente
entre 15 y 20 niñas para que en cada caso una niña reciba una cantidad exacta?
4. En una competencia automovilística de circuito cerrado, tres automóviles arrancan
juntos. Si tardan 10; 12 y 15 minutos en dar una vuelta completa. ¿Al cabo de qué
tiempo pasarán juntos por la línea de partida?
5. ¿Cuál será la mayor longitud de una medida con la que se puede medir exactamente
tres dimensiones 280; 1120 y 16000 metros?
6. Un tren sale cada 5 horas, otro tren sale cada 3 horas, si han salido al mismo tiempo,
a las 9 de la mañana. ¿Cuánto volverán a coincidir?
COLEGIO TRILCE Página 51

52. ARITMETICA
7. Una puerta se abre cada 20 segundos, otra cada 12 segundos y una tercera cada 30
segundos, si se abren simultáneamente a las 12 del día. ¿A qué hora vuelven a
abrirse simultáneamente?
8. ¿Cuál es la menor distancia que se puede medir exactamente con una regla de 30
cm, 40 cm ó de 50 cm?
9. Hallar el mayor número de niños entre los que se puede repartir, en partes iguales,
174 soles y 730 soles.
10. Una madre distribuye exactamente por partes iguales entre sus hijos: 90
caramelos y 75 chocolates. ¿Qué número de cada dulce corresponde a cada uno de
ellos?
DESAFÍO
Hallar la menor cantidad de soles que hay que repartir entre 5, 6, 9 y 13 niños, de tal manera que en
cada caso sobren 4 soles.
SISTEMA DE NUMERACIÓN DECIMAL
1. En: ;273abc = hallar el V.A.(c) + V.R.(a) - V.A.(b)
2. Indicar la suma de la cifra del segundo orden más la cifra del quinto orden en:
956 783
3. Indicar la suma de la cifra del primer lugar más la cifra del cuarto lugar en:
9 128 751
4. Si se cumple que: )a2(15 es el cuadruple de )a3(3 . Calcular el valor de a.
COLEGIO TRILCE Página 52

53. ARITMETICA
5. Hallar un número de dos cifras, ambas diferentes de cero, tal que al restarle el mismo
número pero con las cifras invertidas, dé como resultado 27. Si se sabe que la suma
de las dos cifras es 13.
TRANSFORMACIÓN DE SISTEMA DE NUMERACIÓN
6. Convertir: 15042
(6)
a base ternaria.
7. Si: )b()a()65( 23;2b4;ab3
están correctamente escritos,
hallar: a + b + c
8. Hallar: )b()a()65( 23;2b4;ab3
9. Hallar: (a + b + c); si se cumple:
bca)1a)(1a( )3( =−+
10. Al mayor número de dos cifras de la base cuaternaria, transformarlo a la base
nonaria. Dar la suma de sus cifras (base nonaria).
PROPIEDADES DE LOS NÚMEROS
11. Si: A = cantidad de divisores de 80.
B = suma de los tres primeros números primos de 2 cifras.
hallar: A + B
12. Si: A = 27 × 12 × 5 → _____________
B = 16 × 24 → _____________
C = 32 × 18 → _____________
hallar: CD
(A)
+ CD
(B)
+ CD
(C)
13. Si el siguiente número b7843 es divisible por 9. Calcular el valor de b
2
.
COLEGIO TRILCE Página 53

54. ARITMETICA
14. Siendo: M = {x/x es divisor de 12} y N = {x/x es divisor de 18}; hallar la suma de los
elementos en: M ∩ N.
15. Se tienen los siguientes conjuntos:
A = {x/x es múltiplo de 4; x ∈ N};
B = {x/x ∈ N; x es múltiplo de 7}
hallar cuántos elementos tiene A ∩ B, si todos son de 2 cifras.
CRITERIOS DE DIVISIBILIDAD
16. Restas al año de tu nacimiento la suma de las cuatro cifras que lo componen. ¿El
resultado obtenido es múltiplo de 9? ¿Por qué?
17. Hallar a + b, si: 195by17a3
ºº
+=+= .
18. Hallar la suma de valores de a, si:
º
2nnma2 = .
19. Calcular la suma entre el mayor y el menor valor que puede tomar x en:
º
321x4 =
20. Hallar la suma de valores de a, si:
º
42a29 = .
COLEGIO TRILCE Página 54