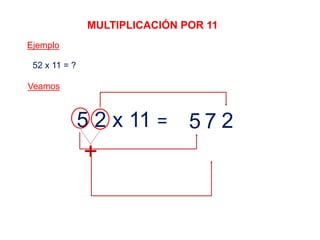
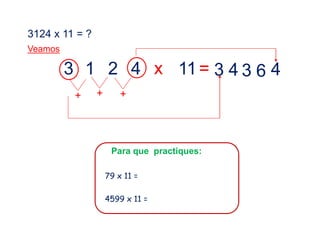
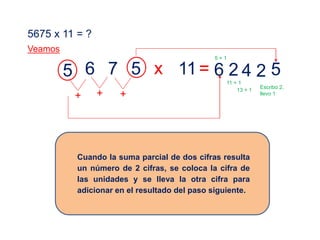
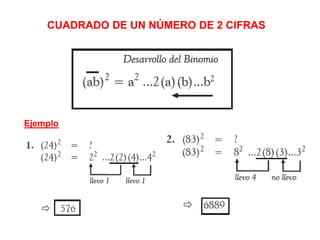
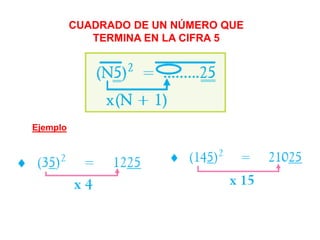
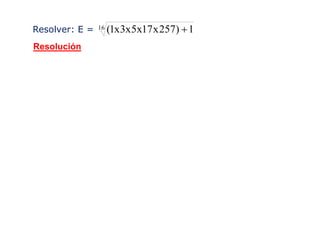
El documento presenta varios métodos y procedimientos para realizar operaciones aritméticas como multiplicaciones, divisiones, cuadrados y hallar cifras terminales. Explica cómo multiplicar por números como 5, 25, 11 y cómo dividir por 5. También cubre temas como el complemento aritmético y sus usos, cuadrados de números de una o dos cifras, y hallar cifras terminales de operaciones. El objetivo es desarrollar habilidades operativas para resolver problemas de manera más simple.

1. Al niño “Mayorcito” se le pideque
obtengacomorespuesta6 en cada
fila,utilizandolas4 operaciones
fundamentales;si sólopuede
utilizarraíces cuadradas , mas
no otrasraíces.
)(
¿Cuántasraícescuadradascree
ustedque el niñoutilizarácomo
mínimo?
999
888
777
666
555
6444
6333
6222



Respuesta : ....................

2. Como usted notaráel niño “Mayorcito”tiene que utilizar sus
habilidades aritméticas con un razonamiento que le permita resolver
el desafío.
En consecuencia el capítulo que desarrollamos ahora, titulado como
"HabilidadOperativa" consisteen desarrollarproblemas aritméticos,
algebraicos, geométricos, que aparentemente son operativos;pero con
ingenio y habilidad en las operaciones, se podrá resolver de manera
más simple y menos operativa.

3. Prof. Jenner Huamán Callirgos

4. MULTIPLICACIÓN POR 5
Deduzcamos el procedimiento a partir de un ejemplo
426 x 5 =?
426 x 5 = 426 x (
10
2
)
Veamos
=
4260
2
= 2130
23 x 5 =
2
230
= 115
Más ejemplos
976 x 5 =
2
9760
= 4880
Para multiplicar por 5, al
número se le agrega un
cero a su derecha y el
resultado se divide entre 2.
Para que practiques:
648 x 5 =
9737 x 5 =

5. MULTIPLICACIÓN POR 25
Deduzcamos el procedimiento a partir de un ejemplo
24 x 25 =?
24 x 25 = 24 x (
100
4
)
Veamos
=
2400
4
= 600
72 x 25 = = 1800
Más ejemplos
229 x 25 =
4
22900
= 5725
Para multiplicar por 25, al
número se le agrega dos
ceros a su derecha y el
resultado se divide entre 4.
Para que practiques:
124 x 25 =
645 x 25 =
4
7200

6. DIVISIÓN POR 5
Deduzcamos el procedimiento a partir de un ejemplo
Veamos
= 77
Más ejemplos
= 6428
Para dividir por 5, al número
se le multiplica por 2 y el
resultado se divide entre 10,
es decir, se cancela un cero
o se corre la coma decimal
un lugar hacia la izquierda.
Para que practiques:
8125 : 5 =
94540 : 5 =
135 𝑥 2
5 𝑥 2
=
270
10
= 27
135
5
=?
10
770
10
2385
5
385

x
10
64280
10
2x32140
5
32140


7. MULTIPLICACIÓN POR 11
52 x 11 = ?
Ejemplo
Veamos
5 2 x 11 = 2
+
75

8. 3124 x 11 = ?
Veamos
3 1 2 4 x 11= 463
+
43
++
Para que practiques:
79 x 11 =
4599 x 11 =

9. 5675 x 11 = ?
Veamos
5 6 7 5 x 11= 524
+
26
++
Cuando la suma parcial de dos cifras resulta
un número de 2 cifras, se coloca la cifra de
las unidades y se lleva la otra cifra para
adicionar en el resultado del paso siguiente.
Escribo 2,
llevo 1
13 + 1
11 + 1
5 + 1

10. MULTIPLICACIÓN POR 9; 99; 999; 9999; …
Deduzcamos el procedimiento a partir de un ejemplo
347 x 99 = 347(100 – 1) = 34700 – 347 = 34353
Para multiplicar cualquier número natural (N)
por otro número natural que está formado
íntegramente por cifras 9, al otro número (N)
hay que agregarle a su derecha tantos ceros
como cifras nueves hay, y al número que
resultare le restamos el mismo número (N).

11. Es decir:
N x 999 … 99 =
“n” cifras
N000… 00 - N
“n” cifras
N representa a cualquier número natural.
Ejemplos
123 x 99 = 12300 – 123 = 12177
746 x 9999 = 7460000 – 746 = 7459254

12. Para que practiques:
87 x 99 =
23 x 9999 =
501 x 999 =
1007 x 99999 =

13. MULTIPLICACIÓN DE 2 NÚMEROS DE 2
CIFRAS CADA UNO
21 X 14 = ?
Veamos
Deduzcamos el procedimiento a partir de un ejemplo
2 1 x
1 4
4
Producto de las
unidades (4x1)
Suma de los productos
en aspa(4x2) + (1x1)
9
Producto de las
cifras de las
decenas(2x1)
2

14. Para que practiques:
34 x 46 =
53 x 67 =
87 x 77 =
98 x 93 =
Si en una o en más de las operaciones parciales
resulta un número mayor 9, dejamos la cifra de las
unidades y llevamos las cifras restantes para la
siguiente operación.

15. EMPLEO DELCOMPLEMENTO
ARITMÉTICO(C.A.)
¿Qué es el complemento aritmético?
Se denomina complemento aritmético (C.A) de un número natural a la
cantidad que le falta a dicho número para ser igual a una unidad del
orden inmediato superior.
Ejemplo
Hallar el C.A. de
a) 748
b) 4578
Resolución
a) C.A(748) =1000 – 748 = 252
b) C.A(4578) =10000 – 4578 = 5422
En general:
C.A(N) = 10K - N
K  Número de cifras de “N”

16. Regla Práctica: Para hallar el
complemento aritmético de
un número, a partir de su mayor
orden se restan las cifras
de 9 y a la última cifra
significativa de 10; si hay ceros
al final éstos permanecen en el
CA.
Ejemplo:

01
9
310468

CA( ) = 895317
CA( ) = 765500

005234
01
9 
  )d10)(c9)(b9)(a9(abcd C A =
Complementos Aritméticos en
Otras Bases
 C A(34(7)) = 72 – 34(7)
 C A (429(11)) = 113 – 429(11)
 C A (7251(8)) = 84 – 7251(8)
Método Práctico:
En General:
C.A (N(B)) = )B(
K
)B(
N10 
K: números de cifras de “N”

17. Ejemplo
Utilicemos el C.A. para calcular algunas multiplicaciones. Los factores
son muy cercanos a una potencia de diez.
Calcula el resultado al multiplicar: 992 x 991
1º Paso
Calculamos los C.A. y los
multiplicamos. Al resultado le
hemos colocado un cero en el
lugar mostrado para que su
número de cifras sea igual al de
cada uno de los Factores.
992 x 991=
8 9x
…….072
2º Paso
Restamos de uno de los
factores el C.A. del otro
factor. Podríamos tomar por
ejemplo el factor 992 y
restarle 9(que es el C.A. de
991)
992 x 991= 072
8 9
El producto será: 983072
983

18. Ejemplo
Calcula la suma de las cifras del resultado de: 999987 x 999993
1º Paso
999987 x 999993 =
13 7x
…….000091
Al resultado le colocamos 4 ceros para que
su número de cifras sea igual al de cada
uno de los factores.
2º Paso
999987 x 999993 =
7
999980000091
La suma de cifras será:
9+9+9+9+8+9+1 = 54

19. CUADRADO DE UN NÚMERO DE 2 CIFRAS
Ejemplo

20. CUADRADO DE UN NÚMERO
CUALQUIERA
(N)2 = (N – a)(N + a) + a2
Donde “a” es el C.A. para ser un múltiplo de 10 una unidad inmediata
superior o inferior.
Ejemplo
(106)2 = (106 – 6)(106 + 6) + 62
= (100)(112) + 36
= 11200 + 36
= 11236
(108)2 = (108 – 8)(108 + 8) + 82
= (100)(116) + 64
= 11600 + 64
= 11664

21. CUADRADO DE UN NÚMERO QUE
TERMINA EN LA CIFRA 5
Ejemplo

22. Con decimales:
(85)2 =
(34)2 =
(52)2 =
(86)2 =
(93)2 =
(235)2 =
(555)2 =
(1005)2 =

23. Se llama así a la cifra de las unidades, después
de efectuar diferentes operaciones, lo cual sólo
se realiza con las cifras de las unidades.
CIFRAS TERMINALES

24. Para números que terminen en 0, 1, 5 y 6
(...0)n = ...0 (...5)n = ...5
(...1)n = ...1 (...6)n = ...6
Donde n  Z+

25. Para números que terminan en 4 y 9
(...4)impar = ...4 (...9)impar = ...9
(...4)par = ...6 (...9)par = ...1
Aquí notaremos que la última cifra del desarrollo dependerá de la
naturaleza par o impar.
(...4)²=(...4)(...4)=....6
(...4)3=(...4)(...4)(...4)= ....4
(...4)4=(...4)(...4)(...4)(...4)= ....6
(...4)5=(...4)(...4)(...4)(...4)(...4)=...4
(...9)²=(...9)(...9)=....1
(...9)3=(...9)(...9)(...9)= ....9
(...9)4=(...9)(...9)(...9)(...9)= ....1
(...9)5=(...9)(...9)(...9)(...9)(...9)=...9

26. Para números que terminan en 2, 3, 7 y 8
En estos casos dividiremos el exponente entre 4 y si el residuo es 1; 2
ó 3 la cifra terminal de la base se multiplica dicha cantidad de veces;
pero si la división es exacta entonces la cifra terminal se multiplica por
si misma 4 veces.
Observación
Sólo es necesario dividir las 2 últimas cifras del exponente.
Hallar la cifra terminal de A = (2143)4375
Ejemplo
Resolución
* A = (2143)4375 = (...3)75
Dividiendo:
75 4
18
3  residuo  la cifra terminal (...3)
se repite 3 veces
35
A = (...3) (...3) (...3) = ...7
Respuesta.- A termina en cifra 7
3 veces

27. Hallar la cifra terminal de B = (3148)7473
B = (3148)7473 = (...8)73
Resolución
Dividiendo:
73 4
1833
1  residuo  la cifra terminal (...8)
se repite 1 veces
B = (...8) = ...8
1 vez
Hallar la cifra terminal de C = (31427)2148
Resolución
C = (31427)2148 = (...7)48
48 4
1208
0  residuo  la cifra terminal (...7)
se repite 4 veces
Dividiendo: C = (...7) (...7) (...7) (...7) =...1
Respuesta.- B termina en cifra 8
Respuesta.- C termina en cifra 1

28. “El queaprende y aprende y no practica lo que aprende, es como
el que ara y ara la tierra y no siembra”
Anónimo

30.   MAXIMOLO
MATEMATICOTORAZONAMIEN 129919 
Hallar la cifra terminal de:
E =
Resolución
Respuesta: 6

31. Hallar la cifra terminal de A = (21474)1217 + (32879)3146
Resolución
Respuesta: 5

32. Hallar la suma de las cifras del resultado:
1)10003)(10002)(10001)(10000( A =
Resolución
Respuesta: 5

33. Hallar el resultado de “P” si P = (999997) (999993)
Resolución

34. Resolver: E = 16 1)257x17x5x3x1( 
Resolución

35. En qué cifra termina A = 55 x 54 x 53 x 52 x … x 1
A) 3 B) 5 C) 7 D) 0 E) 1.
Resolución

36. Calcular: a + b si: ab......)x7x5x3x1(
factores2003
4

  
A) 16 B) 25 C) 7 D) 10 E) 8
Resolución

37. •En qué cifra termina: RM
)22MATEMATICA864MAMA( 
A) 2 B) 4 C) 6D) 8 E) 5
Resolución

38. Calcular la suma de cifras del resultado:
E = (12345678)2 – (12345676)2
A) 36 B) 39 C) 41 D) 52 E) 24
Resolución

39. 6
6
66
)yx()zy()zx( 666

•Si: x – y = y – z = , Calcular el valor de:
A) 6 B) 16 C) 26 D) 36 E) N.A.
A =
Resolución

40. Si: (x + y + z + w)2 = 4(x + z) (y + w)
Calcular: M =
wzyx wzyx 33 33
3
Resolución

41. •Hallar el resultado de:
1414
4242
180180180
540540540
121212
363636

A) 6 B) 9 C) 12 D) 15 E) N.A.
Resolución

42. Si a + b + c = 0; a ≠ b ≠ c
Halle:
𝑀 =
3 𝑎 + 𝑏 𝑎 + 𝑐 𝑏 + 𝑐 + 3𝑎𝑏𝑐
𝑎5 + 𝑏5 + 𝑐5 + 𝑎9 + 𝑏9 + 𝑐9
A) 1 B) 0 C) 6 D) 2 E) 1/2

43. Si 𝐾𝐸𝑁𝐴𝑅 𝑥 99999 = … … . . 12345
Halle: (K + A + R + E +N)
A) 28 B) 29 C) 30 D) 31 E) 40

44. Resuelve:
𝐴 = [
1984 2016 +256
959 1041 +1681
]5
A) 32 B) 64 C) 128 D) 256 E) 1024

45. Si (+)(+) = (-)(-),
Calcule el valor de:
𝐴 = [
𝐸𝑁𝐸𝑅𝑂
𝐸𝑅𝐴
+
𝐷𝐼𝑁𝐸𝑅𝑂
𝐷𝐼𝑅𝐴
+
𝑀𝐴𝑆𝐴
𝐴𝑀𝐸𝑁𝑂𝑆
]5
A) 81 B) 64 C) 246 D) 0 E) 243

46. Si:
𝑏320 + 𝑏320 + 𝑏320 + 𝑏320 + … + 𝑏320 = 8181
81 veces
Halle:
𝐸 = 𝑏 − 1 𝑏−1 𝑏−1
A) 8 B) 16 C) 32 D) 4 E) 3